 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1401 | Gradito: |
Leggi anche appunti:Concetto dÌ segnaleCONCETTO DÌ SEGNALE Segnale: Messaggio che ha contenuto informativo decodificabile Risoluzione di una forma differenziale esattaRisoluzione di una forma differenziale esatta Consideriamo la funzione Area del trapezoideArea del trapezoide Con il calcolo dell'integrale vogliamo illustrare |
 |
 |
SERIE DI FOURIER
DEFINIZIONE
Consideriamo una funzione y=f(x) periodica in un periodo T=2p e si supponga che sia continua nell' intervallo [-p p] o, al più, dotata di punti di discontinuità di 1° o 3° specie nell'intervallo [-p p]. Se sussistono queste due condizioni la funzione y=f(x) è integrabile nell'intervallo [-p p] e sono integrabili (nello stesso intervallo) anche le seguenti due funzioni:
Se tutte le condizioni sono verificate allora possiamo definire la seguente serie come la serie di fourier della funzione f(x):
![]()
dove a0, ak, bk sono i coefficienti della serie di fourier
il valore di tali coefficienti sono dati dalle seguenti formule:
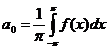


Stabiliti i valori dei coefficienti è semplice scrivere la serie di fourier, però bisogna tener conto che la serie potrebbe non convergere e, se converge, potrebbe non convergere proprio per y=f(x). A tale proposito sussiste ilseguente teorema:
Teorema di Dirichlet
data una funzione y=f(x) periodica con T=2p. Se f(x) ha nell'intervallo [-p p] un numero finito di punti di discontinuità di 1° e 3° specie, e se l'intervallo può essere suddiviso in un numero finito di intervalli parziali allora la serie di Fourier converge per qualsiasi valore di x, e precisamente:
Se f(x) è continua per qualsiasi valore di x, la sua serie di fourier converge a f(x) per qualunque x;
Se x0 è un punto di dicontinuità di 1° specie allora la serie di fourier converge a

![]() ;
;
Se x0 è un punto di dicontinuità di 3° specie allora la serie di fourier converge a
![]() .
.
N.B. Per quanto riguarda il calcolo dei coefficienti si ricorda che trattandosi di calcolo di integrali definiti in un intervallo simmetrico.
.se f(x) = funzione pari  sviluppo di
soli coseni;
sviluppo di
soli coseni;
.se f(x) = funzione dispari  sviluppo di soli
seni;
sviluppo di soli
seni;
.se f(x) = funzione né pari, né
dispari sviluppo di
seni e coseni;
sviluppo di
seni e coseni;
 |
| Appunti su: appunti serie di fourier, |
|
| Appunti Statistica |  |
| Tesine Contabilita |  |
| Lezioni Fisica |  |