 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2212 | Gradito: |
Leggi anche appunti:LOBACEVSKIJ E BOLYAI: una rivelazione inaccettabileLOBACEVSKIJ E BOLYAI: una rivelazione inaccettabile Degli altri due uomini Un nuovo postulato delle paralleleUN NUOVO POSTULATO delle parallele Una trentina d'anni dopo la pubblicazione Matematica. . . mente - tesinaMATEMATICA. . . MENTE Come |
 |
 |
PROCESSO STOCASTICO
Cos'è un processo stocastico e a che serve
I dati a cui vengono applicate le tecniche inferenziali possono essere di due tipi: cross-section, nel caso in cui le osservazioni di cui disponiamo siano relative ad individui diversi, oppure serie storiche, quando ciò che abbiamo sono osservazioni, su una o più grandezze, protratte nel tempo.
Il caso delle serie storiche, rispetto a quello dei dati cross-section, presenta una differenza concettuale di base: questa differenza consiste nel fatto che il tempo ha una direzione, e quindi "esiste la storia".
In un contesto di serie storiche, infatti, la naturale tendenza di molti fenomeni ad evolversi in modo più o meno "regolare" porta a pensare che il dato rilevato in un dato istante t sia più simile a quello rilevato all'istante t-1 piuttosto che in epoche distanti; si può dire, in un certo senso, che la serie storica che analizziamo ha "memoria di sé": questa caratteristica è generalmente indicata col nome di persistenza (istèresi, o isterèsi, per gli economisti) e differenzia profondamente i campioni di serie storiche da quelli cross-section, perché nei primi l'ordine dei dati ha un'importanza fondamentale, mentre nei secondi esso è del tutto irrilevante.
Lo strumento che utilizziamo per far fronte all'esigenza di trovare una metafora probabilistica per le serie storiche osservate è il processo stocastico. Una definizione di processo stocastico non rigorosa, ma intuitiva e sostanzialmente corretta può essere la seguente: un processo stocastico è un vettore aleatorio di dimensione infinita.
Le proprietà dei processi stocastici fanno riferimento ai processi stocastici come strutture probabilistiche. Quando però vogliamo utilizzare queste strutture come base per procedure inferenziali, si aprono due problemi (i seguenti):
![]() se quella che osservo
(peraltro non nella sua interezza) è una sola realizzazione delle molte
possibili, la possibilità "logica" di
fare "inferenza sul processo" non può essere data per scontata; infatti, non
c'è modo di dire quali caratteristiche della serie osservata sono specifiche di
quella realizzazione e quali invece si ripresenterebbero anche osservandone
altre.
se quella che osservo
(peraltro non nella sua interezza) è una sola realizzazione delle molte
possibili, la possibilità "logica" di
fare "inferenza sul processo" non può essere data per scontata; infatti, non
c'è modo di dire quali caratteristiche della serie osservata sono specifiche di
quella realizzazione e quali invece si ripresenterebbero anche osservandone
altre.
![]() se anche fosse
possibile usare una sola realizzazione per fare "inferenza sulle
caratteristiche del processo", è necessario che esso sia stabile nel tempo,
cioè che i suoi connotati probabilistici permangano invariati, per lo meno
all'interno del mio intervallo di osservazione.
se anche fosse
possibile usare una sola realizzazione per fare "inferenza sulle
caratteristiche del processo", è necessario che esso sia stabile nel tempo,
cioè che i suoi connotati probabilistici permangano invariati, per lo meno
all'interno del mio intervallo di osservazione.
Ebbene, queste due questioni conducono alla definizione di due (ulteriori) proprietà che i processi stocastici possono avere o non avere (e che sono i seguenti)
Stazionarietà
Si parla di processo stocastico stazionario in due sensi: stazionarietà forte (anche detta stretta) e stazionarietà debole.
Per definire la stazionarietà forte, prendiamo
in esame un sottoinsieme qualunque delle variabili casuali che compongono il
processo (queste non devono necessariamente essere consecutive, ma per aiutare
l'intuizione, facciamo finta che lo siano). Consideriamo perciò una "finestra"
aperta sul processo di ampiezza k (la
finestra), ossia un sottoinsieme del tipo
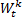 = ( xt,.,xt+k-1 ).
Questa è naturalmente una variabile casuale a k dimensioni, con una sua funzione di densità che, in generale, può
dipendere da t. Se però ciò non
accade, allora la distribuzione di
= ( xt,.,xt+k-1 ).
Questa è naturalmente una variabile casuale a k dimensioni, con una sua funzione di densità che, in generale, può
dipendere da t. Se però ciò non
accade, allora la distribuzione di
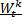 è uguale a quella di
è uguale a quella di
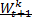
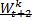 e così via. Ebbene, siamo in presenza di
stazionarietà forte quando questa invarianza vale per qualsiasi k. In altri termini, quando un processo
è stazionario in senso forte le caratteristiche distribuzionali di tutte le
marginali rimangono costanti al passare del tempo.
e così via. Ebbene, siamo in presenza di
stazionarietà forte quando questa invarianza vale per qualsiasi k. In altri termini, quando un processo
è stazionario in senso forte le caratteristiche distribuzionali di tutte le
marginali rimangono costanti al passare del tempo.
La stazionarietà debole, invece, riguarda solo "finestre"
di ampiezza 2 (k=2): si ha
stazionarietà debole se tutte le variabili casuali doppie
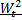 = ( xt,
xt ), hanno momenti primi e secondi COSTANTI "nel
tempo" (è per questo motivo che la stazionarietà debole viene anche definita
stazionarietà in covarianza) ([1]).
= ( xt,
xt ), hanno momenti primi e secondi COSTANTI "nel
tempo" (è per questo motivo che la stazionarietà debole viene anche definita
stazionarietà in covarianza) ([1]).
A dispetto dei nomi, una definizione non implica l'altra; ad esempio, un processo può essere stazionario in senso forte ma non possedere momenti; viceversa, la costanza nel tempo dei momenti (stazionarietà debole) non implica che le varie marginali abbiano la stessa distribuzione (stazionarietà forte). In un caso, tuttavia, le due definizioni coincidono: questo caso - che è particolarmente importante per le applicazioni pratiche - è quello in cui il processo è "gaussiano", ossia quando la distribuzione congiunta di un qualunque sottoinsieme di elementi del processo è una normale multivariata: se un processo è gaussiano, stabilire che è stazionario in senso debole equivale a stabilire la stazionarietà forte. Data la pervasività dei processi gaussiani nelle applicazioni ai dati, da un punto di vista operativo si adotta generalmente la definizione di stazionarietà debole, e quando si parla di stazionarietà senza aggettivi, è appunto a questa che ci si riferisce.
Ergodicità
L'ergodicità è una condizione che limita la memoria del processo: un processo NON ERGODICO è un processo che ha caratteristiche di PERSISTENZA così accentuate da far sì che un segmento del processo, per quanto lungo, sia insufficiente a dire alcunché sulle sue caratteristiche distributive.
In un processo ERGODICO, al contrario, la memoria del processo è debole su lunghi orizzonti e all'aumentare dell'ampiezza del campione aumenta in modo significativo anche l'informazione in nostro possesso.
In altre parole si può dire che un processo è ergodico se eventi "molto" lontani fra loro possono essere considerati "virtualmente" indipendenti: osservando il processo per un lasso di tempo "abbastanza" lungo, è possibile osservare "quasi tutte" le sottosequenze che il processo è in grado di generare. Di conseguenza, se un processo è ergodico, è possibile (almeno in linea di principio) usare le informazioni contenute nel suo svolgimento nel tempo per "inferirne" le caratteristiche. Esiste un teorema (detto appunto "teorema ergodico") che dice che, se un processo è ergodico, l'osservazione di una sua realizzazione abbastanza lunga è equivalente, ai fini "inferenziali", all'osservazione di un gran numero di realizzazioni.
In linea generale, si può dire che L'"INFERENZA" È POSSIBILE SOLO SE IL PROCESSO STOCASTICO CHE SI STA STUDIANDO È "STAZIONARIO" ED "ERGODICO".
DECOMPOSIZIONE DI UNA SERIE STORICA
Uno degli scopi fondamentali dell'analisi classica delle serie temporali è quello di scomporre la serie nelle sue componenti, isolandole per poterle studiare meglio. Inoltre, per poter applicare l'approccio stocastico (modelli AR, MA, ARIMA) alle serie storiche è quasi sempre necessario eliminare il "trend" e la "stagionalità" al fine di avere un processo "stazionario".
Le componenti di una serie storica di solito sono le seguenti: trend (Tt), stagionalità (Ct), ciclo(St), residua o erratica (Et
Esse possono essere legate tra loro in modo additivo:
Yt Tt + Ct + St + Et
oppure in modo moltiplicativo:
Yt Tt x Ct x St x Et
Un modello di tipo moltiplicativo può essere facilmente trasformato in un modello additivo usando l'operatore logaritmo:
log(Yt = log(Tt)+ log(Ct)+ log(St)+ log(Et
Stima delle componenti
Medie mobili, differenze dei termini
Oltre al metodo analitico per la stima del trend (Tt), ci sono metodi più elementari anche se meno raffinati per "detrendizzare" una serie temporale: la perequazione meccanica con medie mobili e l'applicazione dell'operatore differenza.
Medie mobili. Nel caso delle medie mobili si pone il problema dell'esatta determinazione del numero dei termini da usare.
In genere il trend può essere stimato con un'opportuna ponderazione dei valori della serie:
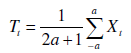
Operatore differenza. Un ulteriore metodo per eliminare il trend è quello di operare sulle differenze tra i termini (o i logaritmi dei termini in caso di modello moltiplicativo) della serie storica: le differenze del primo ordine rimuovono un trend lineare, quelle del secondo ordine un trend parabolico, quelle di ordine k rimuovono un trend polinomiale di grado k:
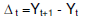
Livellamento esponenziale con il metodo di Holt-Winters
Il livellamento esponenziale è un metodo che può aiutare a descrivere l'andamento di una serie storica e soprattutto è un utile strumento per effettuare delle previsioni.
Metodo analitico
L'approccio più semplice della decomposizione classica, utile a titolo introduttivo, è basato sul modello:
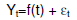
in cui f(t) è una funzione del tempo che descrive trend (Tt) e stagionalità (Ct) in modo semplice. In particolare nel caso di un modello di tipo additivo, come nella nostra esemplificazione pratica:
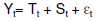
con et ~ NID (0,2), ovvero supponendo che gli errori siano distribuiti normalmente con media zero e varianza costante (omoschedasticità) e siano tra loro indipendenti. Sono le ipotesi di base della regressione lineare che verranno verificate tramite appositi tests di specificazione del modello.
TEST DI SPECIFICAZIONE
Nel paragrafo precedente si è supposto che la componente erratica (t) fosse distribuita normalmente con media pari a zero, varianza costante (omoschedasticità) e che non vi fosse autocorrelazione.
Tali ipotesi alla base del modello vanno opportunamente verificate con opportuni test statistici detti tests di specificazione del modello ([2]).
Verifica sul valore della media degli errori
In primo luogo occorre verificare che la media dei residui non sia significativamente diversa da zero. Occorre effettuare il test t. Se n è il numero di osservazioni della serie allora la media degli errori osservati è:
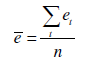
e la varianza campionaria corretta:
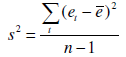
Ebbene, il test da effettuare è:
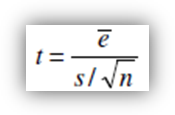
che si distribuisce come una t di Student con n-1 gradi di libertà.
Test di normalità degli errori
Prima di procedere a verificare che i residui si distribuiscano secondo una v.c. normale, andiamo ad esaminare i residui al fine di individuare dei valori "anomali".
È preferibile operare sui residui standardizzati
Test di Wilk-Shapiro
Il test di Shapiro-Wilk è considerato in letteratura uno dei test più potenti per la verifica della normalità, soprattutto per piccoli campioni.
La verifica della normalità avviene confrontando due stimatori alternativi della varianza 2: uno stimatore non parametrico basato sulla combinazione lineare ottimale della statistica d'ordine di una variabile aleatoria normale al numeratore, e il consueto stimatore parametrico, ossia la varianza campionaria, al denominatore.
I pesi per la combinazione lineare sono disponibili su apposite tavole. La statistica W può essere interpretata come il quadrato del coefficiente di correlazione in un diagramma quantile-quantile.
Test di Breusch-Pagan per omoschedasticità
Il test di Breusch-Pagan, largamente utilizzato per verificare l'ipotesi di omoschedasticità (varianza dei residui costante), applica ai residui gli stessi concetti della regressione lineare.
Esso è valido per grandi campioni, assume che gli errori siano indipendenti e normalmente distribuiti e che la loro varianza (t) sia funzione lineare del tempo t secondo:
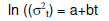
Ciò implica che la varianza aumenta o diminuisce al variare di t, a seconda del segno di b.
Se si ha l'omoschedasticità, si realizza l'ipotesi nulla:
Contro l'ipotesi alternativa (bidirezionale) b ≠ 0
Test di autocorrelazione
Si può avere un fenomeno di autocorrelazione temporale (i residui NON sono tra loro indipendenti) a causa dell'inerzia o stabilità dei valori osservati, per cui ogni valore è influenzato da quello precedente e determina in parte rilevante quello successivo.
Esistono diversi test statistici per saggiare la presenza di una correlazione seriale dei residui di una serie storica. In questa sede si farà riferimento ai test di Box-Pierce, Ljung-Box Tests e Durbin-Watson.
Uso del correlogramma
Un modo abbastanza semplice per vedere se una serie presenza autocorrelazione è quella di tracciarne il correlogramma. In caso di assenza di autocorrelazione la distribuzione asintotica della stima del coefficiente di autocorrelazione è di tipo normale ed avremo una banda di confidenza del tipo:
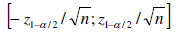
(Tracciando il correlogramma dei residui standardizzati) valori esterni a tale intervallo indicano la presenza di autocorrelazione significativa.
Test di Ljung-Box e di Box-Pierce
Ljung-Box. Una statistica che può essere utilizzata per verificare l'assenza di autocorrelazione è una opportuna combinazione lineare dei coefficienti di autocorrelazione dei residui r(t):
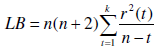
dove k è un intero prescelto.
Se è vera l'ipotesi nulla (assenza di autocorrelazione) la statistica LB si distribuisce asintoticamente secondo una variabile casuale Chi-Quadro con k gradi di libertà.
Box-Pierce. Un test analogo a quello di Ljung-Box è quello che si basa sulla statistica proposta da Box-Pierce:
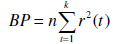
Le due statistiche differiscono semplicemente per il diverso sistema di ponderazione adoperato, ma asintoticamente hanno la medesima distribuzione. Si dimostra, tuttavia, che LB ha una convergenza più rapida alla distribuzione asintotica e, per tale motivo, risulta preferibile al test di Box-Pierce.
Test di di Durbin-Watson
Un ulteriore modalità per valutare l'esistenza di autocorrelazione tra i residui è rappresentata dal test di Durbin-Watson, che saggia l'ipotesi nulla di assenza di autocorrelazione tra i residui.
È un test di solito adoperato per la verifica sui residui della regressione, ma è anche applicabile ai residui di una serie storica.
La statistica test è:
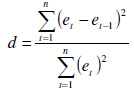
Grafico di auto dispersione
Un ulteriore metodo (grafico) per verificare se una serie storica presenta autocorrelazione è quello di tracciare il grafico di dispersione tra la serie originaria e la stessa serie ritardata di un certo lag. Tale grafico è detto spesso di auto dispersione.
I processi ARMA
I processi ARMA costituiscono la famiglia di processi stocastici di gran lunga più utilizzati in econometria. Questa scelta ha ragioni teoriche e ragioni pratiche, che saranno illustrate nel seguito. Prima di analizzare le caratteristiche principali di tali processi, tuttavia, sono necessarie alcune definizioni di base, che formano l'oggetto dei prossimi paragrafi.
L'operatore ritardo
Tanto i processi stocastici che le serie storiche sono, in buona sostanza, sequenze di numeri. Capiterà molto spesso di dover manipolare tali sequenze, e lo faremo per mezzo di appositi operatori. L'operatore ritardo viene generalmente indicato con la lettera L nella letteratura econometrica; è un operatore che si applica a sequenze di numeri, e trasforma una sequenza (stocastica o no) xt in un altra sequenza che ha la curiosa caratteristica di avere gli stessi valori di xt, ma sfalsati di un periodo.
Se applicato ad una costante, la lascia invariata.
In formule:
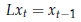
L'applicazione ripetuta n volte di L viene indicata con la scrittura Ln, e quindi si ha:
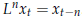
Per convenzione si pone L
L'operatore L è un operatore lineare, nel senso che, se a e b sono costanti, si ha:
L(axt + b = aLxt + b = axt-1 + b.
La caratteristica più divertente dell'operatore L è che le sue proprietà appena enunciate permettono, in molte circostanze, di manipolarlo algebricamente come se fosse un numero.
Processi white noise
Il white noise (rumore bianco) è il processo stocastico più semplice che si può immaginare: infatti, è un processo che possiede momenti (almeno) fino al secondo ordine; essi sono costanti nel tempo (quindi il processo è "stazionario"), ma non danno al processo alcuna "memoria" di sé. La stessa cosa si può dire in modo più formalizzato come segue: un processo white noise, il cui elemento t-esimo indicheremo con єt, presenta queste caratteristiche:
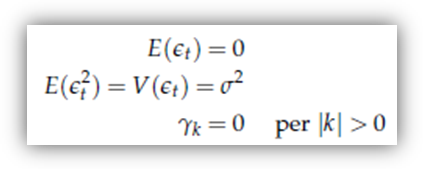
Un white noise è quindi, in sostanza, un processo composto di un numero infinito di variabili casuali a media zero e varianza costante; queste variabili casuali, inoltre, sono tutte incorrelate l'una all'altra.
A rigore, questo non significa che esse siano indipendenti. Se però si parla di white noise gaussiano, ossia di un white noise in cui la distribuzione congiunta di tutte le coppie (єt t+k) sia una normale bivariata, allora sì.
Un processo white noise, quindi, è un processo stocastico che non esibisce persistenza. In quanto tale, si potrebbe pensare che sia inadeguato a raggiungere lo scopo che ci eravamo prefissi nella premessa, cioè trovare una struttura probabilistica che possa servire da metafora per campioni di serie storiche che, invece, la persistenza ce l'hanno. Il passo in avanti decisivo, che vediamo nel prossimo paragrafo, sta nel considerare cosa succede applicando un polinomio nell'operatore ritardo ad un white noise.
Processi MA
Un processo MA, o processo a media mobile (MA sta appunto per Moving Average), è una sequenza di variabili casuali che può essere scritta nella forma
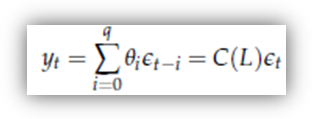
dove:
o C(L) è un polinomio di ordine q nell'operatore ritardo ([3])
e
o t è un white noise.
Generalmente, e senza perdita di generalità, si pone C(0) = θ0 = 1.
Se C(L) è un polinomio di grado q, si dice anche che yt è un processo MA(q), che si legge "processo MA di ordine q".
Esaminiamo i suoi momenti
![]() Per quanto riguarda il
momento primo, si ha
Per quanto riguarda il
momento primo, si ha
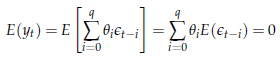
E quindi un processo MA ha media 0. A prima vista, si potrebbe pensare che questa caratteristica limiti fortemente l'applicabilità di processi MA a situazioni reali, visto che, in genere, non è detto che le serie storiche osservate oscillino intorno al valore 0. Tuttavia, la limitazione è più apparente che reale, visto che per ogni processo xt per cui E(xt t si può sempre definire un nuovo processo yt = xt t a media nulla (in questo semplice esempio il processo xt non è stazionario, secondo la definizione che ci siamo dati, ma il processo yt sì). Se yt è stazionario in covarianza, allora basta studiare yt e poi ri-aggiungere la media per avere xt
![]() Per
quanto riguarda la varianza, il fatto che il momento primo sia nullo ci
consente di scriverla come il momento secondo, ossia
Per
quanto riguarda la varianza, il fatto che il momento primo sia nullo ci
consente di scriverla come il momento secondo, ossia
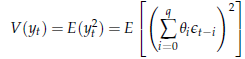
Sviluppando il quadrato, possiamo scomporre la somma in due parti distinte:
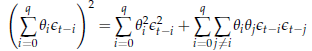
Dovrebbe essere ovvio, dalla proprietà del white noise, che il valore atteso della seconda sommatoria è nullo, cosicché
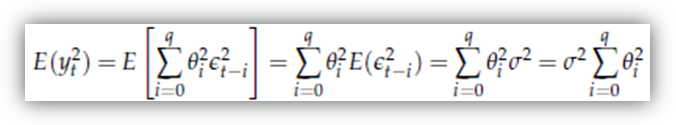
che ha valore finito se
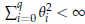
cosa sempre vera se q è finito.
![]() Infine, con un
ragionamento del tutto analogo perveniamo al calcolo delle autocovarianze:
l'autocovarianza di ordine k è data
da
Infine, con un
ragionamento del tutto analogo perveniamo al calcolo delle autocovarianze:
l'autocovarianza di ordine k è data
da
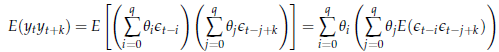
Sfruttando ancora le proprietà del white noise, si ha che
o E t-i t-j+k per j = i + k
e
o E t-i t-j+k in tutti gli altri casi,
cosicché l'espressione precedente si riduce a:
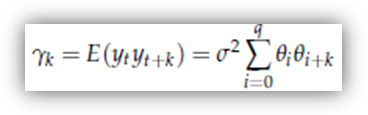
dove si intende che θi = 0 per i > q.
Si noti che:
l'espressione per la varianza è un caso particolare della formula precedente, ponendo k = 0;
per k > q, le autocovarianze sono nulle.
Un processo MA(q), quindi, è un processo ottenuto come combinazione di diversi elementi di uno stesso white noise che presenta delle caratteristiche di "persistenza" tanto più pronunciate quanto più alto è il suo ordine q.
Poniamoci ora un problema inferenziale: se volessimo rappresentare una certa serie storica come realizzazione di un processo MA(1), come potremmo utilizzare le statistiche calcolabili sulla serie per ricavare delle stime dei parametri del processo (in questo caso, il parametro θ)? Naturalmente, questo procedimento sarebbe sostenibile solo nel caso in cui la nostra serie avesse un correlogramma empirico con valori moderati per l'autocorrelazione di primo ordine e trascurabili per le altre. Se così fosse, potremmo anche fare un ragionamento del tipo: se il processo che ha generato i dati è effettivamente un MA(1), allora è stazionario ed ergodico, per cui l'autocorrelazione campionaria converge in probabilità a quella teorica. In formule:
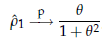
poiché
questa è una funzione continua di θ,
posso invertirla e trovare uno stimatore consistente di θ col metodo dei momenti, ossia trovare quel valore
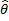 che soddisfa l'equazione
che soddisfa l'equazione
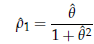
Si vede facilmente che la soluzione è
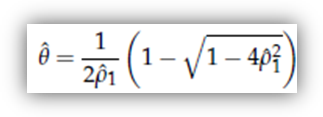
In
pratica, potremmo dire: visto che l'autocorrelazione campionaria è di (poniamo)
0.4, se sono convinto che il processo che ha generato i dati sia un MA(1),
allora scelgo quel valore di θ
tale per cui l'autocorrelazione teorica è anch'essa 0.4, ossia
 = 0.5. Naturalmente, questa strategia è
perfettamente giustificata nella misura in cui la serie abbia effettivamente le
caratteristiche di covarianza richieste, ossia una autocorrelazione di ordine 1
non troppo grande e autocorrelazioni successive trascurabili.
= 0.5. Naturalmente, questa strategia è
perfettamente giustificata nella misura in cui la serie abbia effettivamente le
caratteristiche di covarianza richieste, ossia una autocorrelazione di ordine 1
non troppo grande e autocorrelazioni successive trascurabili.
Ora, noi sappiamo che le cose non stanno sempre così (basta dare un'occhiata alle figure 1.2 e 1.4). È però vero che un processo MA di ordine superiore (q>1) ha autocovarianze più articolate, e quindi si può congetturare che la stessa strategia potrebbe essere percorribile, almeno in teoria, a condizione di specificare un ordine del polinomio C(L) abbastanza alto.
Facendo un passo più in là, ci si potrebbe chiedere se la congettura vale per qualunque struttura di autocovarianze. La risposta è nel mai abbastanza celebrato teorema di rappresentazione di Wold, di cui fornisco solo l'enunciato.
Teorema di rappresentazione di Wold. Dato un qualunque processo stocastico yt, stazionario "in covarianza" e a media 0, è sempre possibile trovare una successione (non necessariamente finita) di coefficienti θi tali per cui
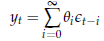
dove єt è un white noise.
Processi AR
Un'altra importante classe di processi è data dai processi AR (AutoRegressivi). Questi processi forniscono, in un certo senso, una rappresentazione più intuitiva di una serie "persistente" di quella dei processi MA, poiché l'idea è che il livello della serie al tempo t sia una funzione lineare dei propri valori passati, più un white noise. Il nome deriva appunto dal fatto che un modello AR somiglia molto ad un modello di regressione in cui le variabili esplicative sono i valori passati della variabile dipendente:
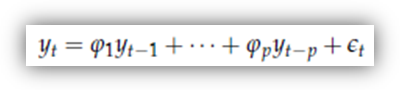
Non è ozioso notare che, in questo contesto, il white noise єt può essere interpretato in modo analogo al disturbo di un modello di regressione, cioè come la differenza fra yt e la sua media condizionale: in questo caso, le variabili casuali che costituiscono l'insieme di "condizionamento" sono semplicemente il passato di yt
I processi AR sono in un certo senso speculari ai processi MA perché, se un processo MA è un processo definito dall'applicazione di un polinomio nell'operatore L ad un white noise, un processo AR è definito come un processo l'applicazione al quale di un polinomio nell'operatore L produce un white noise. In simboli
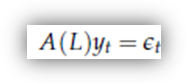
dove A(L) è il solito polinomio in L (di grado p)
con A(0) = 1
e
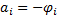 .
.
Per familiarizzare con questo tipo di processi, iniziamo col considerare il caso più semplice: quello in cui p = 1 - AR(1) - e il processo può essere scritto
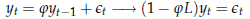
Quali sono le caratteristiche di questo processo? Tanto per cominciare, vediamo come sono fatti i suoi momenti.
![]() Momenti primi. I
momenti di un processo AR(1) possono essere ricavati in diversi modi: uno
piuttosto intuitivo è quello di supporre la stazionarietà del processo, e poi
derivare le conseguenze di questa ipotesi. Supponiamo quindi che il processo
abbia media costante μ.
Quest'ipotesi implica
Momenti primi. I
momenti di un processo AR(1) possono essere ricavati in diversi modi: uno
piuttosto intuitivo è quello di supporre la stazionarietà del processo, e poi
derivare le conseguenze di questa ipotesi. Supponiamo quindi che il processo
abbia media costante μ.
Quest'ipotesi implica
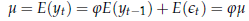
L'espressione precedente (com'è intuitivo) può essere vera in due casi:
o nel
caso μ = 0, nel qual caso è vera
per qualsiasi valore di
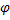
oppure
o nel
caso
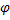 = 1, e allora l'espressione è vera per
qualsiasi valore di μ, e la
media del processo è indeterminata. In questo secondo caso si dice che il
processo presenta una radice unitaria (perché il valore di z per cui A(z) = 0 è appunto 1); l'analisi di questa
situazione, in cui accadono cose bizzarre, ha occupato pesantemente le menti
dei migliori econometrici e le pagine delle riviste scientifiche negli ultimi
vent'anni del XX secolo, e per molto tempo è stato considerato dagli economisti
applicati un terreno impervio. Noi non ne parleremo. Per il momento, escludiamo
dall'indagine i polinomi per cui A(1)
= 0. Ne consegue che (nei casi che analizziamo qui) il processo ha media 0 (μ = 0).
= 1, e allora l'espressione è vera per
qualsiasi valore di μ, e la
media del processo è indeterminata. In questo secondo caso si dice che il
processo presenta una radice unitaria (perché il valore di z per cui A(z) = 0 è appunto 1); l'analisi di questa
situazione, in cui accadono cose bizzarre, ha occupato pesantemente le menti
dei migliori econometrici e le pagine delle riviste scientifiche negli ultimi
vent'anni del XX secolo, e per molto tempo è stato considerato dagli economisti
applicati un terreno impervio. Noi non ne parleremo. Per il momento, escludiamo
dall'indagine i polinomi per cui A(1)
= 0. Ne consegue che (nei casi che analizziamo qui) il processo ha media 0 (μ = 0).
![]() Per quanto riguarda i momenti
secondi, procediamo come sopra; supponiamo che il white noise єt
abbia varianza pari a σ2.
Se indichiamo con V la varianza di yt,
e supponiamo che essa esista e sia costante nel tempo, avremo che
Per quanto riguarda i momenti
secondi, procediamo come sopra; supponiamo che il white noise єt
abbia varianza pari a σ2.
Se indichiamo con V la varianza di yt,
e supponiamo che essa esista e sia costante nel tempo, avremo che
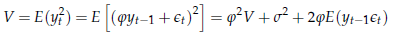
L'ultimo elemento della somma è 0, poiché yt- = C(L) єt- e quindi E(yt- t) è una combinazione lineare di autocovarianze di un white noise (tutte nulle per definizione). Se ne deduce che
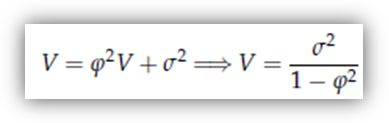
L'espressione
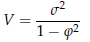
ci dice più di una cosa:
o in
primo luogo, ci dice che solo se │
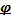 │<
1 ha senso parlare di varianza stabile nel tempo
│<
1 ha senso parlare di varianza stabile nel tempo
( per │
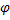 │≥
1 non vale più l'ultima eguaglianza: questa
condizione esclude quindi dal novero dei processi AR(1) stazionari non solo
quelli a radice unitaria, quindi quelli dove
│≥
1 non vale più l'ultima eguaglianza: questa
condizione esclude quindi dal novero dei processi AR(1) stazionari non solo
quelli a radice unitaria, quindi quelli dove
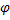 = 1, ma anche quelli a radice cosiddetta
esplosiva, │
= 1, ma anche quelli a radice cosiddetta
esplosiva, │
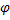 │>
1 );
│>
1 );
o la seconda considerazione nasce dal confronto di V, che è la varianza "non condizionale" di yt, con σ2, che è la varianza di yt xt
V
è sempre maggiore di σ2,
e la differenza è tanto maggiore quanto più
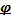 è vicino a 1 → tanto più "persistente" è
il processo, tanto più la sua varianza condizionale al proprio passato (σ2) sarà minore della
sua varianza non condizionale (V) →
vale a dire che la conoscenza del valore di yt
riduce l'incertezza sul valore di yt
quanto più "persistente" è la serie (com'e logico).
è vicino a 1 → tanto più "persistente" è
il processo, tanto più la sua varianza condizionale al proprio passato (σ2) sarà minore della
sua varianza non condizionale (V) →
vale a dire che la conoscenza del valore di yt
riduce l'incertezza sul valore di yt
quanto più "persistente" è la serie (com'e logico).
![]() Rimangono da vedere le
autocovarianze:
Rimangono da vedere le
autocovarianze:
o autocovarianza di ordine 0 = V (che conosciamo già)
o autocovarianza di ordine 1:
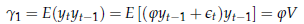
o e più in generale l'autocovarianza di ordine k
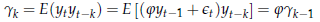
da cui si deduce che
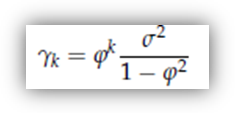
![]() Le autocorrelazioni
assumono in questo caso una forma molto semplice:
Le autocorrelazioni
assumono in questo caso una forma molto semplice:
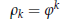
Anche
in questo caso è possibile dare un'interpretazione intuitiva del risultato: le
autocorrelazioni, che sono un indice della "memoria" del processo, sono tanto
più grandi (in valore assoluto), quanto più grande (in valore assoluto) è
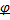 ,
confermando l'interpretazione di
,
confermando l'interpretazione di
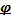 come parametro di "persistenza".
come parametro di "persistenza".
Applichiamo a questo white noise l'operatore:
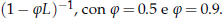
Anche
in questo caso, si nota un aumento delle caratteristiche di "persistenza"
all'aumentare del parametro (
 in questo caso), anche se qui la cosa è molto
più marcata.
in questo caso), anche se qui la cosa è molto
più marcata.
Come nel caso dei processi MA, è facile generalizzare i processi AR al caso di media non nulla. Il risultato è il seguente:
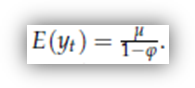
La generalizzazione al caso AR(p) è piuttosto noiosa dal punto di vista dei maneggi algebrici che sono necessari. Comunque il punto fondamentale è che un processo AR(p) è "stazionario" solo se │λj│< 1 per ogni j (le λj sono i reciproci delle radici di A(L).
Altri fatti interessanti sono che un processo AR(p):
![]() ha memoria infinita,
ma le autocorrelazioni decrescono al crescere di k in progressione geometrica;
ha memoria infinita,
ma le autocorrelazioni decrescono al crescere di k in progressione geometrica;
![]() nel caso di
"intercetta" diversa da 0, ha valore atteso
nel caso di
"intercetta" diversa da 0, ha valore atteso
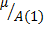
L'unico aspetto che vale la pena di sottolineare del caso in cui l'ordine del processo autoregressivo p sia maggiore di 1 - p>1 - è che processi AR(p) possono avere andamenti ciclici: in questo caso, il processo assume un andamento ciclico in cui l'ampiezza delle oscillazioni varia attorno ad un valore medio. Dovrebbe essere evidente che i processi di questo tipo sono i candidati naturali a modellare fenomeni economici caratterizzati da fasi cicliche.
Processi ARMA
La classe dei processi ARMA comprende sia i processi AR che i processi MA come caso particolare. Un processo ARMA(p, q) è infatti definito da
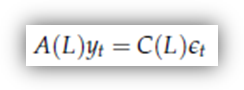
dove p è l'ordine del polinomio A(L) e q è l'ordine del polinomio C(L). Entrambi (p e q) sono numeri finiti.
I processi AR o MA sono quindi casi particolari (q = 0 e p = 0 rispettivamente).
Che senso ha studiare processi ARMA? In linea teorica, nessuna, visto che il teorema di rappresentazione di Wold ci dice che qualunque processo "stazionario" può essere rappresentato come un processo MA. Da un punto di vista pratico, tuttavia, c'è il problema che la rappresentazione di Wold è, in generale, INFINITA. Questo non è un problema a livello teorico, ma lo diventa nella pratica: la serie che osserviamo viene infatti pensata come realizzazione di un processo stocastico, i cui parametri sono i coefficienti dei polinomi nell'operatore L che ne determinano le caratteristiche di persistenza (più la varianza del white noise).
Se si considera una serie osservata come una realizzazione di un qualche processo stazionario, utilizzare un processo MA per riassumerne le caratteristiche di media e covarianza comporta quindi il problema inferenziale di stimare un numero potenzialmente INFINITO di parametri. Infatti, se pensiamo che yt sia rappresentabile in forma MA come
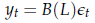
niente ci assicura che il polinomio B(L) non sia di ordine INFINITO.
L'esigenza di tener basso il numero dei parametri dei polinomi conduce, in certi casi, a lavorare con dei modelli noti come ARMA moltiplicativi, che si usano soprattutto per serie caratterizzate da persistenza stagionale, e che quindi sono anche conosciuti come ARMA stagionali, o SARMA.
Uso dei modelli ARMA
Se i parametri di un processo ARMA sono noti, il modello può essere usato per due scopi:
o previsione dell'andamento futuro della serie
e/o
o analisi delle sue (della serie) caratteristiche dinamiche.
Previsione
La
miglior previsione per i valori futuri di yt
si può calcolare sulla base di questo ragionamento: definiamo come previsore di
yt
una qualche funzione delle variabili contenute nel set informativo xT . Un previsore, cioè, è una qualche regola che
determina la previsione che facciamo su yt
dati i suoi valori precedenti, che
supponiamo di conoscere. Chiamiamo questo valore
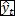 = f
(yt- ,
yt- ,
.). Naturalmente, questa regola ce la
inventiamo noi, e si pone il problema di inventarcela in modo che funzioni
"bene".
= f
(yt- ,
yt- ,
.). Naturalmente, questa regola ce la
inventiamo noi, e si pone il problema di inventarcela in modo che funzioni
"bene".
Se yt è un processo ARMA (o rappresentabile come tale), una volta che abbiamo il modello nella forma A(L)yt = C(L)єt , un'ipotesi sulla distribuzione di єt ci mette in condizione, almeno in linea di principio, di determinare la distribuzione della variabile casuale yt xT
È evidente che questo ci mette in grado anche di determinare la distribuzione condizionale dell'errore di previsione, cioè della variabile
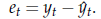
La distribuzione di et xT diventa rilevante se dobbiamo scegliere quale funzione usare come previsore. A rigore, una scelta ottimale dovrebbe essere fatta secondo questo criterio:
in primo luogo, scegliamo una funzione c(et) (cosiddetta di "perdita"), che associa un costo all'errore di previsione;
definiamo a questo punto la perdita "attesa" come
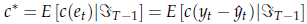
siccome c* è una funzione di
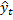 ,
scegliamo
,
scegliamo
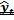 in modo tale da minimizzare c*, ossia "definiamo"
in modo tale da minimizzare c*, ossia "definiamo"
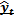 come quella funzione che minimizza il costo "atteso"
dell'errore di previsione.
come quella funzione che minimizza il costo "atteso"
dell'errore di previsione.
Dovrebbe essere chiaro a questo punto che quale sia il miglior previsore dipende dalle caratteristiche della "funzione di perdita" e per ogni problema pratico il previsore ottimo può essere diverso.
Per
fortuna, però, la faccenda diventa molto meno intricata se la funzione di
perdita è QUADRATICA, cioè se C(et
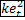 per k
positivo qualunque. In questo caso (che spesso può essere preso come
approssimazione soddisfacente della funzione di costo più appropriata) si può
dimostrare che
per k
positivo qualunque. In questo caso (che spesso può essere preso come
approssimazione soddisfacente della funzione di costo più appropriata) si può
dimostrare che
 coincide con il valore atteso condizionale:
coincide con il valore atteso condizionale:
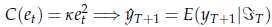
Questa proprietà è così comoda che nella stragrande maggioranza dei casi media condizionale come previsore senza neanche giustificare la scelta.
Dato un insieme di osservazioni che vanno da 1 a T, ammettiamo perciò che il miglior previsore di yT sia la sua media condizionale al set informativo di cui disponiamo, ossia
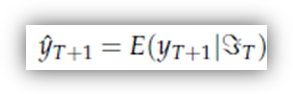
Nel caso di un modello AR puro, la soluzione è banale, poiché tutti i valori di y fino al tempo T sono noti, e quindi
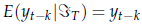
per qualunque k ≥ 0:
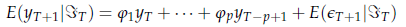
ma il valore di
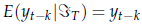
è evidentemente 0, poiché l'assenza di memoria del white noise garantisce che non ci sia informazione disponibile al presente sul futuro di є ; di conseguenza:
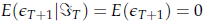
La previsione di yT+1 è quindi
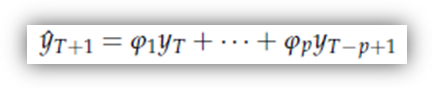
Visto
che ancora stiamo sul teorico, qui stiamo assumendo che il set informativo a
nostra disposizione si estenda infinitamente all'indietro nel passato, cosa che
ci semplifica molto le cose, perché significa che
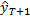 è facilmente calcolabile tramite l'equazione
di cui subito sopra. Se il nostro set informativo (come accade nella realtà) si
interrompe ad una qualche data iniziale, il meccanismo vale ancora per processi
solo "stazionari", anche se in modo più approssimato.
è facilmente calcolabile tramite l'equazione
di cui subito sopra. Se il nostro set informativo (come accade nella realtà) si
interrompe ad una qualche data iniziale, il meccanismo vale ancora per processi
solo "stazionari", anche se in modo più approssimato.
Naturalmente, la valutazione della media condizionale dà un valore puntuale, ma non dice nulla sull'attendibilità della previsione, cioè sulla dispersione dell'errore che ci attendiamo di commettere.
In termini più statistici, è necessario valutare anche la varianza dell'errore di previsione.
Nel caso più generale di processi ARMA, le previsioni si possono fare applicando ancora lo stesso concetto. In particolare, si noti che, se xt non ha limite temporale inferiore, allora esso comprende non solo tutti i valori passati di yt, ma anche quelli di єt, e quindi sono noti (nel senso "ricavabili da xt ") anche tutti i valori del white noise fino al tempo t-1.
A questo punto, si può applicare ad ogni ingrediente di un modello ARMA l'operatore valore atteso condizionale.
Esemplifico nel caso di un ARMA(1,1), perché una volta capito il concetto la generalizzazione è banale. Supponiamo quindi di sapere che il processo ha la forma
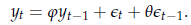
Mettiamoci all'istante 0, in cui non abbiamo alcuna osservazione. Qual è la migliore previsione che possiamo fare su y ? Visto che non abbiamo dati, la media condizionale coincide con la media marginale, e quindi
 = E(y
= E(y
Passa un periodo, e osserviamo il dato effettivo y . A questo punto, possiamo calcolare l'errore di previsione per il periodo 1, ossia
e = y
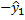 ;
poiché
;
poiché
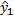 è 0,
per i motivi che abbiamo appena detto, ne consegue che e =
y .
A questo punto, possiamo calcolare
è 0,
per i motivi che abbiamo appena detto, ne consegue che e =
y .
A questo punto, possiamo calcolare
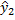 ,
con la seguente formula:
,
con la seguente formula:
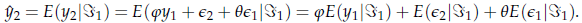
Ragioniamo un addendo per volta, tenendo a mente che x = y : evidentemente, i primi due termini non pongono problemi, perché
E(y x ) = y (è ovvio) e E(є x ) = 0 (per ipotesi). Ma che dire di E(є x )? Poiché є è anche interpretabile come l'errore di previsione che si commetterebbe al tempo 0 se il set informativo fosse infinito, allora la miglior previsione possibile che possiamo fare sull'errore di previsione al tempo 1 è esattamente l'errore di previsione che abbiamo effettivamente commesso: E(є x ) = e
In base a questo ragionamento, possiamo formulare la nostra previsione su y come
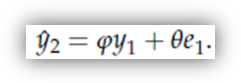
Facciamo
passare un altro periodo, e osserviamo y ;
da qui calcoliamo e ,
e il giochino prosegue, nel senso che a questo punto abbiamo tutto quel che ci
serve per calcolare
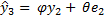 , eccetera eccetera.
, eccetera eccetera.
In pratica, le previsioni un passo in avanti su processi del tipo
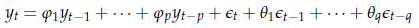
si fanno così:
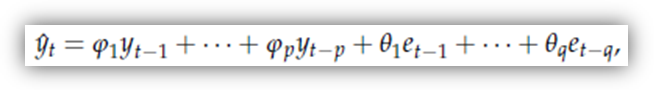
ovvero utilizzando i valori effettivamente osservati delle yt e i valori degli errori di previsione passati (et) al posto delle єt-
Analisi delle caratteristiche dinamiche (della serie)
Questo aspetto è generalmente indagato facendo uso della cosiddetta funzione di risposta. Cos'è la funzione di risposta di impulso? La risposta a questa domanda passa attraverso una considerazione che possiamo fare alla luce di quanto detto precedentemente. Consideriamo l'equazione
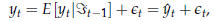
Il
valore di yt
può quindi essere interpretato come la somma di due componenti: una (
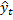 )
che, almeno in linea di principio, è perfettamente prevedibile dato il passato;
l'altra (єt)
assolutamente imprevedibile. In altri termini, si può pensare che il valore di yt
dipenda da una componente di persistenza a cui si somma un disturbo, o, come si
usa dire, shock casuale che riassume
tutto ciò che è successo al tempo t
che non poteva essere previsto. L'effetto di questa componente (єt),
tuttavia, si riverbera anche nel futuro della serie yt
attraverso l'effetto persistenza. È per questo che, sovente, il white noise єt
viene chiamato, in forma più neutra, errore di previsione ad un passo.
)
che, almeno in linea di principio, è perfettamente prevedibile dato il passato;
l'altra (єt)
assolutamente imprevedibile. In altri termini, si può pensare che il valore di yt
dipenda da una componente di persistenza a cui si somma un disturbo, o, come si
usa dire, shock casuale che riassume
tutto ciò che è successo al tempo t
che non poteva essere previsto. L'effetto di questa componente (єt),
tuttavia, si riverbera anche nel futuro della serie yt
attraverso l'effetto persistenza. È per questo che, sovente, il white noise єt
viene chiamato, in forma più neutra, errore di previsione ad un passo.
L'idea, a questo punto, è la seguente: se scriviamo il processo in forma MA
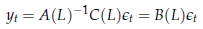
si può pensare all'i-esimo coefficiente del polinomio B(L) come all'effetto che lo shock avvenuto i periodi addietro ha sul valore attuale di y, o, equivalentemente, all'impatto che gli avvenimenti di oggi avranno sulla serie studiata fra i periodi.
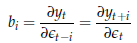
La funzione di risposta di impulso, insomma, è data semplicemente dai coefficienti della rappresentazione MA del processo, e viene generalmente esaminata con un grafico che ha in ascissa i valori di i ed in ordinata i valori di bi
Per calcolarsi la rappresentazione di Wold di un processo ARMA di cui siano noti i parametri, quindi, bisogna calcolarsi il polinomio inverso di A(L). Questo può essere piuttosto noioso, specie se l'ordine della parte auto regressiva è alto. Un algoritmo di calcolo decisamente più semplice, che può essere implementato anche su un comune foglio elettronico, è il seguente:
definite una serie et che contiene tutti zeri fuorché per un periodo, in cui vale 1 (detto in un altro modo, definite una et per cui e = 1, e
et = 0 per t ≠ 0);
definite una serie it, che imponete uguale a 0 per t < 0; per t ≥ 0, invece, valga A(L) it = C(L) et
I valori che otterrete per la serie it sono esattamente i valori della funzione di risposta di impulso.
Stima dei modelli ARMA
Fino ad ora abbiamo fatto finta che il processo stocastico che sovrapponiamo ai dati per interpretarli fosse governato da PARAMETRI "noti". Se questi ultimi NOTI NON sono (e non lo sono mai), si possono utilizzare delle loro STIME. La tecnica di base per la stima dei parametri di un processo ARMA è la MASSIMA VEROSIMIGLIANZA. Di solito si assume che il processo sia normale, cosicché la forma della funzione di densità delle osservazioni è nota e trattabile.
Può essere utile richiamare brevemente cosa si intende per funzione di verosimiglianza. La verosimiglianza è la funzione di densità del campione, calcolata nel punto corrispondente al campione osservato. Essa dipenderà da un vettore ψ di parametri "incogniti", che ne determinano la forma. Per questo la scriviamo L(ψ). "Massimizzando" questa funzione rispetto a ψ si ottiene la stima di massima verosimiglianza.
Quando osserviamo una realizzazione di un processo stocastico (o, per meglio dire, una serie storica che possiamo pensare come tale) x , . , xT, la funzione di verosimiglianza non è altro che la funzione di densità congiunta della parte di processo osservata, ossia la funzione di densità marginale del vettore aleatorio (x , . , xT), calcolata nei valori osservati; nel caso di un processo ARMA del tipo
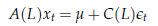
essa dipenderà dal vettore di parametri ψ = .
Se supponiamo (come generalmente si fa) che il processo sia gaussiano, la funzione di verosimiglianza non è che la funzione di densità di una normale multivariata:
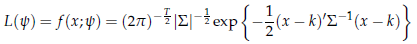
dove x è il vettore (x , . , xT) delle T osservazioni; k e ∑ sono i suoi momenti primi e secondi, che dipendono da ψ. Ad esempio, l'elemento ij della matrice ∑ non è che l'autocovarianza di ordine │i-j│ la quale, come sappiamo, è una funzione dei parametri del processo ARMA.
È possibile dimostrare che gli stimatori di massima verosimiglianza di processi ARMA gaussiani sono consistenti, asintoticamente normali ed asintoticamente efficienti. Inoltre, sotto condizioni piuttosto blande, le proprietà di consistenza e normalità asintotica vengono conservate anche quando la vera distribuzione del processo non sia normale (si parla in questo caso di stime di quasi-massima verosimiglianza).
Da un punto di vista teorico, è detto tutto. Da un punto di vista pratico, i problemi sono appena all'inizio. Innanzitutto, va detto che come al solito non si lavora sulla funzione L(ψ), ma sul suo logaritmo
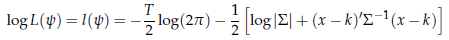
ma questo è irrilevante. I problemi principali sono tre:
in primo luogo, il
sistema di equazioni che risulta uguagliando a 0 il vettore dello score s(ψ) =
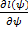 è non lineare, ed in generale non si riesce a
risolvere analiticamente, per cui non sono disponibili espressioni che
permettano di calcolare gli elementi di
è non lineare, ed in generale non si riesce a
risolvere analiticamente, per cui non sono disponibili espressioni che
permettano di calcolare gli elementi di
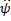 come semplici funzioni dai dati;
come semplici funzioni dai dati;
non è noto l'ordine dei polinomi A(L) e C(L) adatti a rappresentare in modo adeguato il processo di cui pensiamo xt sia una realizzazione;
per calcolare L(ψ) bisogna conoscere la matrice ∑; ora, la matrice ∑ è una matrice TxT, e quando T è grande (già nell'ordine delle decine, ma i campioni di serie storiche possono assumere dimensioni dell'ordine di decine di migliaia di osservazioni) anche il semplice calcolo dei suoi elementi in funzione di ψ è un problema non da poco, per non parlare del suo determinante o della sua inversa.
I MODELLI ARIMA
I modelli ARIMA (autoregressivi INTEGRATI a media mobile ) di Box e Jenkins partono dal presupposto che fra due osservazioni di una serie quello che altera il livello della serie è il cosiddetto disturbo.
Un modello generale di Box-Jenkins viene indicato come ARIMA (p,d,q) dove:
![]() AR=AutoRegression
(autoregressione) e p è l'ordine
della stessa,
AR=AutoRegression
(autoregressione) e p è l'ordine
della stessa,
![]() I=Integration (integrazione)
e d è l'ordine della stessa,
I=Integration (integrazione)
e d è l'ordine della stessa,
![]() MA=Moving Average
(media mobile) e q è l'ordine delle
stessa.
MA=Moving Average
(media mobile) e q è l'ordine delle
stessa.
Pertanto un modello ARIMA (p,d,q) è analogo ad un modello ARMA(p,q) applicato alle differenze d'ordine 'd' della serie dei valori, invece che agli effettivi valori.
Se la serie non è "stazionaria" (la media e la varianza non sono costanti nel tempo) essa viene integrata a livello 1 o 2, dopo aver eseguito un'eventuale trasformazione dei dati (solitamente quella logaritmica). In tal modo viene ottenuta una serie "stazionaria" (random walk).
) da
questo discende che esistono anche tutti i momenti secondi incrociati E(
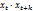 ), con k qualunque, e anch'essi non dipendono
da t (anche se possono dipendere da k).
), con k qualunque, e anch'essi non dipendono
da t (anche se possono dipendere da k).
) Il venire meno di una di queste ipotesi potrebbe inficiare la validità del modello adottato e far propendere per altri modelli più complessi oppure di intervenire sulla serie con delle trasformazioni atte, ad esempio, a stabilizzare la varianza oppure ad eliminare l'autocorrelazione. Tali test risultano necessari anche nell'ambito dell'approccio stocastico delle serie storiche.
 |
|
| Appunti Geografia |  |
| Tesine Fisica |  |
| Lezioni Contabilita |  |