 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2236 | Gradito: |
Leggi anche appunti:La legge di hardy - weinbergLA LEGGE DI HARDY - WEINBERG Nel 1908 G. H. Hardy e W. Weinberg definirono Il teorema degli incrementi finiti(o di Cauchy)Il teorema degli incrementi finiti(o di Cauchy) Se F(x) e φ(x) ProspettiveProspettive La rappresentazione prospettica vera e propria, se trova largo |
 |
 |
MATEMATICA. . . MENTE
Come riporta la risoluzione approvata dalla Conferenza generale dell'Unesco del 2000, dichiarato 'Anno mondiale della matematica',
![]() la matematica e le sue applicazioni hanno importanza centrale
nel mondo d'oggi per la scienza, la tecnologia, le comunicazioni, l'economia e
numerosi altri campi
la matematica e le sue applicazioni hanno importanza centrale
nel mondo d'oggi per la scienza, la tecnologia, le comunicazioni, l'economia e
numerosi altri campi
![]() la matematica ha profonde radici in molte culture e i più
eminenti pensatori, per migliaia d'anni, hanno contribuito in maniera
significativa al suo sviluppo
la matematica ha profonde radici in molte culture e i più
eminenti pensatori, per migliaia d'anni, hanno contribuito in maniera
significativa al suo sviluppo
![]() il linguaggio e i valori della matematica sono universali e
la rendono perfettamente adatta alla cooperazione internazionale
il linguaggio e i valori della matematica sono universali e
la rendono perfettamente adatta alla cooperazione internazionale
![]() l'educazione matematica ha un ruolo chiave nella scuola
primaria e secondaria, sia per la comprensione di concetti matematici di base,
sia per lo sviluppo del pensiero razionale
l'educazione matematica ha un ruolo chiave nella scuola
primaria e secondaria, sia per la comprensione di concetti matematici di base,
sia per lo sviluppo del pensiero razionale
È quindi riconosciuta a livello mondiale l'importanza fondamentale di questa disciplina, probabilmente una fra le più antiche, dato che la necessità di contare si è sviluppata fin dalla trasformazione dell'uomo da cacciatore ad agricoltore o allevatore, e ne è una testimonianza il primo conteggio scritto (tacche raggruppate cinque a cinque) ritrovato su un osso di lupo risalente a quasi 30000 anni fa.
La scelta della presenza e della moltitudine delle interazioni e dei collegamenti fra la matematica e le altre discipline come argomento della tesina, nasce però dal riscontro che tali collegamenti spesso non vengono evidenziati, tanto da affermare una totale separazione dell'ambito scientifico da quello umanistico.
Al contrario, questa vuole essere una tesi sperimentale che dimostri il contrario, e che affermi l'importanza e la necessità di porre maggiore attenzione al collegamento fra la matematica e le altre discipline, come mezzo per arrivare a una formazione in cui non si debba distinguere tra cultura classica e scientifica, entrambe necessarie e fondamentali.
Nella società contemporanea sono troppi e annosi i dibattiti che mettono ad esempio in discussione il rapporto fra fede e scienza, questione questa aperta da sempre, ma sarebbe necessario invece allargare gli orizzonti verso una nuova cultura che possa accogliere indistintamente ogni disciplina, anche e soprattutto per abituare le coscienze comuni ad una apertura che potrebbe poi estendersi ad ogni ambito, anche a quello sociale.
In secondo luogo questa tesina vuole essere una sorta di sfida per dimostrare che in fondo, quella matematica odiata dalla maggior parte degli studenti, che concordano con Venditti, che la notte prima degli esami affermava 'la matematica non sarà mai il mio mestiere', è in fondo in tutto ciò che ci circonda, e non si può affatto prescindere da essa per comprendere a fondo la realtà e le leggi che la regolano.
Nonostante il pensiero comune, che la matematica serve in effetti solo a far di conto, questa materia si potrebbe definire arte, l'arte del ragionare, del riflettere, dello sviluppare un senso critico, che in effetti rappresentano i reali obiettivi dell'insegnamento scolastico.
 All'improvviso gli parve di essere ritornato ad
Harvard, davanti ai suoi studenti del corso 'il simbolismo nell'arte'
e di scrivere alla lavagna il suo numero preferito.
All'improvviso gli parve di essere ritornato ad
Harvard, davanti ai suoi studenti del corso 'il simbolismo nell'arte'
e di scrivere alla lavagna il suo numero preferito.
1,618
Langdon si era voltato verso la sua aula piena di studenti ansiosi. 'Chi mi sa dire che numero è?'
Un diplomato in matematica, nelle ultime file, aveva alzato la mano. 'Il numero phi '. Lo pronunciava 'fi'.
'Bene, Stettner' aveva commentato Langdon. 'Signori, vi presento phi'. 'Da non confondere con il pi greco' aveva commentato Stettner, sorridendo 'come diciamo noi matematici, il phi è di un'acca più interessante del pi.'
Langdon aveva riso, ma nessun altro aveva capito la battuta. Stettner era tornato a sedere deluso.
'Questo numero phi' aveva continuato Langdon, 'uno virgola seicento diciotto, è un numero molto importante per l'arte. chi mi sa dire il perché?'
Stettner aveva cercato di riabilitarsi. 'Perchè è bello?'. Tutti avevano riso.
'A dire il vero', aveva commentato Langdon , ' Stettner ha di nuovo ragione. In genere, phi è considerato il più bel numero dell'universo.'
Le risate erano cessate e subito Stettner aveva sorriso.
Mentre caricava il proiettore delle diapositive, Langdon aveva spiegato che il numero 'phi' veniva dalla sequenza di Fibonacci, una progressione famosa non solo perché la somma di due termini adiacenti era uguale al termine successivo, ma perché il quoziente di due numeri adiacenti tendeva sorprendentemente al valore 1, 618, phi!
Nonostante la bizzarra origine matematica del phi, aveva spiegato Langdon, il suo più sorprendente aspetto era il suo ruolo di mattone fondamentale della natura. Piante, animali e persino uomini avevano misure che rispettavano esattamente il rapporto tra phi e uno.
'L'onnipresenza del phi in natura' aveva detto Langdon mentre spegneva la luce, 'va chiaramente al di là delle coincidenze e perciò gli antichi pensavano che fosse stato stabilito dal Creatore dell'universo. I primi scienziati la chiamarono ' proporzione divina'.
' Un momento,' aveva detto una giovane donna seduta in prima fila. 'Io sono diplomata in biologia e non ho mai visto questa divina proporzione in natura.'
' No?' Langdon aveva sorriso. 'Non ha mai studiato il rapporto tra femmine e maschi in un alveare?'
'Certo, le femmine sono sempre in numero superiore ai maschi.'
' Esatto. E sa che se in qualsiasi alveare si prende il numero delle femmine e lo si divide per quello dei maschi si ottiene sempre lo stesso numero?'
'Davvero?'
' Si, Il numero phi.'
La ragazza era rimasta a bocca aperta. ' non è possibile!', ' certo che lo è!' aveva ribattuto Langdon, sorridendo, e aveva proiettato la diapositiva di una conchiglia. 'riconosce questa?' ' E' un nautilus', aveva detto la diplomata in biologia ' un mollusco cefalopode che pompa gas nelle camere della sua conchiglia per regolare la spinta di galleggiamento.' , ' Esatto: E mi sa dire il rapporto tra il diametro di una spira e quello della successiva?'
La ragazza aveva guardato con aria incerta le curve concentriche della spirale del nautilus. Langdon aveva annuito. ' phi, la proporzione divina, uno virgola seicentodiciotto a uno.'
La ragazza l'aveva guardato con aria stupita.
Langdon era passato alla successiva diapositiva, l'ingrandimento dei semi di un girasole. ' i semi di girasole crescono secondo spirali opposte. chi sa dire il rapporto tra una rotazione e la successiva?'
' il numero phi?' avevano chiesto tutti.
'Tombola!'
Langdon aveva continuato a proiettare altre diapositive, ma assai più in fretta: una pigna e la sua suddivisione secondo due serie di spirali, la disposizione delle foglie sui rami, i segmenti di alcuni insetti. Tutti rispettavano in modo stupefacente la proporzione divina.
'Incredibile' aveva esclamato qualcuno. ' d'accordo,' - aveva commentato qualcun altro 'ma cosa c'entra con l'arte?'
'Ah!' aveva esclamato Langdon, ' sono lieto che l'abbia chiesto.' Proiettò un'altra diapositiva: una pergamena ingiallita in cui si scorgeva il famoso nudo maschile di Leonardo da Vinci, l'uomo vitruviano, così chiamato dal nome di Marco Vitruvio, il grande architetto romano che aveva tessuto le lodi della proporzione divina nel suo libro De Architectura.
' Nessuno capiva meglio di Leonardo da Vinci la divina struttura del corpo umano. Leonardo disseppelliva i corpi per misurare le proporzioni esatte della struttura ossea umana. Fu il primo a mostrare che il corpo umano è letteralmente costituito di elementi che stanno tra di loro in rapporto di phi.'
Tutti l'avevano guardato con aria dubbiosa. 'Non mi credete?' li aveva sfidati Langdon, ' la prossima volta che fate la doccia, portatevi un metro.'
Un paio di giocatori di football avevano riso di lui. ' Non soltanto voi scimmioni insicuri' aveva continuato Langdon. 'Tutti, maschi e femmine. Fate la prova. Misurate la vostra altezza poi dividetela per la distanza da terra del vostro ombelico. Indovinate che numero si ottiene.'
'Non phi!' aveva detto uno degli 'scimmioni'. 'Proprio phi, invece' - aveva risposto Langdon. ' uno virgola seicentodiciotto. Volete un altro esempio? Misurate la distanza dalla spalla alla punta delle dita e dividetela per la distanza dal gomito alla punta delle dita. Di nuovo phi. Altro esempio? Dal fianco al pavimento diviso per la distanza dal ginocchio al pavimento. di nuovo phi. Le articolazioni delle dita, le sezioni della colonna vertebrale, Ancora phi. Amici miei ciascuno di voi è il tributo ambulante alla proporzione divina.'
 Quello
della sezione aura è un argomento che ha affascinato e affascina chiunque si
appresti a capirne gli infiniti ambiti in cui la si ritrova ed il mistero che
la avvolge proprio per questo motivo.
Quello
della sezione aura è un argomento che ha affascinato e affascina chiunque si
appresti a capirne gli infiniti ambiti in cui la si ritrova ed il mistero che
la avvolge proprio per questo motivo.
Studiata per la prima volta dai pitagorici, è stata inizialmente definita come il rapporto fra la diagonale e il lato di un pentagono regolare, le cui diagonali formano una stella a cinque punte, usata inizialmente dagli stessi Pitagorici (che la chiamavano pentagramma), e poi fino alle Brigate Rosse, passando per la tradizione ebraica, che la considerava «sigillo di Salomone», per la letteratura di Goethe, come «piede di strega» che impedisce a Mefistofele di uscire dallo studio di Faust, e per la bandiera americana, che la contiene insieme alle strisce.
A parte il simbolo, la sezione aurea corrisponde ad un numero, (radice di5 - 1)/2, uguale a circa 1,618, che rappresenta una proporzione e che ricorre incredibilmente in molteplici aspetti della realtà, fu usata ad esempio nella costruzione della Grande Piramide e del Partenone, la si ritrova nel corpo umano, fra le lunghezze di falangi consecutive delle dita di una mano e non solo, o in natura, nella spirale delle conchiglie Nautilus.

Successivamente ai pitagorici,
molti si sono interessanti di questo numero misterioso, soprattutto durante il
Rinascimento, ma il libro più famoso sull'argomento è probabilmente il De
divina proportione, che Luca Pacioli, nel 1509, scrisse in collaborazione  addirittura con Leonardo da
Vinci, il quale dedicò inoltre molti suoi studi a tale argomento, con una serie
di tavole che rappresentano le proporzioni esistenti fra gli elementi del corpo
umano. Secondo lo stesso Pacioli ed Albrecht Durer, la sezione aurea era
elemento proporzionale analogico tra la figura umana e la natura
oggettiva. La presenza del numero d'oro ricorre quindi in architettura,
pittura, fisica, matematica, botanica, e tale fenomeno è inspiegabile, anche
se, per quanto riguarda le arti, alcuni esperimenti hanno dimostrato che la
percezione umana mostra una naturale preferenza per le proporzioni in accordo
con la sezione aurea, e che quindi gli artisti tenderebbero quasi
inconsciamente a disporre gli elementi di una composizione in base a tali
rapporti.
addirittura con Leonardo da
Vinci, il quale dedicò inoltre molti suoi studi a tale argomento, con una serie
di tavole che rappresentano le proporzioni esistenti fra gli elementi del corpo
umano. Secondo lo stesso Pacioli ed Albrecht Durer, la sezione aurea era
elemento proporzionale analogico tra la figura umana e la natura
oggettiva. La presenza del numero d'oro ricorre quindi in architettura,
pittura, fisica, matematica, botanica, e tale fenomeno è inspiegabile, anche
se, per quanto riguarda le arti, alcuni esperimenti hanno dimostrato che la
percezione umana mostra una naturale preferenza per le proporzioni in accordo
con la sezione aurea, e che quindi gli artisti tenderebbero quasi
inconsciamente a disporre gli elementi di una composizione in base a tali
rapporti.
Per quanto riguarda la matematica, ad esempio, è particolarissima la questione della sequenza di Fibonacci, successione di numeri in cui ogni termine è uguale alla somma dei due numeri precedenti e in cui il rapporto tra due termini successivi si avvicina incredibilmente a un numero.phi, la sezione aurea!
E in arte e architettura? I Greci furono i primi a sfruttare la proporzione fra 1 e phi: in un'anfora greca, e si parla almeno del III secolo a.C., il diametro maggiore sta al diametro del collo come 1:0,618, il listello all'altezza dei manici divide l'altezza totale in una proporzione aurea, e esiste tale rapporto anche tra la fascia decorata a figure e la parte superiore del vaso. La sezione aurea è stata poi applicata nella costruzione di templi: il rapporto tra lunghezza e larghezza era 1:0,618!
Anche in pittura phi ha trovato il suo spazio.in alcuni quadri de Rinascimento ricorre moltissime volte, ad esempio nella raffigurazione di un panorama l'orizzonte deve dividere l'altezza del quadro secondo la sezione aurea per ottenere un risultato più soddisfacente (e ritroviamo tale rapporto anche nella pittura dell'800, in 'Domenica pomeriggio alla grande Jatte' di Seurat).
UMANISTICO & SCIENTIFICO:
DUE MONDI A SE'?
E' stata spesso messa in discussione la possibilità di eventuali legami fra campo umanistico e scientifico, ambiti che, soprattutto in passato, sono stati ritenuti inconciliabili da gran parte degli intellettuali.
In realtà i legami esistono e sono moltissimi, e non solo fra gli autori contemporanei, dell'era della miscellanea, ma anche in scrittori e letterati di epoche passate, primo fra tutti il padre della letteratura italiana, Dante Alighieri.
Approfondendo la ricerca, si scopre ad esempio che molti scrittori di fama e valore risaputo, erano matematici, e viceversa che si attribuiscono a molti scienziati pubblicazioni di notevole valore letterario.
Al primo caso appartengono ad esempio l'autore di Dracula, Bram Stocker, e Lewis Carroll, (il cui Alice nel paese delle meraviglie è uno dei classici della letteratura per bambini), pseudonimo di Charles Dodgson, professore a cui si attribuiscono numerosi trattati di geometria.
E' inoltre ricorrente
ritrovare accenni di matematica e fisica nelle opere di grandi autori, e a
parte i casi emblematici delle opere di Dante(il Convivio e
E ancora ritroviamo riferimenti in Edgar Allan Poe, in Kafka, Calvino e Buzzati.
Esempi poi tipici di come, soprattutto nella letteratura più recente si è cercato di muoversi sempre più in direzione della matematica, sono Flatland di Edwin Abbott, che descrive dettagliatamente la geometria di un mondo piatto piano (il cosiddetto «planiverso»), Sphereland di Dionys Burger, che descrive un mondo piatto ma sferico, I racconti scientifici di Charles Hinton, che sperimentano invece un mondo quadridimensionale e Centomila miliardi di poemi di Raymond Queneau, basati sul calcolo combinatorio.
Tantissimi sono poi i riferimenti numerologici in Dante, riguardanti molteplici branche della matematica, dalla geometria
O cara piota mia, che sì t'insusi,
che come veggion le terreni menti
non capere in triangol due ottusi.
Paradiso, XVII 13 - 15:
(che si riferisce al fatto che in un triangolo non possono esserci due angoli ottusi)
Qual è 'l geomètra che tutto s'affigge
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige,
tal era io a quella vista nova;
veder volea come si convenne
l'imago al cerchio e come vi s'indova
(il chiaro riferimento è qui all'annosa questione della quadratura del cerchio)
alla probabilità,
Quando si parte il gioco della zara,
colui che perde sì riman dolente
repetendo le volte, e tristo impara.
Purgatorio, VI, 1-3
Interessante è poi la questione del XXXIIIsimo Canto del Purgatorio, nel quale la frase 'nel quale un cinquecento diece e cinque' ha fatto discutere.
Scrivendo infatti il numero con la notazione romana, si ottiene DXV, ritenuto da molti un anagramma. Potrebbe infatti riferirsi a DUX, Arrigo VII, al monogramma greco di Cristo, o ancora a Domini Xristi Vergatus, la misteriosa figura del Veltro che ha lasciato molti dibattiti aperti, o a Domini Xristi Vicarius, il Papa.
Facendo invece
riferimento alla notazione araba, anche se non si ha la sicurezza che Dante la
conoscesse già, il DXV potrebbe diventare 515, che i numerologi indicano come
distanza tra Terra e Cielo, espressa in anni, facendo riferimento ad Ezechiele,
o ancora, considerando la lingua greca,
Ma esaminiamo degli esempi più concreti.
L'incendio suo seguiva ogni scintilla;
ed eran tante, che 'l numero loro
più che 'l doppiar delli scacchi s'immilla.
 Ci troviamo nel XXVIII canto del Paradiso, in cui Dante
tratta la questione della funzione degli Spiriti Angelici e della loro
eventuale presenza, che è stata fulcro di molti dibattiti dei teologi
medioevali.
Ci troviamo nel XXVIII canto del Paradiso, in cui Dante
tratta la questione della funzione degli Spiriti Angelici e della loro
eventuale presenza, che è stata fulcro di molti dibattiti dei teologi
medioevali.
Gli ordini angelici appaiono come nove cerchi di fuoco concentrici che ruotano con una velocità che è proporzionalmente inversa alla loro distanza dal centro, punto luminoso che rappresenta Dio.
I versi si riferiscono in particolare al numero degli angeli, argomento affrontato anche in molti passi della Bibbia e dallo stesso Dante nel Convivio, numero che l'autore ritiene particolarmente significativo, tanto da utilizzare un paragone che lo mette a confronto con una cifra che, data la sua enormità, è quasi impensabile.
Dante si rifà alla leggenda di Sissa Nasir, inventore degli scacchi decapitato perché il sovrano a cui propose la sua invenzione si sentì preso in giro dalla ricompensa richiestagli, che apparentemente sembrava invece essere molto modesta.
Il furbo Nasir, mostrandogli la scacchiera 8 X 8 gli richiese infatti un chicco di grano per la prima casella, due per la seconda, quattro per la terza, otto per la quarta e così via fino alla 64esima, l'ultima.
Per comprendere meglio l'entità della cifra che ne sarebbe derivata si ricorre spesso a un espediente, immaginare cioè di distribuire i chicchi di Nasir sulla superficie terrestre, che oggi sappiamo pari a 5,0995X10alla18 cm2: dato che i chicchi risulterebbero 18 446 744 073 709 551 615 otterremmo 3 chicchi e mezzo per ogni cm2 della superficie terrestre; il numero a cui Dante accenna è però ancora più grande, perché 'più che raddoppiare di casella in casella', 's'inmilla', e con lo stesso calcolo fatto precedentemente avremmo un numero immenso, 10 alla 189, di angeli per ogni cm2!
Ma come si ottiene un numero così elevato?
PROGRESSIONI GEOMETRICHE
Una progressione geometrica è una successione di numeri tali che il quoziente tra due elementi consecutivi è sempre uguale a un numero costante, detto ragione della successione.
Un esempio può essere il seguente:
Il quoziente costante, che nell'esempio è 2, si chiama ragione della progressione geometrica e si indica con q.
Il termine n-esimo di una progressione può quindi essere definito così:
an = an-1 · q
Il termine n-esimo di una progressione geometrica, noto il primo termine e la ragione è:
an= a · q^(n-1)
Quindi in una progressione geometrica:
![]() se q > 0 i termini sono tutti
o positivi o negativi
se q > 0 i termini sono tutti
o positivi o negativi
![]() se q < 0 i termini sono alternativamente
positivi e negativi.
se q < 0 i termini sono alternativamente
positivi e negativi.
Il termine di posto s di una progressione geometrica, noto il termine di posto r e la ragione è:
as= ar · q^(s-r)
Il prodotto di due termini equidistanti dagli estremi di una progressione geometrica è costante ed è uguale al prodotto dei termini estremi.
La somma dei primi n termini di una progressione geometrica di ragione q è:
Sn =a (q^n
q-1
Il prodotto dei primi n termini di una progressione geometrica di ragione q è uguale alla radice del prodotto del primo e dell'ultimo termine, elevata all'indice di quest'ultimo.
E ancora.
Come quando da l'acqua o da lo specchio
salta lo raggio a l'opposita parte,
saltando su per lo modo parecchio
a quel che scende, e tanto si
diparte
dal cader de la pietra in igual tratta,
sì come mostra esperienza e arte;
così mi parve da luce
rifratta
quivi dinanzi a me esser percosso;
per che a fuggir la mia vista fu ratta.
Come quando dall'acqua o da uno specchio un raggio rimbalza verso la parte opposta, risalendo allo stesso modo
di com'era disceso, e si allontana dalla perpendicolare per un tratto uguale, così come dimostrano l'esperienza e la scienza;
così mi sembrò di essere colpito da una luce riflessa proprio davanti a me; per cui la mia vista fu pronta a sfuggirne.
Purgatorio, XV
E
sì come secondo raggio suole
uscir dal primo e risalire in suso,
pur come pelegrin che tornar vuole,
così de l'atto suo, per li
occhi infuso
ne l'imagine mia, il mio si fece,
e fissi li occhi al sole oltre nostr'uso.
E come il raggio riflesso è determinato solitamente dal raggio incidente, e ritorna alla sorgente come un pellegrino che voglia tornare [come un falco pellegrino che risale dopo essere piombato sulla preda],
così da questo gesto di Beatrice, entrato nella mia facoltà immaginativa attraverso gli occhi, derivò il mio sguardo e fissai gli occhi nel Sole in modo non consentito alle capacità umane.
Paradiso, I
In entrambi questi passaggi, che appartengono rispettivamente al XV Canto del Purgatorio e al I del Paradiso, Dante accenna al fenomeno della riflessione, uno dei più caratteristici effetti della luce.
Nel primo, Dante procede verso Ovest scortato da Virgilio, finchè una luce abbagliante lo investe, impedendogli la vista e costringendolo a voltarsi: la luce proviene dall'angelo della mansuetudine, che li accoglie per condurli al girone superiore; nel secondo passo, Dante e Beatrice sono in volo verso il Cielo della Luna, e Dante è stupito dal fatto che gli è possibile fissare il Sole, cosa non normalmente consentita alle facoltà umane.
E' particolare, soprattutto nelle terzine del Purgatorio, l'attenzione particolare che Dante ha nel descrivere minuziosamente il fenomeno, e la più comune interpretazione attribuita a tale atteggiamento è il voler evidenziare l'estrema armonia della natura, che attraverso la particolarità delle sue leggi e dei suoi comportamenti ci mostra la presenza di Dio.
RIFLESSIONE E RIFRAZIONE
Francesco Maria Grimaldi,
De Lumine
La luce, emessa da sorgenti primarie, sole, lampadina, fiamma, si propaga attraverso mezzi trasparenti e anche attraverso il vuoto. I fenomeni quali riflessione, rifrazione etc si hanno quando le onde luminose incontrano un ostacolo, o più in generale una discontinuità, e la luce non viaggia così indisturbata dalla sorgente in poi.
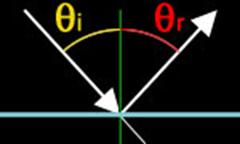 Nella riflessione speculare, che avviene quando la luce
incide su superfici lucide, ad ogni raggio incidente che colpisce la suddetta
superficie, corrisponde un solo raggio riflesso. Chiamando angolo di incidenza
Nella riflessione speculare, che avviene quando la luce
incide su superfici lucide, ad ogni raggio incidente che colpisce la suddetta
superficie, corrisponde un solo raggio riflesso. Chiamando angolo di incidenza ![]() l'angolo formato dal raggio e la normale alla
superficie e angolo di riflessione
l'angolo formato dal raggio e la normale alla
superficie e angolo di riflessione ![]() quello formato dalla normale e dal raggio
riflesso, si ottiene che l'angolo di riflessione è uguale all'angolo di
incidenza e che il raggio riflesso, quello incidente e la normale staranno
nello stesso piano.
quello formato dalla normale e dal raggio
riflesso, si ottiene che l'angolo di riflessione è uguale all'angolo di
incidenza e che il raggio riflesso, quello incidente e la normale staranno
nello stesso piano.
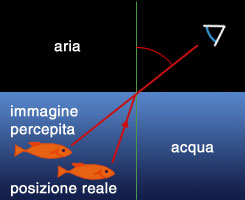 Quando un raggio luminoso passa da un materiale ad un altro
la radiazione cambia direzione di propagazione: questo fenomeno si chiama
rifrazione. L'entità della deviazione dipende dalla differenza di indice di
rifrazione tra i due materiali.
Quando un raggio luminoso passa da un materiale ad un altro
la radiazione cambia direzione di propagazione: questo fenomeno si chiama
rifrazione. L'entità della deviazione dipende dalla differenza di indice di
rifrazione tra i due materiali.
Proprio questa deviazione è la ragione per cui quando guardiamo in acqua
vediamo gli oggetti spostati rispetto alla loro posizione reale e le aste
sembrano spezzate. L'indice di rifrazione di un materiale dipende alla
lunghezza d'onda della radiazione, e questo provoca il fenomeno della dispersione.
.Non esiste cosa alcuna che l'arte non possa esprimere.
Oscar Wilde
Sono innegabili i rapporti che intercorrono fra matematica e arte, tanto che la stessa matematica è stata più volte definita essa stessa una forma d'arte, l'arte dei numeri.
Anche riferendosi alle arti figurative e all'architettura è inevitabile imbattersi in legami con la matematica, da cui l'architettura non può prescindere e che è presente spesso, anche se forse più velatamente, in molte opere pittoriche.
A iniziare dalla prospettiva, che è la rappresentazione realistica di scene spaziali su un piano, e che è stata ampiamente utilizzata da Brunelleschi e da Piero della Francesca, dopo la teorizzazione di Leon Battista Alberti, e continuando con Leonardo(di cui è celebre anche il motto "proibita la lettura ai non matematici", ripreso forse da Platone), il primo ad introdurre, attorno al 1500, le anamorfosi, rappresentazioni che appaiono corrette soltanto se osservate da un punto di vista particolare, che ispirarono la geometria proiettiva, lo studio delle proprietà che sono invarianti rispetto a proiezione(che si sviluppò in una delle branche fondamentali della matematica), la matematica ha quindi costituito da sempre un elemento importante per l'arte.
Ma oltre gli artisti più antichi, come Paolo Uccello, che venne addirittura «accusato» dal Vasari di essere più un matematico che un artista, o Albrecht Dürer, che scrisse un libro sulle figure piane e solide, e produsse l'incisione Melanconia, in cui compaiono strani solidi ed un quadrato magico, notiamo affinità con la matematica anche analizzando le avanguardie del '900.
 Wassily Kandinsky, che fondò con Franz Marc la corrente Der
blaue reiter, ("Il cavaliere azzurro"), può aiutarci a capire meglio il valore
ed il significato della matematica nell'arte, in quanto teorizzò nell'opera 'Lo
spirituale nell'arte', la sostituzione dell'immaginazione dell'artista con la
concezione matematica, e sviluppò questo tema pochi anni dopo in Punto, linea e
superficie.
Wassily Kandinsky, che fondò con Franz Marc la corrente Der
blaue reiter, ("Il cavaliere azzurro"), può aiutarci a capire meglio il valore
ed il significato della matematica nell'arte, in quanto teorizzò nell'opera 'Lo
spirituale nell'arte', la sostituzione dell'immaginazione dell'artista con la
concezione matematica, e sviluppò questo tema pochi anni dopo in Punto, linea e
superficie.
Kandinsky, che afferma che "in ultima analisi ogni forza trova espressione nel numero', e che "un giorno o l'altro ogni composizione potrà ricevere un'espressione numerica', teorizzò insomma una nuova scienza dell'arte, basata su regole scientifiche e matematiche, da porre alla base della pittura, simili a quelle che ci sono nell'architettura e nella musica.
 Oltre Kandinsky, anche Mondrian e Dalì ebbero rapporti con la
matematica, il primo infatti paragonava il suo Neoplasticismo, (piani
rettangolari colorati), all'astrattismo della matematica, mentre Dalí ambientò
l'Ultima cena in una struttura dodecaedrica simboleggiante i 12 apostoli,
rappresentò nella Crocifissione la croce come sviluppo tridimensionale di un
ipercubo, e strutturò
Oltre Kandinsky, anche Mondrian e Dalì ebbero rapporti con la
matematica, il primo infatti paragonava il suo Neoplasticismo, (piani
rettangolari colorati), all'astrattismo della matematica, mentre Dalí ambientò
l'Ultima cena in una struttura dodecaedrica simboleggiante i 12 apostoli,
rappresentò nella Crocifissione la croce come sviluppo tridimensionale di un
ipercubo, e strutturò
Come tralasciare poi l'attualissima grafica computerizzata, che ha permesso la creazione di modelli visivi di superfici e composizioni geometriche che possono essere considerate vere e proprie forme d'arte(si pensi ai frattali).
Comunque, la matematica trova la sua più ampia espressione nell'architettura, che non può assolutamente prescindere da essa.
Senza la matematica e le sue formule, sarebbe stato impossibile per Mies Van der Rohe e gli altri innalzare i primi grattacieli, o per Le Corbusier progettare case in cemento armato con le pareti liberamente disposte.
E' proprio infatti l'avvento del cemento armato, insieme alla possibilità di valutare il peso insistente sui pilastri, che sostituiscono i muri portanti nelle strutture dell'architettura funzionale, a determinare una svolta nella progettazione delle strutture, che cambiano radicalmente aspetto.
L'architettura della Bauhaus propone infatti le forme delle strutture, i cui spessori sono calcolati in relazione alle forze portanti, in funzione del loro scopo, fa scomparire la facciata 'principale', in quanto ogni area, con la propria funzione, è ugualmente importante, e dà vita a quello che è stato definito International Style.
 Ancora impossibile sarebbe stato per Lloyd Wright progettare
e costruire la celebre 'Casa sulla cascata' senza adeguati calcoli strutturali.
Ancora impossibile sarebbe stato per Lloyd Wright progettare
e costruire la celebre 'Casa sulla cascata' senza adeguati calcoli strutturali.
La casa, che è sicuramente l'opera più significativa dell'architettura organica, è stata costruita utilizzando tutte le risorse della tecnologia moderna e i suoi materiali (vetro, ferro, cemento), e la maggiore particolarità consiste nell'apparire perfettamente naturale: tutto è stato studiato, calcolato, in modo da far sembrare la casa nata spontaneamente. Il corpo strutturale, di pietre a vista, è verticale, e si intreccia con le lastre orizzontali di cemento che arrivano oltre il limite della cascata, e tutto è in perfetto equilibrio, come arrivare a ciò senza l'ausilio della matematica?
QUANTITATIVE & QUALITATIVE VISION
In Henri Bergson's The Creative Mind: An Introduction to Metaphysics (1946) we can find a series of essays and lectures concerning the nature of intuition, explaining how it can be used as a philosophical method. Intuition is described as a method of 'thinking in duration' which reflects the continuous flow of reality.
The philosopher distinguishes between two methods of thinking, an intuitive one and a conceptual one, and because of this distinction he has developed a creed that goes against the positivistic one, based on a quantitative vision of the reality.
Bergson's intuitive method influences his own vision of time: he distinguishes in fact between two forms, pure time and mathematical time. Pure time is called by him real duration, and it is continuous and indivisible. Mathematical time is on the other hand measurable and divisible into units or intervals which do not reflect the flow of real time.
According to the philosopher it is impossible to analyze real time mathematically because measuring it would be like trying to create a break or disruption in the natural flow of time, like considering time as consisting of defined moments or intervals. Analyze real time mathematically would signify a misunderstanding of the real meaning of time, on the contrary the concept of real duration expresses the natural flow of time, and it can only be experienced by intuition.
In the quantitative representation of time, a succession of distinct states or events is presented as a spatialized form of time. Time is conceptualized as a sequence of defined events, rather than as an endless flow of experience in an indivisible continuity. The intellect analyzes time as having measurable duration, but the flow of real time can only be known by intuition.
According to Bergson, different kinds of knowledge originate from intellect and intuition. Scientific principles are intellectual, while metaphysical principles are intuitive. However, science and philosophy can be combined to produce knowledge that is both intellectual and intuitive.
Moreover, intuition is a mode of reflection, it isn't a single act but a fluidity of psychological actions.
 MATEMATICA &.LATINO?
MATEMATICA &.LATINO?
Come oggi l'inglese, per secoli e fino all'inizio del XIX secolo, il latino(chiaramente non il latino classico)è stato considerato la lingua ufficiale della comunicazione scientifica in Europa, tanto che anche dopo la diffusione del volgare la lingua usata dai 'colti' nei propri scritti rimaneva quella latina(esempi emblematici Galileo, che nei "Discorsi", che contiene un trattato sul moto ed era quindi destinato ad un pubblico di scienziati, alterna parti in latino a parti in volgare, Gauss, le cui opere maggiori sono scritte in latino, e Newton, che usava farsi tradurre da amanuensi le proprie opere dal latino all'inglese).
Ancora oggi, oltre che in ambiente ecclesiastico, si è conservato l'uso del latino nell'ambiente accademico in occasione di circostanze solenni, come lauree "ad honorem" o inaugurazioni dell'anno accademico.
Per quanto riguarda la letteratura antica, è molto più facile trovare brani a tema scientifico nei classici greci che in quelli romani, è risaputo infatti che, a differenza dei primi, i romani usarono la matematica unicamente per eseguire calcoli e misure(è di Cicerone la frase "I Greci tennero il geometra nella più alta considerazione e di conseguenza nulla compì fra loro progressi più brillanti della matematica. Noi invece abbiamo fissato come limite di quest'arte la sua utilità per misurare e per contare").

Importante eccezione è, però Tito Lucrezio Caro, di cui S. Gerolamo narra l'unica notizia biografica "Lucretius poeta nascitur, postquam a poculo amatorio in furorem versus et per intervalla insaniae aliquot libros conscripsisset, quem Cicero post emendavit, propria manu se interfecit aetatis anno suae XLIII".
(nasce il poeta T. Lucrezio, che dopo essere impazzito per un filtro d'amore e aver scritto alcuni libri negli intervalli della follia, che Cicerone pubblicò postumi, si suicidò quarantatreenne)
DE RERUM NATURA
 Lucrezio, che è stato spesso il definito promotore di una vera
e propria rivoluzione lucreziana, vive durante i turbolenti anni
della rivolta di Spartaco, della guerra in Gallia e probabilmente anche delle ostilità
fra Cesare e Pompeo, nel suo pensiero e nelle sue opere è riscontrabile perciò
l'aspirazione di un ritorno alla pace, da effettuarsi dopo un'opportuna
educazione dei concittadini.
Lucrezio, che è stato spesso il definito promotore di una vera
e propria rivoluzione lucreziana, vive durante i turbolenti anni
della rivolta di Spartaco, della guerra in Gallia e probabilmente anche delle ostilità
fra Cesare e Pompeo, nel suo pensiero e nelle sue opere è riscontrabile perciò
l'aspirazione di un ritorno alla pace, da effettuarsi dopo un'opportuna
educazione dei concittadini.
La strada che Lucrezio trova per affrontare i mali della vita è la dottrina di Epicuro, cantato come simbolo della ratio umana, che evidenzia le pecche della religione e della superstizione e prende coscienza della realtà dello stato umano.
Sul 'De rerum natura ', poema didascalico di natura scientifico-filosofica, (che è scritto in esametri e suddiviso in sei libri) si riflette, quindi, la concezione meccanicistica di Lucrezio e la sua volontà di proporre ai concittadini la dottrina di Epicuro, come mezzo per allontanare l'infelicità.
L'opera ha tre temi principali, l'antinomia fra ratio e religio (La ratio vista come quella chiarezza folgorante della verità «che squarcia le tenebre dell'oscurità», mentre la religio come cieca ignoranza e perciò causa dell'infelicità degli uomini), la concezione sul progresso (che non è positivo a priori, ma solo se libera l'uomo dall'oppressione, al contrario, se è fonte di degradazione morale, lo condanna duramente), e soprattutto la ripresa dei temi principali della dottrina epicurea, e cioè l'aggregazione atomistica e la 'parenklisis (che ribattezza 'clinamen'), la liberazione dalla paura della morte, la spiegazione dei fenomeni naturali, ritenuti meramente fisici e biologici.
Se nell'annoso dibattito sul rapporto e sull'eventuale possibile interazione di scienza e fede si cerca oggi di evitare quella netta separazione di cui la storia ci testimonia veri e propri scontri, e ne è un esempio l'enciclica 'Fides et ratio' di Giovanni Paolo II, Lucrezio è forse il sostenitore più acceso della tesi contraria.
Con parecchi secoli di anticipo su Marx e su Freud (La religione é un narcotico con cui l'uomo controlla la sua angoscia, ma ottunde la sua mente)
Lucrezio sostiene che la religione è l'"oppio del popolo", e ha portato l'uomo a compiere azioni imperdonabili accentuando ed estremizzando in questo caso le idee di Epicuro, che non aveva tendenze atee così marcate, ma auspicava un ritorno ad un culto più semplice.
Ma il De rerum natura nasce proprio da questa sua concezione che la religione è in grado di condizionare la vita di tutti gli uomini 'immettendo nel loro cuore un seme di paura' (la superstizione), e quindi dalla necessità di una speculazione scientifica per ovviare a questo timore, 'se gli uomini sapessero infatti che dopo la morte non c'è più nulla, smetterebbero di essere succubi della superstizione religiosa e dei timori che essa comporta '.
Nell'opera Lucrezio mira quindi a ricercare le cause e le leggi meccaniche dei fenomeni naturali onde eliminare l'ignoranza che le circonda, e che ne adduce la responsabilità a entità sovrannaturali;
dal punto di vista scientifico di particolare importanza ha soprattutto il primo libro, nel quale l'autore introduce la dottrina atomistica, (secondo cui tutto ciò che ci circonda è formato da piccolissimi granelli indivisibili, gli atomi, i semina rerum o genitalia corpora. Ogni pianta, pietra, uomo è formato da atomi, e così anche l'animo umano: ogni cosa, essendo un aggregato di atomi, è destinata a nascere e disfarsi, mentre gli atomi stessi sono immortali. Nel mondo, regolato dalle leggi meccaniche che governano le particelle elementari, c'è comunque spazio per la libertà: all'origine dell'universo c'è una deviazione del moto atomico, il clinamen, che ha dato il via alla formazione delle cose ed al gioco infinito della natura), e le teorie, materialiste e antiprovvidenzialiste, riguardo l'evoluzionismo (ogni specie vivente, secondo Lucrezio, è stata 'partorita' dalla Terra grazie al calore e all'umidità originari, ma le specie così prodotte sono mutate nel corso del tempo, quelle malformate si sono estinte, mentre quelle dotate degli organi necessari alla conservazione della vita sono riuscite a riprodursi.
Non riesco a concepire un vero scienziato senza una fede profonda.
La situazione può esprimersi con un' immagine: la scienza
senza la religione è zoppa; la religione senza la scienza è cieca.
Einstein Albert
E' molto diffusa l'idea secondo cui fede e scienza siano sfere totalmente autonome e in alcun modo conciliabili, ed episodi quali quello di Galileo ne testimoniano a favore. Certamente il rapporto di questi due ambiti è sempre stato segnato da forti dibattiti e aspre controversie, ma non bisogna fermarsi alle apparenze e credere che non sia possibile un dialogo, che in realtà è già iniziato da molto e testimone ne è l'enciclica di Papa Giovanni Paolo II, 'Fides et Ratio'.
Partendo dalla frase di Pasteur, che affermava che poca scienza allontana da Dio ma molta riconduce a lui, una semplice analisi può infatti dimostrare che in effetti scienza e fede non sono totalmente estranee l'una all'altra.
Come nascono fede e scienza? Sicuramente dalla volontà dell'uomo di conoscere, di capire, entrambe quindi si originano da quella caratteristica innata dell'uomo che è la curiosità, è il porsi continuamente domande su sé stesso e su ciò che lo circonda, instancabilmente e perennemente, domande a cui è difficile dare risposta e che pongono ogni uomo nella stessa condizione di incertezza e, forse, di instabilità.
'Non so chi mi ha messo al mondo, né cosa è il mondo, né cosa sono io stesso; sono in una terribile ignoranza di tutto: non so cos'è il mio corpo, i miei sensi, la mia anima, e persino questa parte di me che pensa ciò che dico, che riflette su di tutto e su di se stessa. Vedo questi spaventosi spazi dell'universo che mi racchiudono, ed io mi trovo in un angolo, senza sapere perché sono in questo luogo piuttosto che in un altro, né perché questo poco tempo che mi è concesso di vivere mi è dato ora piuttosto che in un altro momento di tutta l'eternità che mi ha preceduto e di tutta quella che mi seguirà. Tutto ciò che so è che debbo presto morire, ma ciò che ignoro di più è proprio questa morte che non saprei evitare' (Pascal)
Se alcuni si rassegnano alla propria 'terribile ignoranza' e accettano di seguire il flusso della vita senza farsi troppe domande, senza porsi troppi perché(sempre nelle parole di Pascal, gli uomini, non avendo potuto guarire la morte, la miseria, l'ignoranza, hanno risolto, per vivere felici, di non pensarci), tale condizione non è accettata da altri, la cui voglia di conoscere li porta a continue ricerche, continue analisi della realtà; è naturale quindi il porsi tali domande, ed è naturale come diretta conseguenza la nascita della fede come della filosofia, che tentano di dare risposte, di offrire il senso dell'esistenza, che gli uomini di ogni epoca hanno cercato, cercano e cercheranno.
Da sempre matematica e filosofia hanno seguito cammini che spesso si sono incontrati, è sbagliato allora considerarle due mondi a sé stanti, come oggi spesso si tende a fare?
Anche se oggi si propone infatti la teoria della separazione del mondo scientifico da quello umanistico, fin dall'antichità tali ambiti erano strettamente connessi, e probabilmente un libro come il Codice da Vinci, che ha scatenato incessanti dibattiti sul rapporto scienza/fede, non avrebbe fatto scandalo qualche anno fa, quando questo dibattito era già pienamente aperto.
 Ma facciamo un salto nel passato, un salto di circa 2300
anni, per scoprire che la scuola di Pitagora, una vera e propria scuola
filosofica, si interessava sistematicamente della matematica, e ne sono la
dimostrazione il loro motto, 'il numero è
il principio ', e la loro convinzione che tutti gli enti hanno una
caratteristica comune, la misurabilità, oltre che il teorema più 'famoso' fra
gli studenti, il teorema di
Ma facciamo un salto nel passato, un salto di circa 2300
anni, per scoprire che la scuola di Pitagora, una vera e propria scuola
filosofica, si interessava sistematicamente della matematica, e ne sono la
dimostrazione il loro motto, 'il numero è
il principio ', e la loro convinzione che tutti gli enti hanno una
caratteristica comune, la misurabilità, oltre che il teorema più 'famoso' fra
gli studenti, il teorema di  Pitagora, elaborato proprio dal caposcuola.
Pitagora, elaborato proprio dal caposcuola.
Andando oltre i pre-socratici, qualche secolo dopo lo stesso Platone confermò la convinzione che la realtà si potesse leggere in chiave matematica, affermando che anche se le sensazioni possono essere ingannevoli, la matematica offre d'altra parte certezze assolute ed inconfutabili('che 2 + 2 = 4 è sempre vero, lo è sempre stato e sempre lo sarà ').
Per poter utilizzare la matematica è però necessaria, oltre che l'intuizione, anche una successiva dimostrazione, e la mancanza di strumenti efficaci ha poi contribuito, nel Medioevo, a far passare in secondo piano l'intuizione platonico-pitagorica, che dopo secoli di assenza ha riacquisito una certa importanza solo nel Rinascimento, quando il modello cosmico qualitativo di Aristotele (strutturato sull'interazione dei quattro elementi, quali acqua, fuoco, terra e aria, contrapposto a quello platonico basato sui cinque solidi regolari), semplificativo e pertanto più logico, è stato rimesso in discussione.
Nel 1400 infatti, in opposizione ai canoni medievali, (Dante affermava che Aristotele fosse il 'maestro' di tutti gli altri), si sviluppa un vero e proprio anti-aristotelismo, che nel 1600 trova poi piena accoglienza con Galileo, che avrà possibilità e mezzi per 'misurare' la realtà, ciò, cioè, a cui non erano potuti arrivare Platone e Pitagora.
Il XVII secolo segna poi una svolta nella storia della matematica, la rivoluzione scientifica la propone infatti come strumento utile e fondamentale in ogni ambito culturale; se infatti nella sfera scientifica assume la funzione di strumento d'indagine della realtà, per quanto riguarda altri ambiti viene sfruttata come modello metodologico, anche se lo stesso Galileo, nel secolo precedente, aveva criticato questo secondo ruolo affermando che solo le caratteristiche quantitative della realtà, e non quelle qualitative, potessero essere studiate 'matematicamente', in termini matematici.
La reale differenza fra Galileo e Aristotele consisteva proprio nel fatto che, a differenza del secondo, l'inventore del telescopio rivolgeva la sua attenzione solo alle caratteristiche quantitative, come spesso è stato affermato, non si chiedeva il cosa e il come, ma il perché.
 Successivamente Cartesio ripropone invece la matematica come
metodo, affermando che, come
in matematica per risolvere un problema complesso è necessario scomporlo in
parti più semplici, altrettanto bisogna fare col pensiero, applicando cioè la
matematica in un ambito ad essa non proprio. Cartesio, matematico e filosofo,
propose dunque un metodo d'indagine matematico della realtà, ponendo sullo
stesso piano matematica e filosofia, inefficaci se prese indipendentemente
l'una dall'altra.
Successivamente Cartesio ripropone invece la matematica come
metodo, affermando che, come
in matematica per risolvere un problema complesso è necessario scomporlo in
parti più semplici, altrettanto bisogna fare col pensiero, applicando cioè la
matematica in un ambito ad essa non proprio. Cartesio, matematico e filosofo,
propose dunque un metodo d'indagine matematico della realtà, ponendo sullo
stesso piano matematica e filosofia, inefficaci se prese indipendentemente
l'una dall'altra.
Dopo Cartesio, l'applicazione del metodo matematico ad altri ambiti della realtà si deve a filosofi quali Spinosa, la cui opera più importante è "Etica dimostrata alla maniera della geometria", (in cui si possono trovare teoremi, definizioni, corollari), Hobbes, nell'ambito della politica, che sostiene che pensare non è altro che fare calcoli, Pascal, filosofo che inventa il primo prototipo di calcolatrice, e Leibniz, che la perfeziona e che, addirittura, grazie al contributo di Newton, può essere ritenuto il padre fondatore del calcolo infinitesimale.
Successivamente, figure di spicco nel dibattito filosofia-matematica, sono Hume, secondo cui la matematica rappresenta una "mera relazione tra idee" (l'emergere del predicato attraverso l'analisi del soggetto), e Kant, che afferma che la matematica ha per oggetto "giudizi sintetici a priori "(a priori in quanto non derivabili e inconfutabili empiricamente, sintetici in quanto implicano la costruzione di concetti e il conseguente ampliamento della conoscenza).
Necessario poi citare la filosofia del 900, secolo in cui la matematica assume un ruolo di fondamentale importanza. Filosofi quali Husserl e Russell ne ribadiscono infatti l'importanza, il primo schierandosi determinatamente contro l'irrazionalismo e analizzando il concetto di numero(esso, a suo avviso, deriva da un atto unitario della mente, il quale si dirige intenzionalmente su molteplicità di oggetti riuniti in "aggregato" specifico. In tal modo egli ricava per astrazione il concetto di "aggregato", assunto come relazione collettiva tra unità che originano una molteplicità; ne deriva che contando tali unità, si giunge al concetto di "numero"), che pone al centro del processo conoscitivo e definisce forma generale, dotata di autonomia e perciò rappresentativa del soggetto, mentre il secondo affermando che "La matematica non possiede soltanto la verità, ma anche la bellezza suprema, una bellezza fredda ed austera, come quella della scultura", che le assicura una certezza non smentibile(poiché poi, come credeva Platone, ciò che è vero è anche bello, la matematica stessa è una forma di bellezza).
Innegabile quindi l'esistenza del rapporto fra matematica e filosofia, qual è la differenza?
Può essere riassunta in una frase di Husserl.mentre la matematica si serve di numeri per svolgere espressioni, equazioni, sistemi e quant'altro, la filosofia si chiede se i numeri esistano o meno.
.la storia è testimone dei tempi, luce della verità, vita della memoria, maestra della vita, nunzia dell'antichità.
Cicerone
Anche se la statistica è lontana dall'essere il linguaggio esatto della realtà, l'utilizzo di grafici e l'analisi dei dati può rivelarsi utile e produttivo nell'analisi storica al fine di ottenere un'idea più concreta dei fenomeni storici.
Pur conservando un margine di errore ineliminabile, le stime statistiche ci offrono infatti una rappresentazione sintetica di molti fenomeni e la possibilità di confrontare nel tempo e nello spazio grandezze significative, come il flusso dei numeri demografici, scolastici o epidemiologici.
L'uso della statistica, definita 'un'arma meno logora e spuntata delle lamentazioni storiche e degli anatemi poetici' ci offre insomma uno specchio abbastanza fedele della storia, ed è per questo che non bisogna affatto sottovalutare l'importanza di numeri e percentuali nell'analisi dei dati storici.
Un esempio dell'uso della statistica nello studio della storia può essere quello dei grafici riguardanti il fenomeno dell'emigrazione, di cui l'analisi dei dati, delle cifre, ci può evidenziare determinate caratteristiche e dare un'immediata percezione dell'entità del fenomeno.
 Il rapido incremento della popolazione verificatosi tra la
fine dell'800 e i primi decenni del 900, fu parzialmente compensato dall'ondata
di emigrazioni: 'L'emigrazione europea costituì probabilmente il maggior
movimento di popoli che si sia mai registrato in tutta la storia umana',
coinvolgendo, secondo il demografo Armengaud, 34 milioni di persone, di cui 24
milioni si stabilirono definitivamente all'estero.
Il rapido incremento della popolazione verificatosi tra la
fine dell'800 e i primi decenni del 900, fu parzialmente compensato dall'ondata
di emigrazioni: 'L'emigrazione europea costituì probabilmente il maggior
movimento di popoli che si sia mai registrato in tutta la storia umana',
coinvolgendo, secondo il demografo Armengaud, 34 milioni di persone, di cui 24
milioni si stabilirono definitivamente all'estero.
Gli storici usano distinguere
il fenomeno dell'emigrazione europea in tre fasi, la prima dal periodo post
unitario alla Grande guerra, la seconda tra le due guerre mondiali, la terza
dagli anni 40 agli anni
Sicuramente le cause della massiccia emigrazione italiana, che ha toccato le punte massime nel primo ventennio del 900, vanno ricercate nei processi di modernizzazione della società, che hanno subito un'impennata dopo l'unificazione del 1861.
E'
emblematico infatti che il fenomeno abbia coinvolto 24 milioni di persone,
quando la stessa cifra corrisponde alla popolazione italiana al momento dell'unità
e al numero di persone rimaste all'estero(il numero dei rientrati corrisponde
con quello dei 10milioni partiti dagli anni
 Le cause vanno quindi ricercate in fenomeni post unitari
quali la crisi agraria che ha investito soprattutto il meridione tra ottocento
e novecento, le forti tasse imposte dai piemontesi ai contadini meridionali
subito dopo l'unificazione, le conseguenze del latifondismo, su cui si basava
l'economia del sud Italia, per generalizzare, la causa principale è stata
sicuramente la miseria.
Le cause vanno quindi ricercate in fenomeni post unitari
quali la crisi agraria che ha investito soprattutto il meridione tra ottocento
e novecento, le forti tasse imposte dai piemontesi ai contadini meridionali
subito dopo l'unificazione, le conseguenze del latifondismo, su cui si basava
l'economia del sud Italia, per generalizzare, la causa principale è stata
sicuramente la miseria.
A partire dall'unificazione, il fenomeno dell'emigrazione si è andato
incrementando, fino a raggiungere la media di 626 mila partenze annue negli
anni precedenti
Il flusso migratorio era composto soprattutto di giovani provenienti dall'Europa mediterranea e orientale, era diretto soprattutto verso le Americhe, e in particolare verso gli Stati Uniti, che acquisirono l'aspetto di una societ in rapido cambiamento, composta da diversi gruppi etnici, culturali e religiosi, e diventarono la meta di interi strati sociali provenienti soprattutto dall'Italia meridionale. Considerando come periodo campione il primo decennio del 900, dei 4 milioni di partenze più di due avevano come destinazione l'America; le mete, soprattutto quelle oltreoceano (Argentina, Uruguay), hanno attratto manodopera perchè scarsamente abitate.
Caratteristiche da evidenziare per identificare il prototipo di emigrante sono le seguenti:
![]() maggioranza di uomini rispetto
alle donne (circa cinque a uno nel periodo iniziale).
maggioranza di uomini rispetto
alle donne (circa cinque a uno nel periodo iniziale).
![]() prevalenza di contadini,
artigiani e muratori.
prevalenza di contadini,
artigiani e muratori.
![]() giovane età dell'emigrato
(maggioranza assoluta tra i quindici e i quarant'anni).
giovane età dell'emigrato
(maggioranza assoluta tra i quindici e i quarant'anni).
![]() diffuso analfabetismo (nel 1871
è al 90% nelle regioni meridionali).
diffuso analfabetismo (nel 1871
è al 90% nelle regioni meridionali).
Per quanto riguarda i territori di partenza, la prima fase ha coinvolto soprattutto il Nord Italia, mentre nei due decenni successivi il primato è passato alle regioni meridionali, e in particolare alla Sicilia (1.126.513 di partenze), e alla Campania (955.189 di partenze).
Importante evidenziare anche che gli emigrati settentrionali hanno scelto prevalentemente mete europee, mentre l'America ha visto arrivi numerosi soprattutto da parte dei meridionali.
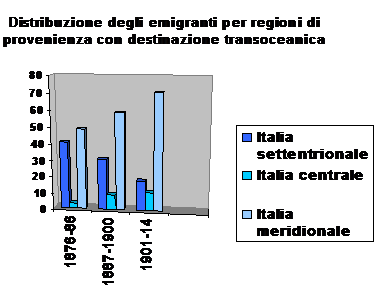
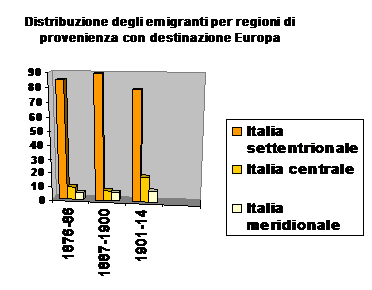
L'occupazione degli emigrati è stata soprattutto nella costruzione di strade e di ferrovie, in impieghi in fabbrica o in miniera, e nella lavorazione delle terre(in particolare in Argentina e in Brasile, nelle fazendas).
L'emigrazione era vista con favore dal Governo, che perciò inizialmente non fece nulla per assistere e per tutelare in qualche modo gli emigranti. Tale atteggiamento scaturiva dal presupposto che le rimesse degli emigranti sarebbero servite per affrontare e risolvere i secolari problemi del Mezzogiorno e delle altre zone depresse della penisola, e dal fatto che la mancanza di manodopera fece lievitare le paghe dei braccianti agricoli.
Successivamente però il fascismo, con la sua politica demografica, ha in parte ridimensionato e limitato gli espatri, la media di scese infatti a 52 mila nel periodo tra il 1933 ed il 1937, ma il numero di trasferimenti in paesi europei rimase perlopiù invariato.
Impossibili da tralasciare sono alcune conseguenze negative che hanno accompagnato l'emigrazione, a cui è infatti strettamente collegato il fenomeno dell'integrazione, argomento più che attuale.
Come oggi è infatti l'Italia ad essere teatro di immigrazione e troppo spesso di discriminazione, in passato sono stati proprio gli italiani a partire con poche valigie e tante speranze ed essere talvolta accolti da disprezzo e diffidenza, e ciò ci dovrebbe far riflettere sul significato e sull'importanza dell'accettazione della diversità. Gli episodi di xenofobia del passato, come quello di Sacco e Vanzetti, anarchici italiani condannati a morte senza alcuna colpa, di Aigues Mortes, in Francia, dove nel 1893 sono stati linciati una cinquantina di italiani, o quella di New Orleans, dove undici siciliani sono stati linciati con l'accusa di appartenere alla mafia, sono simili a quelli più attuali, dove protagonisti sono gruppi razzisti che dimenticano il valore della fratellanza.
Solo lo scienziato è vero poeta, ci dà la luna, ci promette le stelle, ci farà un nuovo universo se sarà il caso.
Allen Ginsberg

Anche nel caso delle scienze, il rapporto con la matematica è fondamentale. Se poi ci riferiamo alla geografia astronomica, e in particolare all'astronomia, è impossibile non considerare l'estrema importanza dell'apporto matematico.formule matematiche hanno permesso la costruzione di satelliti artificiali e di sonde che ci forniscono informazioni su stelle e pianeti, calcoli matematici ci consentono di stabilire le distanze nello spazio, ancora dati matematici, convertiti poi in immagini o sistemati in grafici, ci hanno chiarito e ci chiariscono sempre più i grandi misteri dell'universo.
Dalla legge di Hubble, secondo cui gli astri si stanno allontanando con velocità proporzionale alla loro distanza, allo studio degli spettri, ottenuti mediante raggi luminosi provenienti dalle stelle, dalle onde magnetiche alle misure astronomiche, non si può prescindere dalla matematica e dalla fisica per un approfondito studio della geografia astronomica, e sono infiniti gli esempi che si potrebbero riportare.
E' però particolarmente
interessante capire come la matematica sia stata utile al fine di ottenere la
misura della circonferenza terrestre, ancor più se ci si riferisce alla
matematica del

Molti sono stati i
tentativi di misurare la circonferenza terrestre fin dall'antichità, ma uno fra
i più validi, soprattutto perché nonostante fosse il primo si è avvicinato
molto alla misura reale, è stato proprio quello di Eratostene da Cirene (276 -
Basandosi sui dati allora a disposizione
![]() La distanza fra Alessandria e
Siene, che riteneva essere posizionate sullo stesso meridiano, valutata di
circa 5000 stadi (1 stadio=157,5m)
La distanza fra Alessandria e
Siene, che riteneva essere posizionate sullo stesso meridiano, valutata di
circa 5000 stadi (1 stadio=157,5m)
![]() La differente altezza raggiunta
a mezzogiorno del 21 Giugno, solstizio d'estate, nelle due città. A Siene infatti
il sole è sulla verticale(il sole arriva allo zenit, i raggi sono cioè
perpendicolari al suolo), mentre ad Alessandria formano un angolo di 7°
La differente altezza raggiunta
a mezzogiorno del 21 Giugno, solstizio d'estate, nelle due città. A Siene infatti
il sole è sulla verticale(il sole arriva allo zenit, i raggi sono cioè
perpendicolari al suolo), mentre ad Alessandria formano un angolo di 7°
E rifacendosi al teorema di Talete, secondo cui gi angoli corrispondenti (formati da due rette parallele tagliate da una trasversale) sono uguali, determinò l'angolo al centro che gli permise di impostare la seguente proporzione:
7° : 360° = 5.000 stadi : x
Da cui la circonferenza
risultò pari a 257.142 stadi, e cioè circa 40.500km, che si distanzia dalla
misura reale di poco meno di
Successivamente Posidonio utilizzò lo stesso metodo utilizzando però la distanza fra Alessandria e Rodi e valutando la differente altezza della stella Canopo sulle due città.
A causa della compensazione di alcuni errori il risultato, di circa 240.000 stadi, si discostava di poco da quello del precedente.
Successivamente
risultarono meno convincenti i tentativi di alcuni matematici arabi, che nel
VII secolo d.C. valutarono la circonferenza pari a 43.000km, o Snell, olandese
che con la tecnica della triangolazione ottenne la misura di quasi

Come può accadere che la matematica,
pur essendo in definitiva
un prodotto del pensiero umano
indipendente dall'esperienza,
si adatti in modo così ammirevole
agli oggetti nella realtà.
Albert Einstein (1920)
THE END
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Fisica |  |
| Lezioni Statistica |  |