 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1716 | Gradito: |
Leggi anche appunti:Derivate parzialiDERIVATE PARZIALI DEFINIZIONE Sia una funzione di due variabili e sia Differenziale di una funzioneDifferenziale di una funzione 1. Dimostrazione Il piano cartesianoIl piano cartesiano Le coordinate cartesiane Il piano cartesiano è un |
 |
 |
Matematica: non solo numeri
Sebbene sia molto diffusa ai giorni nostri l'idea che considera la matematica una materia scolastica arida, troppo astratta, lontana dalla vita quotidiana se non addirittura inutile, l'atteggiamento che tende semplicemente ad ignorarla è a mio parere sbagliato. Questa opinione nasce probabilmente dai metodi di insegnamento con i quali si affronta questa disciplina. Essa non è solamente "far di conto". Spesso la scuola privilegia per lo più l'aspetto tecnico del calcolo che è certamente essenziale ma non è il fine della matematica, ne è uno degli strumenti.
La matematica in origine è la scienza che si occupa dei calcoli e delle misure, nasce probabilmente quando l'umanità passa dalla fase di cacciatore-raccoglitore a quella di agricoltore-allevatore, quando cioè sorsero problemi relativi alla divisione del territorio e all'amministrazione razionale delle risorse. Attualmente invece si può parlare di matematica attuariale - che ha per oggetto la valutazione attuale di impegni futuri relativi alle assicurazioni sulla vita- e di matematica finanziaria - che si occupa di problemi di capitalizzazione, calcolo di rendite, ammortamenti.- Essa quindi si propone di indagare il mondo empirico e di fornire un'organizzazione razionale dei fenomeni naturali. Un'indagine che, tuttavia, dalla realtà riceve solamente il primo "impulso", ma i risultati a cui giunge prescindono dal mondo esterno; Anche studi puramente astratti, e non solo quelli motivati da esigenze scientifiche e tecniche, si sono dimostrati di grandissima utilità. La scoperta delle sezioni coniche (parabole, ellissi e iperboli) che tra l'altro venne abbandonato per diversi anni per scarsità di interessi pratici, hanno poi reso possibile in secoli recenti la moderna astronomia, la teoria del moto dei proiettili e la legge gravitazionale universale.
Un esempio molto semplice e di carattere pratico che dimostra come l'opinione che giudica la matematica "lontana dalla quotidianità" sia infondata, potrebbe essere quello di trovare le altezze o le distanze di oggetti inaccessibili o difficilmente accessibili mediante misure eseguite su oggetti facilmente accessibili, basandoci sul teorema di Talete.
Pensiamo di avere un grande piazzale in cui è innalzata un'asta molto alta e vi è pure un paletto verticale poco più alto di un metro e pensiamo di dover misurare con un normale metro da sarto l'altezza dell'asta. Una persona del tutto digiuna di matematica pensa che sia necessario arrampicarsi fino alla cima dell'asta; in realtà volendo trovare 1'altezza dell'asta senza salire così in alto basta misurare l'altezza del paletto, la lunghezza dell'ombra del paletto in una data ora del giorno e la lunghezza dell'ombra dell'asta alla stessa ora. E' chiaro che il rapporto tra l'altezza dell'asta e quella del paletto sarà uguale al rapporto tra le lunghezze delle due ombre. Per esempio, se il paletto era alto un metro e mezzo e la sua ombra era lunga ottanta centimetri, mentre 1'ombra dell'asta era lunga otto metri, 1'asta sarà alta quindici metri.
Oggetto dello studio matematico è dunque la realtà. A partire da una situazione problematica reale, dopo averne estratto gli elementi essenziali (o le variabili se vogliamo), si cerca di individuare le relazioni intercorrenti tra essi e di tradurli in legami di natura matematica (equazioni o funzioni per esempio) , pervenendo così ad una modellizzazione della realtà sensibile.
Ed è proprio in questo senso che si arriva ad una organizzazione razionale dei fenomeni naturali, il modello matematico, risultato dell'astrazione, ci permette di capire meglio il problema da risolvere in modo da potere agire su di esso e poterlo modificare di conseguenza. Questa caratteristica della matematica ha fatto sì che nel corso della storia diverse scienze hanno influenzato il suo sviluppo e sono state a loro volta influenzate da essa. Problemi di fisica o di ingegneria hanno costituito spesso il punto di partenza per la riflessione matematica. D'altra parte conclusioni e concetti matematici hanno permesso la risoluzione di molti problemi di tipo economico, finanziario, fisico, ingegneristico ecc. Possiamo parlare quindi dell'applicazione matematica alle altre scienze oppure di matematica applicata che ha consentito il raggiungimento di importanti sviluppi e progressi in vari ambiti.
Spesso i mezzi di informazione sono portati a mettere in evidenza più l'importanza dei macchinari o degli strumenti tecnologici che non l'intelligenza necessaria, direttamente o indirettamente, per progettarli e per farne un buon uso. Ed è forse anche per questo che ultimamente assistiamo ad un divario sempre più profondo e in continuo aumento tra la persona comune e il mondo delle scienze.
Ho accennato all'applicazione matematica in campo economico, di seguito cercherò di presentare qualche esempio che possa rafforzare la mia analisi.
Economia:
"il vero economista deve possedere una rara combinazione di talenti. [..] in qualche misura deve essere un matematico, uno storico, un uomo di stato ed un filosofo"
John Maynard Keynes
Il primo rapporto con la matematica risale ai calcoli di natura commerciale con cui i mercanti dell'antichità avevano a che fare quotidianamente. Questo processo divenne più consistente con i calcoli di natura finanziaria necessari ad usurai e banchieri, e si sviluppa con delle applicazioni dell'aritmetica che oggi chiamiamo computisteria, che assume rilevanza pratica nel momento in cui una qualsiasi persona investe i suoi risparmi, scorpora l'Iva, emette una fatture o persino quando compila la dichiarazione dei redditi.
Durante l'alto medioevo i mercanti svilupparono un metodo per fare "quadrare i conti" delle loro imprese e tenere sotto controllo le entrate e le uscite. È in Italia, probabilmente nella seconda metà del XIII secolo, che si sviluppa il sistema della contabilità tenuta con il metodo della partita doppia che tutt'oggi è alla base della gestione dei conti delle aziende. Una descrizione del suo funzionamento fu pubblicata da Luca Pacioli in un capitolo della sua enciclopedia matematica.
Ora, fino a quando le esigenze di carattere pratico del commercio sono state soddisfatte dall'aritmetica, i rapporti tra la matematica e l'economia sono stati superficiali e costanti; I mercanti avevano bisogno di tenere sotto controllo e in ordine i loro conti e i matematici avevano gli strumenti per farlo. La progressiva trasformazione dei concetti economici in una scienza sociale fa emergere sia un rapporto più profondo tra l'economia e la matematica sia una nuova professione: l'economista, con il compito di gestirla.
L'economista, che in molti casi non ha mai avuto modo di utilizzare la partita doppia, prima di assumere questa qualità ha dovuto studiare il calcolo differenziale, l'algebra lineare, la teoria della probabilità e la statistica. Deve quindi coltivare una conoscenza approfondita della matematica necessaria per la costruzione, la comprensione e l'uso dei modelli quantitativi. La sua attività diventa in un certo senso simile a quella di un ingegnere, si sforza cioè di rendere concreti concetti di una disciplina che ha raggiunto lo status di scienza.
La matematica vista all'inizio come un modo per esemplificare i concetti economici, diventa gradualmente un linguaggio in cui formulare e comunicare la teoria economica, e allo stesso tempo uno strumento per dimostrare la coerenza logica della teoria stessa.
La competenza matematica dei primi studiosi di economia sono probabilmente racchiusi entro l'aritmetica necessaria alla contabilità e alla computisteria, e poiché l'economia si occupa di prezzi e di valori, la riflessione non può fare a meno dell'uso dei numeri, ma questo uso è soprattutto esemplificativo: serve cioè a convincere il lettore che i "conti tornano". Gli studiosi cercano di scoprire "le leggi" di comportamento dei sistemi economici che occorre spiegare e l'aritmetica contribuisce in maniera determinante a questo processo.
Richard Cantillon per esempio, che nel suo Saggio sulla natura e sul commercio in generale (1755), per illustrare come alla stessa quantità di lavoro di un uomo possa corrispondere un potere di acquisto diverso, usa le proporzioni:
Ad esempio, se la giornata di un uomo è pagata un' oncia d'argento e quella di un altro uomo
è pagata soltanto mezza oncia, allora il primo ha accesso al doppio di prodotti della terra che il secondo.
Adam Smith, considerato il padre della scienza economica, utilizza invece la moltiplicazione e la divisione in "Indagine sulla natura e le cause della ricchezza delle nazioni" (1776), per chiarire come la specializzazione possa aumentare la produttività di un lavoratore:
un lavoratore non specializzato [.] non riuscirebbe certamente a produrre venti spilli in un giorno. [.]
Ma laddove dieci di questi lavoratori [.] sono impiegati in due o tre mansioni diverse [.], essi riescono a produrre oltre 48.000 spilli al giorno. Ciascuno di essi, dunque, è come se producesse 4.800 spilli al giorno.
Quindi Catillon dimostra che alla stessa quantità di lavoro può corrispondere un salario diverso, Smith spiega che una diversa organizzazione del lavoro può incidere in positivo sulla produttività del lavoro, ma queste due proposizioni possono essere enunciate senza usare la matematica. Tuttavia, il ricorso all'esempio aritmetico fa emergere l'argomento con superiore chiarezza. I "conti tornano", in quanto a ciò che si afferma si può dare un riscontro numerico che fornisce la certezza e la coerenza del discorso.
Lo strumento matematico assunse rilevanza maggiore con l'avvento della corrente marginalista, si iniziò a parlare di forma matematica con contenuto economico, una tecnica che permette di evitare quell'uso negativo della dialettica per esprimere teorie e concetti economici.
L'utilità marginale:
Concetto cardine dei marginalisti fu l'utilità marginale.
In generale l'aggettivo "marginale" indica il tasso di variazioni del valore di una funzione economica corrispondente alla variazione unitaria della variabile. L'innovazione principale dei marginalisti fu fondato sull'idea che il valore di un bene è misurabile con la sua "utilità marginale" anziché con il lavoro necessario per la sua produzione, la quale utilità marginale può essere definita come l'incremento del livello di utilità ricollegabile ad aumenti marginali nel consumo del bene. In altra parole l'utilità marginale non è altro che l'utilità apportata dall'ultima unità o dose consumata di un bene. Con il seguente esempio si dimostra come questo concetto abbia permesso di chiarire alcuni punti sul valore dei beni:
supposto che il soggetto abbia a disposizione cinque secchi di acqua, il primo lo impiegherà per dissetarsi e ha quindi per lui la massima utilità, il secondo gli servirà per cucinare i cibi e quindi ha un minore grado di utilità rispetto al primo, il terzo gli servirà per la pulizia personale, il quarto per lavare la biancheria e il quinto per innaffiare i fiori. Ogni secchio è uguale all'altro, ma l'importanza (cioè il valore) che il soggetto annette all'acqua che ha a disposizione è data dall'ultimo secchio! Infatti, se per un motivo qualsiasi i secchi diventassero quattro, il soggetto non rinuncerà certo a bere, bensì ad innaffiare i fiori, cioè a soddisfare il bisogno meno intenso.
Il soggetto agisce quindi valutando le possibilità pratiche che derivano dall'avere una dose in più o in meno di un certo bene. In altri termini considera l'utilità marginale del bene stesso.
Marginalità e derivata:
I marginalisti applicano l'analisi differenziale all'economia, infatti il concetto di marginalità è riconducibile al concetto di derivata; con l'esempio seguente, prendendo in esame l'utilità marginale, illustrerò il legame intercorrente tra marginalità e concetto di derivata:
supponiamo che un individuo stia consumando un bene x da cui riceve un'utilità u=U(x)
e che gli venga data la possibilità di consumare un'unità in più di quel bene. Di quanto varierà la sua utilità in conseguenza a questa variazione nel consumo? Qual è quindi il contributo al margine di quell'unità consumata in più all'utilità complessiva del consumatore?
Supponiamo che la variazione nel consumo del bene x aumenti di Δx unità, passando da x a x + Δx , di conseguenza l'utilità del consumatore passa da u=U(x) a u'=U(x + Δx) con una variazione pari a Δu u'-u. Ora, se facciamo il rapporto tra la variazione dell'utilità e la variazione della quantità del bene x che l'ha causata otteniamo il cosiddetto "saggio di variazione dell'utilità" che misura di quanto varia, in media, l'utilità per ogni unità consumata in più del bene x. Possiamo formalizzare il concetto del saggio di variazione dell'utilità come segue:

Da un punto di vista matematico, il saggio di variazione dell'utilità non è altro che il rapporto incrementale della funzione di utilità U(x). A questo punto se prendiamo in considerazione variazioni arbitrariamente piccole nel consumo del bene x, ovvero se facciamo tendere Δx a 0 abbiamo:

Che ci dà la definizione di quella che viene chiamata l'utilità marginale del bene. In termini matematici quindi, essa non è altro che la derivata della funzione di utilità in corrispondenza al consumo del bene x e misura di quanto aumenta l'utilità se variamo in maniera infinitesimamente piccola il consumo del bene x.
La nozione di marginalità caratterizza una serie di valori economici. Oltre all'utilità marginale che è stato un concetto cardine del pensiero marginalista, e che fornisce indicazione sul valore del bene come si è avuto modo di verificare, è di altrettanta importanza la marginalità del costo.
Con costo marginale si intende l'incremento che subiscono i costi totali in seguito all'aumento della produzione di un'unità.
I costi totali sostenuti da un'impresa per la produzione ottenuta è la somma dei costi fissi (cioè quelli che non variano al variar della quantità prodotta, sono quindi relativi a fattori produttivi fissi) e dei costi variabili (cambiano in funzione della quantità prodotta, è il caso delle materie prime).
![]()
Se indichiamo con q la quantità prodotta e con C il costo complessivo, risulta che C è in funzione di q ovvero è C(q).
Supponiamo che l'azienda aumenti la propria produzione di h unità, essa passerà quindi dalla produzione di q alla produzione di q +h spendendo una somma pari a :
![]()
Il rapporto:

tra la spesa sostenuta per produrre la quantità h e la quantità h stessa, si chiama variazione del costo totale per produrre un'unità di h. Matematicamente, esso non è altro che il rapporto incrementale della funzione del costo C(q).
A questo punto se prendiamo in considerazione incrementi arbitrariamente piccoli nella produzione, ovvero se facciamo tendere h a 0 abbiamo:
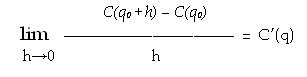
che se esiste ed è finito, ci dà la definizione del "costo marginale". In termini matematici, il costo marginale non è altro che la derivata prima della funzione del costo, e misura di quanto aumentano i costo totali se variamo in maniera infinitesimamente piccola la quantità prodotta.
Anche in questo caso il calcolo del costo marginale è di rilevanza fondamentale se consideriamo che un produttore razionale dovrebbe sempre evitare di produrre e vendere un'unità in più se il costo marginale dovesse superare il prezzo di mercato dell'unità prodotta.
Meno evidente invece potrebbe sembrare un possibile intreccio tra le scienze matematiche e quelle umanistiche, e in particolare la presenza di concetti matematici nel campo letterario.
Letteratura
Molto interessante come il padre della letteratura italiana, Dante Alighieri, abbia saputo cogliere e interpretare in maniera poetica e originale il potere magnifico e spesso metaforico delle scienze, e come strutture logico-razionali siano alla base di alcuni canti della "Divina Commedia " e più in generale del pensiero dantesco.
Paradiso, XVIII, 13-15
|
"O cara piota mia, che sì t'insusi, che come veggion le terrene menti non capere in triangol due ottusi, |
O cara radice della mia famiglia, che t'innalzi così in alto, che, come la mente dei mortali vede che due angoli ottusi non possono essere contenuti in un triangolo, |
|
così vedi le cose contingenti anzi che sieno in sé, mirando il punto a cui tutti li tempi son presenti; |
con la stessa chiarezza discerni le cose che possono essere o non essere prima che esistano in atto contemplando la divina essenza, il punto in cui tutti i tempi sono presenti |
Siamo all'inizio del canto XVII, Cacciaguida, nei due canti precedenti, racconta a Dante com'era la città di Firenze dei suoi tempi, descrivendola come una città pacifica e così diversa da quella dell'età del Sommo Poeta, e rispondendo ad alcune sue domande, Cacciaguida accenna allo scontro avvenuto tra due nobili famiglie che diede origine alla divisione tra Guelfi e Ghibellini. A questo punto Dante sente il vivo desiderio di conoscere la verità intorno alle future vicende della propria vita. Beatrice e Cacciaguida si accorgono di questo desiderio, e la donna lo invita ad esprimerlo, non perché esso sia a loro ignoto, ma perchè egli si abitui a manifestare ciò che desidera. Dante prega allora il trisavolo, poiché egli vede in Dio con certezza matematica le cose che dovranno avvenire, di rivelargli gli eventi della sua vita futura.
In questi versi Dante spiega che Cacciaguida può vedere gli eventi prima che siano accaduti con la stessa chiarezza con cui la mente umana capisce che un triangolo non può avere due angoli ottusi. L'assoluta certezza che hanno i beati su quello che dicono riguardo gli eventi futuri è pari ad una indubitabile certezza geometrica.
Il riferimento:
Dante si riferisce al teorema 17esimo del I libro degli "Elementi" di Euclide, la dimostrazione che un triangolo non può avere due angoli ottusi.
|
|
Considerate un triangolo ABC e un suo lato qualsiasi, ad esempio BC. Tracciate la retta r parallela al lato BC e passante per A. Tale retta è unica per il quinto postulato di Euclide. I due angoli 2 e 2' e i due angoli 3 e 3' sono uguali in quanto sono alterni interni rispetto alle parallele r e BC tagliate da AB. Ne segue che: E sapendo che, in quanto formano angolo piatto 1+2+3'= 180 Allora : 1+2+3 = 180 la somma dei tre angoli del triangolo è uguale a un angolo piatto cioè è uguale a 180°, e in base a questa conclusione ogni triangolo può avere tutt'al più un solo angolo ottuso |
Paradiso, XXVIII, 91-93
|
L'incendio suo seguiva ogne scintilla; |
Ogni Spirito Angelico rimaneva nel suo cerchio, ed erano tanti che il loro numero ascende a molte migliaia, ancora più che il numero che si ottiene raddoppiando via via le caselle del gioco degli scacchi. |
La situazione è la seguente, i canti XXVIII e XXIV del paradiso sono dedicati alla dottrina degli angeli. Dante osserva gli Spiriti Angelici che presiedono i novi cieli del Paradiso, disposti secondo nove cerchi concentrici in movimento: da ognuno di essi, come da un pezzo di ferro incandescente, si stacca un numero enorme di scintille. Il poeta è di fronte l'esigenza di esprimere un numero grande, grandissimo, tendente ad infinito, ma la sua genialità artistica non gli permette di usare la parola semplice "infiniti", così sceglie di usare una espressione più esatta tratta proprio dalla scienza dei numeri.
Il riferimento:
l'episodio a cui il poeta fa riferimento è una storia orientale di carattere matematico, seconda la quale l'inventore degli scacchi avrebbe chiesto al sovrano di Persia, cui aveva fatto dono del nuovo gioco passatempo, in premio alla sua invenzione, un chicco di grano per la prima casellina, il doppio (cioè due chicchi) per la seconda, il doppia ancora (ovvero quattro) per la terza casellina e così via fino alla sessantaquattresima casellina, visto che la scacchiera ha sessantaquattro ( 8x 8 ) caselle.
Il calcolo del numero di chicchi, che l'inventore avrebbe dovuto ricevere, è risolvibile se si conoscono le progressioni geometriche.
Una progressione geometrica è una successione di numeri,
tali che il quoziente tra ciascuna di essi e il precedente sia costante.
I chicchi sulle caselle numerate da
![]()
E sapendo che in questo caso è di 2, Si ottiene che il numero dei chicchi di grano che l'inventore avrebbe dovuto ricevere è:
![]()
Un numero praticamente illeggibile in grado di sottolineare una quantità enorme.
Paradiso, XXXIII, 133-138
|
Qual' è 'l geometra che tutto s'affige per misurar lo cerchio, e non ritrova, pensando, quel principio ond'elli endige |
Come lo studioso di geometria si concentra con tutte le sue facoltà mentali per risolvere il problema della quadratura del cerchio, e non riesce a trovare quel principio di cui avrebbe bisogno |
|
Tal ero io a quella vista nova; veder voleva come si convenne l'imago al cerchio e come s'indova; |
tal ero io dinanzi a quella straordinaria visione, che invano volevo capire come l'effigie umana si adattasse alla forma del cerchio e potesse trovarvi luogo; |
Siamo nell'ultimo canto del Paradiso, e quindi dell'intero poema. Il canto si apre con la preghiera da parte di san Bernardo alla Vergine, affinché interceda a favore di Dante, in modo che quest'ultimo possa elevarsi alla visione diretta di Dio. la preghiera viene esaudita e a Dante viene rilevata l'unità dell'universo e svelati i principali dogmi del cristianesimo (quello della trinità e dell'incarnazione di Cristo)
I versi riportati sono relativi alla situazione, sicuramente più solenne, in cui si trova Dante. La "Vista nova" cui il poeta si trova davanti è Dio stesso. Al potenziarsi della vista del pellegrino, Padre Figlio e Spirito Santo si sono mostrati sotto forma di tre cerchi di diverso colore e di raggio uguale. C'è quindi il tentativo di tradurre in forme geometriche il mistero della Trinità. All'interno del secondo cerchio, generato dal primo come luce riflessa, compare la figura umana dello stesso colore del cerchio; ciò sta a significare la duplice natura, divina e umana, di Cristo. Ecco raffigurato quindi il mistero dell'incarnazione. Queste trasformazioni in termini geometrici e figurativi testimoniano la volontà di conoscenza intellettuale da parte dell'uomo-Dante e nello stesso tempo il limite di tale conoscenza, poiché Dante, quando cerca di capire come l'immagine umana si adatti alla forma del cerchio e trovi posto in essa, viene a trovarsi nella stessa condizione dello studioso di geometria che non riesce a risolvere il problema della quadratura del cerchio.
Il riferimento:
la quadratura del cerchio è un classico problema di matematica, di geometria più precisamente.
Il problema è quello di costruire, usando solo riga e compasso, un quadrato con la stessa area di un dato cerchio. Questo problema ha tenuto occupati i matematici per lungo tempo e non fu che nel 1882 che l'impossibilità del problema venne rigorosamente provata.
La costruzione di un quadrato avente la stessa area di un cerchio di raggio unitario richiede la costruzione del numero π , il quale però è un numero trascendente, non-algebrico e quindi non-costruibile. La trascendenza di π fu dimostrata da Ferdinand von Lindemann, sistemando in modo definitivo l'annosa questione della quadratura del cerchio.
Così la futilità dell'impegno di diversi matematici nella ricerca della soluzione del suddetto problema, ha portate all'uso del termine in diversi ambiti, semplicemente per indicare una situazione senza speranza, senza significato oppure un'impresa vana.
Spesso i letterati sono stati attratti da alcuni concetti matematici proprio per potere comunicare le proprie idee ed esprimerle in maniera più rigorosa. È il caso di Alessandro Manzoni nei promessi sposi (capitolo ottavo). Lo scrittore vuole comunicare come la diffusione di un segreto narrato di amico in amico cresce secondo un modello esponenziale fino a diventare noto a tutte le persone di un ambiente : è in base a questo principio che la notizia di fuga di Lucia insieme alla madre si diffonderà. Il Manzoni esprime ironicamente questa legge in termini letterari.
Una delle più gran consolazioni di questa vita è l'amicizia, e una delle consolazioni dell'amicizia è quell'avere a cui confidare un segreto. Ora, gli amici non sono a due a due come gli sposi; ognuno generalmente parlando, ne ha più d'uno: il che forma una catena di cui nessuno potrebbe trovare la fine. Quando dunque un amico si procura quella consolazione di deporre un segreto nel seno d'un altro, dà a costui la voglia di procurarsi la stessa consolazione anche lui. Lo prega, è vero, di non dir nulla a nessuno; e una tal condizione, chi la prendesse nel senso rigoroso delle parole, troncherebbe immeditamente il corso delle consolazioni. Ma la pratica generale ha voluto che obblighi soltanto a non confidare il segreto se non a chi sia un amico ugualmente fidato e imponendogli la stessa condizione. Così, d'amico fidato in amico fidato, il segreto gira e gira per quell'immensa catena, tanto che arriva all'orecchio di colui o di coloro a cui il primo che ha parlato intendeva appunto di non lasciarlo arrivar mai. Avrebbe però ordinariamente a stare un gran pezzo in cammino, se ognuno non avesse che due amici: quello che gli dice e quello a cui ridice da tacersi ma ci sono degli uomini privilegiati che gli contano a centinaia, e quando il segreto è venuto a uno di questo uomini i giri divengon sì rapidi e sì moltiplici, che non è più possibile di seguirne la traccia.
Un'altra esperienza -questa volta contemporanea- molto significativa in questo campo è l'Oulipo ( Ouvroir de littérature Potentielle) fondato in Francia dallo scrittore Raymond Queneau insieme al matematico François Le Lionnais nell'ambito dello strutturalismo. "l'officina della letteratura potenziale" riunisce un gruppo di letterati interessati alle scienze esatte e matematici appassionati di letteratura, allo scopo di dare vita a originali e divertenti opere letterarie, costruite su strutture matematiche e tecniche di struttura vincolata.
Italo Calvino fu uno dei membri dell'Oulipo. Sebbene la carriera dello scrittore si muove in ambiti strettamente letterari, la passione scientifica non lo ha mai abbandonato ed è stato una delle più significative figure che nel Novecento si sono abbattute per una intensa collaborazione tra i due rami del sapere. Per Calvino la scienza farà conoscere alla letteratura nuovi campi in cui l'immaginazione potrà spaziare, e il modello del linguaggio matematico salverà lo scrittore dal limite delle parole nella rappresentazione della realtà.
La stagione scientifica di Calvino punta quindi ad una innovazione scientifica della letteratura, in particolare, con gli incisivi racconti delle Cosmicomiche, egli riesce a fornire un esempio di una nuova letteratura che coopera con la scienza e che da essa trae spunti fantastici.
Calvino fu particolarmente attratto dalla combinatoria, cui metodi hanno dato alla narrativa risultati non trascurabili nell'ambito delle ricerche dello strutturalismo. Lo scrittore con, Il castello dei destini incrociati, riesce a passare dalla combinatoria delle possibilità del reale a quella dei possibili narrativi, dando luogo ad una serie potenzialmente infinita di storie ricavate dalle figure di un mazzo di tarocchi.
Informatica:
l'informatica si appoggia alla matematica in modo rilevante, sono quindi due discipline che interagiscono tra loro in maniera continua. Negli ultimi tempi, lo sviluppo delle tecnologie informatiche ha modificato in profondità le pratiche associate al calcolo, sia le pratiche quotidiane e sociali che le pratiche scientifiche. La maggior parte degli algoritmi di calcolo, il cui apprendimento un tempo occupava la maggior parte del tempo scolastico, si trovano oggi già installati nelle calcolatrici più semplici. A sua volta, la matematica fornisce concetti fondamentali su cui l'informatica si basa nelle sue applicazioni.
Nel corso di questo anno si è visto come l'introduzione di una organizzazione di dati basata su concetti matematici abbia reso più semplice ed efficace la trattazione dei dati.
Si parla precisamente del modello relazionale di database che permette di rappresentare i dati sotto forma di tabelle.
Il modello relazionale è stato proposto da un ricercatore dell'IBM di nome Edward F.Codd come un'idea di modello logico molto semplice e nello stesso tempo in grado di superare i limiti degli altri modelli utilizzati precedentemente, ovvero il modello gerarchico e quello reticolare. Inoltre, il modello relazionale, a differenza degli altri due, definiti tramite un processo di astrazione da sistemi già implementati, è stato definito a livello teorico prima di qualsiasi implementazione sul computer.
Si tratta di un'organizzazione integrata di dati che si basa su alcuni concetti tipicamente matematici e ,soprattutto, assegna grande importanza all'uso rigoroso del linguaggio matematico eliminando in questo modo problemi di ambiguità nella terminologia e nella simbologia, e fornendo d'altra parte, un apparato teorico per dimostrarne tutte le proprietà e le caratteristiche di questo modello.
Il concetto matematico che sta alla base dei database relazionali è quello di relazione della teoria degli insiemi. Un insieme è una "collezione" di dati che possono essere indicati come segue:
A = B =
Per potere definire una relazione occorre prima definire un'operazione tra gli insiemi A e B : ovvero il prodotto cartesiano che darà luogo all'insieme di tutte le possibili coppie di valori appartenenti agli insiemi A e B.
A x B =
Questa operazione può essere estesa a più di due insiemi, definendo quindi il prodotto cartesiano tra n insiemi. In questo caso il risultato sarà un insieme di n-uple anziché un insieme di coppie di valori.
Ora, una relazione è il sottoinsieme dell'insieme di tutte le n-uple che si ottengono tramite la determinazione del prodotto cartesiano degli insiemi di partenza, detti domini.
Per esempio:
Rel_1 =
Giunti a questo punto si può percepire con facilità che, in un database, la relazione viene comunemente rappresentata con una tabella, avente tante colonne quanti sono i domini, e tante righe quante sono le n-uple.
Il database relazionale è più intuitivo ed espressivo rispetto ai modelli gerarchico e reticolare, la teoria su cui si basa consente di sviluppare definizioni, teoremi e dimostrazioni. Dal punto di vista informatico presenta una semplicità nell'uso e nell'implementazione, e il ritrovamento dei dati viene realizzato operando sulle righe e sulle colonne con gli operatori di selezione, proiezione e congiunzione. Non è necessario, quindi, specificare la sequenza del percorso che deve essere seguito per l'accesso ai dati contenuti nel database come avviene invece negli altri modelli, condizionati dal tipo di cammino insito nella struttura dei dati.
Un altro ambito di interazione tra la matematica e l'informatica è rappresentato dalla crittografia. Ai giorni nostri, la protezione della segretezza digitale è diventata una delle sfide più grandi che si trovano a dover affrontare quei paesi che stanno investendo nella comunicazione a distanza. La crittografia permette di codificare un messaggio, affinché solo il destinatario sia in grado di leggerlo e sicuro che non sia stato alterato da altri. Quando un messaggio viene cifrato (o crittografato) significa che le informazioni vengono per così dire codificate, in modo che possano essere lette solo dal destinatario che conosce la chiave di lettura. È in questo modo che oggi la crittografia fornisce servizi come la firma elettronica e la certificazione del mittente.
La crittografia è un'idea antica, la stessa parola è di derivazione greca: criptòs = nascosto + grafia = scrittura, ma prima dell'avvento dell'era del network e degli scambi delle informazioni a distanza sfruttando le tecnologie delle reti, la crittografia era impiegata esclusivamente dai servizi segreti e dall'esercito degli stati.
Questa tecnica ha subito una serie di evoluzioni nella storia; lo sviluppo della crittografia può essere considerato come una lotta alla sopravvivenza in quanto una volta un codice viene decrittato, esso perde utilità diventando incapace di assolvere al suo ruolo. Questo sviluppo ha portato alla nascita della crittografia asimmetrica in cui la chiave usata per cifrare e quella usata per decifrare non coincidono, e questo significa che chi ha cifrato un messaggio non è detto che sia in grado di decifrarlo, lo sarà solo nel caso in cui conosca la chiave per decifrarlo. In questo modo, nell'ipotesi che la cifratura asimmetrica sia una forma di crittografia computerizzata, la chiave per cifrare il messaggio da parte del mittente sarà un numero (detto chiave pubblica in quanto viene usata da tutti i mittenti), e quella per decifrarlo in possesso del destinatario solamente (detta chiave privata) sarà un altro numero. Così se Bob vuole mandare un messaggio ad Alice, è sufficiente che impieghi la chiave pubblica, che potrebbe cercare in una sorta di elenco telefonico.
Il messaggio crittato è inviato ad Alice, che lo decifra con la chiave privata. In modo analogo Carlo,Davide ed Enrico possono inviare ad Alice messaggi crittati con la sua chiave pubblica, mentre solo Alice dispone della chiave privata necessaria a renderli intelligibili. Il grande pregio di questo sistema è che Bob non deve aspettare di ricevere informazioni da Alice per cifrare il messaggio a lei destinato: poiché la chiave per cifrare è pubblica, gli basta consultare un elenco. Mentre Alice non deve più preoccuparsi di comunicare la chiave per cifrare a Bob in condizioni di sicurezza come avveniva nella crittografia simmetrica, in cui la chiave usata dal mittente per cifrare è la stessa usata dal destinatario per decifrare, in sostanza, mittente e destinatario si trovano a disporre di informazioni equivalenti.
Dal punto di vista matematico, un sistema asimmetrico ha lo stesso comportamento di una funzione unidirezionale; Bob può crittare il messaggio con la chiave di Alice, ma non è in grado di decrittarlo. Alice invece deve possedere le informazioni necessarie per poterlo decrittare, in altre parole deve avere i dati che rendono bidirezionale la funzione. Molti studiosi parteciparono alla ricerca di una funzione con le proprietà necessarie alla crittografia asimmetrica ideata da un matematico statunitense di nome Whitfield Diffid insieme agli informatici Martin Hellman e Ralph Merkle nel 1976.
La realizzazione pratica dell'idea della crittografia a chiave pubblica fu raggiunta nell'aprile del 1977 da un trio di ricercatori al MIT (Massachusetts Institute of Technology), composto da Ronald Rivest, Adi Shamir e Leonard Adleman -anche se fu Rivest a scoprire la funzione matematica adatta- che formularono la cifratura RSA.
Una funzione unidirezionale F è una funzione biunivoca che si calcola "facilmente", mentre è praticamente impossibile calcolare la sua inversa. Il calcolo dell'inversa di F è "semplice" se si conosce un'opportuna informazione: la chiave privata.
Il sistema RSA è una cifratura a chiave pubblica e sfrutta le proprietà dei numeri primi.
Non discuterò in modo dettagliato la funzione unidirezionale di Rivest, ma ne spiegherò un aspetto particolare, noto semplicemente come N.
Il numero N è importante perché è la componente flessibile della funzione unidirezionale; ciò significa che ognuno può scegliere un valore N, e personalizzare la funzione.
Per stabilire il valore personale di N, il destinatario (Alice) sceglie due numeri primi p e q, e li moltiplica. Così N è dato da p x q, e costituisce la chiave pubblica accessibile da tutti. Quando un mittente (Bob) vuole mandare un messaggio crittato ad Alice, dovrà innanzitutto procurarsi il valore di N , e inserirlo nella formula generale della funzione unidirezionale, anch'essa di pubblico dominio. A questo punto Bob dispone di una funzione unidirezionale personalizzata tramite la chiave pubblica di Alice, per cifrare il messaggio egli lo introduce nella funzione, prende nota del risultato e lo invia alla destinataria.
A questo punto il messaggio crittato è sicuro; solo una persona può decifrarlo. Poiché la cifratura è il risultato di una funzione unidirezionale, volgerla in chiaro è molto difficile, Alice ci riesce perché, in realtà, pur avendo reso pubblico il valore di N, non ha rivelato i valori di p e q; perciò solo lei dispone delle informazioni extra necessari per la decifrazione.
Possiamo pensare a N come la chiave pubblica, e a p e q come alla chiave privata.
Conoscendo N non è facile ricavare p e q, si tratta di un procedimento molto laborioso, ovvero della scomposizione in fattori primi che richiede molto tempo, e in presenza di numeri eccessivamente grandi (N ha più di cento cifre) diventa sostanzialmente impossibile ricavare p e q.
Tuttavia nessuno ha mai dimostrato che non esista un algoritmo matematico che possa far sì che numeri molto grandi vengano scomposti rapidamente adoperando un computer.
Bibliografia e linkografia:
Saggio di Ennio De Giorgio "Rapporti tra la matematica ed altre forme del sapere umano"
Saggio di Giorgio Lunghini: Forma matematica e contenuto economico
Intervento
del prof. Achille Basile al convegno "Matematica e Cultura
"Introduzione alla teoria del comportamento del consumatore" di Pier Mario Pacini
Microeconomia di Andrew Schotter
"Codici & Segreti" di Simon Singh
'Il teorema del pappagallo' di Guedj Denis
https://matematica.unibocconi.it/
 |
| Appunti su: calcolare punto non accessibile direttamente in un trisavolo triangolo, |
|
| Appunti Geografia |  |
| Tesine Contabilita |  |
| Lezioni Fisica |  |