 |
|
| Appunti scientifiche |
|
|
|
| Appunti scientifiche |
|
| Visite: 1817 | Gradito: |   [ Picolo appunti ] |
Leggi anche appunti:GeometriaGEOMETRIA DEFINIZIONE GEOMETRICA Ripartizione di un segmento in due Una verità millenaria : "Gli Elementi" di Euclide e i postulati della geometriaUna verità millenaria : "Gli Elementi" di Euclide e i postulati della geometria Il La matematica e il linguaggio: il problema della completezzaLa matematica e il linguaggio: il problema della completezza |
 |
 |
L'equazione della retta
Anche in questo caso si tralascerà la parte più teorica (che presuppone una capacità d'astrazione più elevata) per spiegare la parte più operativa.
L'equazione delle retta in forma implicita ha questa forma :
La lettera a è chiamata coefficiente della x, la lettera b coefficiente della y e la lettera c termine noto. Esse non sono altro che dei numeri. Ad esempi se a=2, b=3 e c=5 la retta avrà questa equazione:
.
Partendo dalla forma implicita isoliamo la y a sinistra del segno =, portando tutto il resto a sinistra:
quindi dividendo
tutto per 3 (il coefficiente della y,
cioè la b)
semplificando
otteniamo 
che è detta forma esplicita.
La
forma esplicita letterale è 
Compiamo
un ulteriore passo. Se poniamo 
l'equazione nella sua
forma finale diventa
Il coefficente angolare
Proviamo a disegnare una retta su un piano cartesiano, sapendo che essa passa per i punti A(3;2) e B(6;6) (per disegnare una retta è sufficiente conoscere due punti per cui passa).
Fig. 6
Vediamo che essa
forma un angolo con l'asse delle X. Se la retta passa forzatamente per A e B
l'angolo formato potrà essere solo quello. L'angolazione della retta è misurata
dal coefficiente angolare, che
nell'equazione è rappresentato da 
, ossia da 
. Maggiore è il valore di m, maggiore sarà l'inclinazione della retta. Conoscendo l'equazione
della retta possiamo ricavare il coefficiente angolare. Inoltre valori negativi
di m, significano che la retta
forma un angolo ottuso con l'asse delle X. Gli esempi in figura 7 chiariscono
quanto detto.
Fig. 7
Disegnare la retta
Conoscendo l'equazione della retta calcoliamo almeno due punti per disegnarla.
Se l'equazione è 
attribuiamo una valore
a piacere alla x sostituiamolo
nell'equazione e calcoliamo la y
Se la x
, la y sarà uguale a A(0;3)
Se la x=
allora la y sarà
uguale a B(1;5)
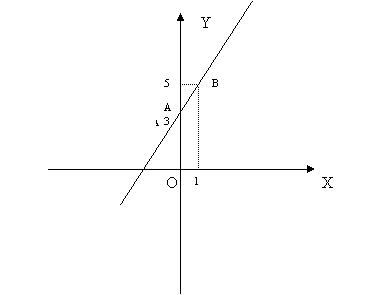
Equazione della retta passante per due punti
Siano dati i punti A(3;2) e B(6;6). Per trovare l'equazione della retta passante per questi due punti si usa la seguente formula:
Retta passante per 2 punti
rappresenta l'ordinata del punto B, cioè 6; 
rappresenta l'ordinata del punto A, cioè 2; 
rappresenta l'ascissa del punto B, cioè 6; 
rappresenta l'ascissa del punto A, cioè 3; 
ed 
sono elementi
letterali che si scrivono senza essere sostituiti da un numero. Svolgiamo i
calcoli
Calcolando il minimo comune multiplo e svolgendo abbiamo
svolgiamo i calcoli
ossia 
che rappresenta
l'equazione della retta in forma implicita.
Equazione della retta di coefficiente angolare noto e passante per un punto
Si
calcoli l'equazione della retta avente coefficiente angolare 
e passante per il
punto A(3;5)
La formula da usare è la seguente
Retta passante per un punto e di coefficiente
angolare noto
Usiamo i valori del punto e del coefficiente angolare con la formula data
Condizione di parallelismo e di perpendicolarità tra due rette
Tralasciando la parte teorica riguardante i fasci di rette per i motivi già detti si enunciano solo le due condizioni:
parallelismo: due rette sono parallele se i loro coefficienti angolari sono uguali
m
es.: 1)
2) 
3) 
perpendicolarità: due rette sono perpendicolari fra loro se i rispettivi coefficienti angolari sono opposti ed inversi.
La 1) e la 2) sono perpendicolari perché
nella prima
e nella seconda 
(opposto di segno e inverso in quanto "capovolto")
Es: 1) 
2) 
3) 
Distanza di un punto da una retta
Siano dati il punto
A(3;-1) e la retta 
.
La formula per calcolare la distanza è la seguente:
distanza di un punto da una retta
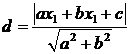
Il denominatore va preso in valore assoluto, cioè privo di segno. Calcolando:
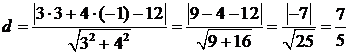
Rette particolari
Esistono alcune rette particolari di cui è importante conoscere le equazioni.
Asse delle ascisse: essendo sul piano è anch'esso una retta, con la particolarità che
tutti suoi punti hanno ordinata uguale a zero, per cui la sua equazione è 
Asse delle ordinate: analogamente l'asse delle ordinate ha equazione 
Bisettrice del 1° e 3°
quadrante: su questa retta, che divide in modo
simmetrico sia il primo che il terzo quadrante, ogni ascissa ha valore uguale
all'ordinata, per cui l'equazione è 
Bisettrice del 2° e4°
quadrante: In questo caso ogni ascissa ha valore
opposto a quello dell'ordinata (stesso numero, ma segno opposto) per cui
l'equazione è 
Intersezione fra due rette
Date due rette su un piano cartesiano, a meno che le due rette non siano parallele, sicuramente si intersecheranno in un punto. Per trovare le coordinate di questo punto è sufficiente mettere a sistema le due equazioni (per informazioni più dettagliate sulla risoluzione dei sistemi di primo grado si veda uno dei moduli precedenti). La x e la e la y trovate sono l'ascissa e l'ordinata del punto.
Es.
e 
Ricaviamo la y dalla prima
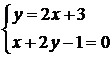
P
per sostituzione
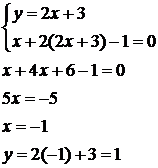
P(-1;1)
|
| Appunti su: retta passante per 3 quadranti3F, riassunti della definizione di retta, |
|
| Appunti Geografia |  |
| Tesine Fisica |  |
| Lezioni Contabilita |  |