 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1989 | Gradito: |
Leggi anche appunti:L'eredità dell'OttocentoL'eredità dell'Ottocento Par. 1) Sviluppi dell'analisi Nel XIX secolo Fondamentali e definizione di campo vettoriale (I)Fondamentali e definizione di campo vettoriale (I) L'inizio più logico coincide Teoremi di rolle e di lagrangeTEOREMI DI ROLLE E DI LAGRANGE I due teoremi che ci accingiamo a |
 |
 |
La vita è limitata...il limite finito
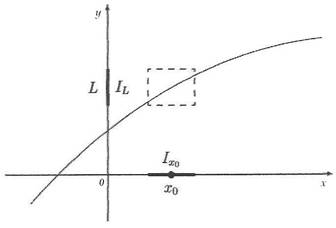 Il concetto limite
in matematica è proprio del calcolo infinitesimale, e permette di
esprimere il comportamento di una funzione quando la sua variabile indipendente
x tende indefinitamente a un valore prefissato. Il concetto, formalizzato in
modo rigoroso nel XIX secolo da Cauchy e Weierstrass, era già comparso in forma
embrionale nella matematica greca e, successivamente, negli scritti di Eulero.
Il concetto limite
in matematica è proprio del calcolo infinitesimale, e permette di
esprimere il comportamento di una funzione quando la sua variabile indipendente
x tende indefinitamente a un valore prefissato. Il concetto, formalizzato in
modo rigoroso nel XIX secolo da Cauchy e Weierstrass, era già comparso in forma
embrionale nella matematica greca e, successivamente, negli scritti di Eulero.
![]()
![]()
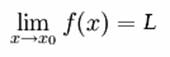
Definizione
Data una funzione reale di variabile reale y = f(x), il valore L è il limite di f(x) per x che tende a x0, se vale la seguente proprietà: presa una qualunque quantità positiva, esiste δ (una quantità dipendente da ), tale che per tutti i valori di x che soddisfano la relazione |x - x0| minore di δ, vale la disuguaglianza: |f(x)-L| <
Se una funzione è continua in un suo punto, il limite per x che tende a x0 coincide con il valore f(x0) che la funzione assume in quel punto cioè y = f(x) continua in x0 quando limite di f(x) per x che tende a x0 è uguale a f(x0). Se invece la funzione non è continua nel punto x0, a seconda della natura della discontinuità il limite per x che tende a x0 può assumere un valore finito diverso da f(x0), oppure può tendere all'infinito.
In particolare
I punti in cui una funzione non è continua si dicono punti di discontinuità. Si dice punto di discontinuità di una funzione reale di variabile reale f un punto appartenente al dominio di definizione di f ma in cui f non è continua.
Comunemente, viene considerato punto di discontinuità anche un punto che non appartiene al dominio di f, ma appartiene alla parte interna della chiusura di f (in pratica un punto per cui abbia senso definire un limite destro e un limite sinistro di f). In particolare, presa una funzione f(x) definita in un intervallo [a,b] (tranne al più in x0) e considerando un punto x0 appartenente allo stesso intervallo, la funzione presenterà in quel punto:
![]() una discontinuità di
prima specie (o punto singolare) se il valore del limite destro, per x tendente a x0,
è diverso dal valore del limite sinistro (graficamente la funzione
presenterebbe un salto);
una discontinuità di
prima specie (o punto singolare) se il valore del limite destro, per x tendente a x0,
è diverso dal valore del limite sinistro (graficamente la funzione
presenterebbe un salto);
![]() una discontinuità di
seconda specie se almeno uno dei due limiti, per x tendente a x0, è
infinito (sia positivo che negativo) oppure non esiste;
una discontinuità di
seconda specie se almeno uno dei due limiti, per x tendente a x0, è
infinito (sia positivo che negativo) oppure non esiste;
![]() una discontinuità di
terza specie (o discontinuità eliminabile) se esistono uguali e finiti i limiti
destro e sinistro, per x tendente a x0, ma il loro valore è diverso
da f(x0) o x0 non è nel dominio della funzione.
una discontinuità di
terza specie (o discontinuità eliminabile) se esistono uguali e finiti i limiti
destro e sinistro, per x tendente a x0, ma il loro valore è diverso
da f(x0) o x0 non è nel dominio della funzione.
 Discontinuità di prima specie
(o di salto)
Discontinuità di prima specie
(o di salto)
![]() Un punto x0
si dice di discontinuità di prima specie quando il limite destro della funzione, per x che
tende a x0, è diverso da quello sinistro, pur essendo entrambi
valori finiti. Ovvero:
Un punto x0
si dice di discontinuità di prima specie quando il limite destro della funzione, per x che
tende a x0, è diverso da quello sinistro, pur essendo entrambi
valori finiti. Ovvero:
![]()
La discontinuità
viene comunemente definita "di salto" perché l'aspetto del grafico è quello di
un salto nel punto di discontinuità. Un tipico esempio si ha nel caso della
funzione ![]() definita per
definita per ![]() che vale sempre 1 per x positivi e -1 per x
negativi e fa un "salto" in x = 0.
che vale sempre 1 per x positivi e -1 per x
negativi e fa un "salto" in x = 0.
 Discontinuità di seconda specie (o
essenziale)
Discontinuità di seconda specie (o
essenziale)
Un punto x0 si dice di discontinuità di seconda specie quando il limite della funzione per x che tende a x0 da destra e/o da sinistra, tende ad infinito o non esiste affatto. Quindi
![]()
![]() oppure
oppure
![]() quindi
quindi
![]()
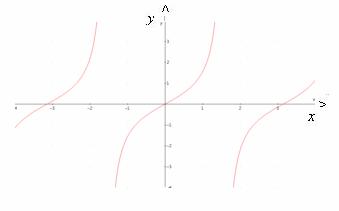
Un esempio con il
limite infinito può essere la funzione che vale ![]() per
per ![]() o dalla funzione tangente.
Un esempio in cui il limite non esiste è dato dalla funzione
o dalla funzione tangente.
Un esempio in cui il limite non esiste è dato dalla funzione ![]() per
per ![]() .
.
 Discontinuità
di terza specie (o eliminabile)
Discontinuità
di terza specie (o eliminabile) Un punto x0
si dice di discontinuità di terza specie quando il limite destro della funzione,
per x che tende a x0, è uguale a quello sinistro, con entrambi
valori finiti, ma diversi dall'eventuale valore di f in x0. Ovvero,
se ![]() :
:
![]()
![]()
La discontinuità viene comunemente definita "eliminabile" in quanto è sufficiente modificare opportunamente il valore da assegnare alla funzione nel punto di discontinuità per renderla continua in quel punto oppure, nel caso che x0 non sia nel dominio, estendere la funzione assegnandogli in x0 il valore del limite.
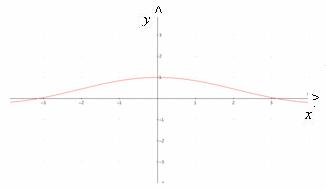
Un tipico esempio è dato
dalla funzione ![]() che
a priori è definita solo per
che
a priori è definita solo per ![]() ma si può estendere ad una funzione continua
in 0 ponendo f(0) uguale al suo limite in 0, cioè 1.
ma si può estendere ad una funzione continua
in 0 ponendo f(0) uguale al suo limite in 0, cioè 1.
 |
| Appunti su: vite al limite angel come C3A8 finita, |
|
| Appunti Contabilita |  |
| Tesine Fisica |  |
| Lezioni Statistica |  |