 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1611 | Gradito: |
Leggi anche appunti:Risoluzione di una equazione differenziale del secondo ordineRISOLUZIONE DI UNA EQUAZIONE DIFFERENZIALE DEL SECONDO ORDINE TIPI DI EQUAZIONI Angolo di incidenza di due retteAngolo di incidenza di due rette Siano due rette di equazione r: GeometriaGEOMETRIA DEFINIZIONE GEOMETRICA Ripartizione di un segmento in due |
 |
 |
TEOREMI DI ROLLE E DI LAGRANGE
I due teoremi che ci accingiamo a dimostrare sono detti teoremi fondamentali del calcolo con le derivate.
TEOREMA DI ROLLE
Sia f(x)
una funzione continua nell'intervallo compatto [a, b], derivabile nei punti
interni ad [a, b]. se f(a)=f(b) esiste un punto ![]() interno ad [a, b] tale
che
interno ad [a, b] tale
che ![]() . In altri termini vale la seguente implicazione:
. In altri termini vale la seguente implicazione:
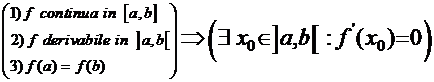
Dim
Per il teorema di Weistrass che vale in virtù
dell'ipotesi 1) f(x) ha in [a, b] minimo e massimo. Ciò significa che ![]()
![]()
Se ![]() è evidente che la
funzione f è costante in [a, b] e il teorema di Rolle è certamente vero quindi
si ricordi che la derivata di una costante è nulla.
è evidente che la
funzione f è costante in [a, b] e il teorema di Rolle è certamente vero quindi
si ricordi che la derivata di una costante è nulla.
Se per
l'ipotesi 3) almeno uno dei due punti ![]() . Se per esempio
. Se per esempio ![]() è interno ad [a, b] allora
è interno ad [a, b] allora ![]() essendo un punto di
estremo assoluto, è anche un punto di estremo relativo nel quale f è derivabile
per l'ipotesi 2). Dal teorema di Fermat
si deduce che
essendo un punto di
estremo assoluto, è anche un punto di estremo relativo nel quale f è derivabile
per l'ipotesi 2). Dal teorema di Fermat
si deduce che![]() e il teorema di Rolle è completamente dimostrato.
e il teorema di Rolle è completamente dimostrato.
Osservazione 1
Se consideriamo il diagramma di una funzione f che verifica l'ipotesi del teorema di Rolle allora questo teorema afferma che esiste almeno un punto c del diagramma, distinto dagli estremi a e b, in cui la tangente geometrica è parallela all'asse x.
Osservazione 2
La continuità di f(x) negli estremi dell'intervallo [a,b] è indispensabile.
Consideriamo ad esempio la funzione 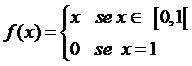
 Tale funzione è derivabile in
Tale funzione è derivabile in![]() ma non è continua in [0, 1] perché nel punto
ma non è continua in [0, 1] perché nel punto ![]() . inoltre vale (per
l'ipotesi 2) f(0)=f(1)=0 . Ebbene,
essendo
. inoltre vale (per
l'ipotesi 2) f(0)=f(1)=0 . Ebbene,
essendo ![]() tale funzione non verifica la tesi del teorema di Rolle.
tale funzione non verifica la tesi del teorema di Rolle.
TEOREMA DI LAGRANGE
Se f(x) è una funzione continua
nell'intervallo compatto [a,b] e derivabile nei punti interni ad [a,b], esiste
un punto![]() interno ad [a,b] tale che:
interno ad [a,b] tale che:
![]()
Questa uguaglianza si chiama formula di Lagrange.
Dim
Consideriamo la funzione ausiliare
![]()
La quale,geometricamente, rappresenta la differenza tra le ordinate del punto P del diagramma e del punto Q della retta congiungente gli estremi A=(a,f(a)), B=(b,f(b)) aventi la stessa ascissa(distanza variabile del diagramma della retta).
Si verifica facilmente che g(a)=g(b)=0. D'altra parte g è continua
in [a,b], derivabile in![]() risulta
risulta
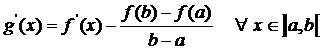
Ne segue, per il teorema di Rolle, che esiste
un punto ![]()
![]() . Ma ciò equivale a dire che esiste un punto
. Ma ciò equivale a dire che esiste un punto![]()
![]() .
.
Il teorema è dimostrato.
 |
| Appunti su: teorema di lagrange appunti, |
|
| Appunti Fisica |  |
| Tesine Contabilita |  |
| Lezioni Geografia |  |