 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3243 | Gradito: |
Leggi anche appunti:Proprietà delle serie convergentiProprietà delle serie convergenti Le serie convergenti godono di alcune proprietà Un nuovo postulato delle paralleleUN NUOVO POSTULATO delle parallele Una trentina d'anni dopo la pubblicazione La matematica oltre il numeroLa matematica oltre il numero La matematica, considerata nel modo giusto, |
 |
 |
I Pitagorici e la Prima Teoria del Suono
"Musica è un esercizio aritmetico della mente
che conta senza sapere di contare"
Gottfried Leibniz
Pitagora di Samo (575ca. -490ca. a.C.) filosofo greco, che coniò la parola kósmos per indicare la bellezza, l'armonia, la simmetria dell'universo, fu il primo occidentale a compiere studi sperimentali sulla natura del suono; a lui è attribuito il merito di aver scoperto che gli intervalli musicali possono esser regolamentati da definiti rapporti di numeri interi.
![]()
I pitagorici riuscirono a definire i rapporti numerici esistenti tra i vari suoni attraverso l'uso di uno strumento sperimentale esistente all'epoca: il monocordo.
 Il monocordo consisteva in una sola corda di budello o di metallo tesa
fra 2 ponti appoggiati su di una cassa di risonanza ed era dotato di un
ponticello mobile che poteva scorrere liberamente da un ponte all'altro creando
un terzo punto fisso. Grazie a quest'ultimo la corda veniva suddivisa in due
parti le cui lunghezze erano variabili a piacere permettendo l'esecuzione di
accordi formate da coppie di suoni con altezze aventi tra loro un rapporto
definibile.
Il monocordo consisteva in una sola corda di budello o di metallo tesa
fra 2 ponti appoggiati su di una cassa di risonanza ed era dotato di un
ponticello mobile che poteva scorrere liberamente da un ponte all'altro creando
un terzo punto fisso. Grazie a quest'ultimo la corda veniva suddivisa in due
parti le cui lunghezze erano variabili a piacere permettendo l'esecuzione di
accordi formate da coppie di suoni con altezze aventi tra loro un rapporto
definibile.
I pitagorici giunsero a due principali scoperte:
 L'altezza del suono è inversamente proporzionale alla lunghezza
della corda vibrante.
L'altezza del suono è inversamente proporzionale alla lunghezza
della corda vibrante. Attraverso il monocordo, i pitagorici si concentrarono sull'enunciare una definizione matematica di suono gradevole, detto anche consonanza: due o più suoni simultanei (un accordo) sono considerati gradevoli nel caso in cui il rapporto fra le due altezze è definito da piccoli numeri (3:2 , 4:3 , ecc).
 Sul monocordo questo rapporto
corrisponde alle lunghezze delle parti della corda. Per esempio si chiama intervallo
(o accordo) di quinta, la combinazione di due suoni emessi da una corda intera
e da una corda in cui il ponticello mobile è stato fissato a una distanza di 2/3
dal piolo. Se L è la lunghezza della
corda e il piolo è fissato a 2/3 L allora L: 2/3L= 3: 2.
Sul monocordo questo rapporto
corrisponde alle lunghezze delle parti della corda. Per esempio si chiama intervallo
(o accordo) di quinta, la combinazione di due suoni emessi da una corda intera
e da una corda in cui il ponticello mobile è stato fissato a una distanza di 2/3
dal piolo. Se L è la lunghezza della
corda e il piolo è fissato a 2/3 L allora L: 2/3L= 3: 2.
Similmente un intervallo (o accordo) di ottava corrisponde a una combinazione di suoni ottenuti da due corde di cui una è la metà dell'altra. Se L è la lunghezza della corda e il piolo è fissato a 1/2 L allora L: 1/2L= 1: ½= 2:1.
Nella cultura occidentale, l'ottava si chiama così perchè contiene 8 note (se si contano anche gli estremi della corda). I pitagorici chiamavano l'accordo di ottava "diaposon" (in greco "attraverso tutte le note"). È curioso notare che quasi tutte le culture basano le proprie scale sull'intervallo di ottava, anche se per esempio nella cultura indiana l'ottava si divide in 22 parti, nella cultura cinese in 5 parti e in quella arba in 17 parti.
Infine la quarta perfetta corrisponde a una combinazione di due suoni emessi da una corda intera e da una corda in cui il ponticello mobile è stato fissato a una distanza di 3/4 dal piolo. Se L è la lunghezza della corda e il piolo è fissato a 3/4 L allora L: 3/4L= 4: 3.
La scala è una sequenza di note in ordine ascendente o discendente collocate secondo criteri che tengono presente le consonanze degli intervalli.
La scala pitagorica
La scala pitagorica è una sequenza di 7 note costruita con una progressione di intervalli di quinta. La denominazione di ogni nota e l'uso pratico delle note famose DO RE MI FA SOL LA SI è una procedura alquanto convenzionale che assegna un nome per un preciso intervallo di quinta.
Questi nomi "convenzionali" sono da attribuire a Guido d'Arezzo (991- ),monaco e musicologo italiano, il quale ha voluto facilitare i musicisti utilizzando le sillabe iniziali dei versi dell'inno a San Giovanni Battista di Paolo Diacono per comporre la scala musicale (scelta dovuta al fatto che ogni verso dell'inno inizia con un tono più alto rispetto al precedente)
Inno a San Giovanni
Ut queant laxis
Resonare fibris
Mira gestorum
Famuli tuorum
Solve polluti
Labii reatum
Sancte Iohannes
('affinché i tuoi servi possano cantare con voci libere le meraviglie delle tue azioni, cancella il peccato del loro labbro contaminato, o san Giovanni').
La scala pitagorica è costruita a partire dai rapporti numerici di cui sopra: 1:1, 2:1, 3:2, 4:3 alzando o abbassando al nota di riferimento per una quinta. La scala pitagorica è la seguente:
RE MI FA SOL LA SI DO RE'
9/8 32/27 4/3 3/2 27/16 16/9 2/1
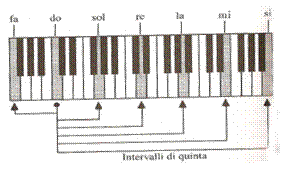 È interessante notare che, malgrado la riconosciuta consonanza delle
terze e delle seste, la scala pitagorica fu costruita escludendo questi
rapporti di intervallo e basandosi soltanto sull'ottava e sulla quinta. Ciò
perchè i numeri 5,6 e 8 non fanno parte dalla quaterna, che va da 1 a 4, ossia
quella dei numeri che, sommati, danno 10, il numero perfetto per i pitagorici.
È interessante notare che, malgrado la riconosciuta consonanza delle
terze e delle seste, la scala pitagorica fu costruita escludendo questi
rapporti di intervallo e basandosi soltanto sull'ottava e sulla quinta. Ciò
perchè i numeri 5,6 e 8 non fanno parte dalla quaterna, che va da 1 a 4, ossia
quella dei numeri che, sommati, danno 10, il numero perfetto per i pitagorici.
In linea teorica in un'ottava sono contenute infinite frequenze ed è opera dell'uomo la suddivisione di questa in un certo numero di gradi discreti. Merito appunto dei pitagorici la creazione di una scala ottenuta per esclusivi salti di quinta perfetta (in figura).
La scala pitagorica sopravvisse fino all'introduzione del canto polifonico nel Medioevo. Gli schemi pitagorici furono usati nella musica liturgica e il canto gregoriano ne è la testimonianza più conosciuta.
Consonanza e Dissonanza
![]()


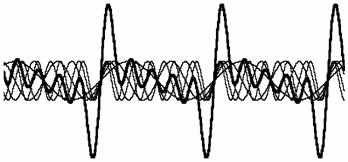
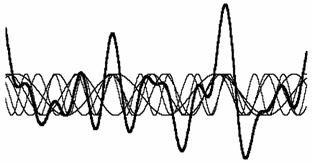
Suoni consonanti Suoni dissonanti
 Nel
grafico le linee sottili rappresentano le singole armoniche mentre la
linea spessa rappresenta l'accordo. Come si può notare dalle figure
sovrastanti di sinistra nell'intervallo do-sol
(V) sono numerosi i punti X0 in cui entrambe le curve meno spesse
intercettano l'asse orizzonatle (nel caso specifico tutti i multipli di 3) dando
origine a una curva da una forma d'onda regolare. Il rapporto tra i due
suoni infatti è di 3:2, e se suonati insieme daranno un suono complessivo molto
piacevole, di qui infatti la denominazione della quinta come accordo
perfetto. Al contrario l'intervallo do-si
(VII) si trova in un rapporto 15:8, di conseguenza risulterà assai
sgradevole poichè non vi sono punti X0 frequenti e la forma
della linea piu' spessa è alquanto irregolare.
Nel
grafico le linee sottili rappresentano le singole armoniche mentre la
linea spessa rappresenta l'accordo. Come si può notare dalle figure
sovrastanti di sinistra nell'intervallo do-sol
(V) sono numerosi i punti X0 in cui entrambe le curve meno spesse
intercettano l'asse orizzonatle (nel caso specifico tutti i multipli di 3) dando
origine a una curva da una forma d'onda regolare. Il rapporto tra i due
suoni infatti è di 3:2, e se suonati insieme daranno un suono complessivo molto
piacevole, di qui infatti la denominazione della quinta come accordo
perfetto. Al contrario l'intervallo do-si
(VII) si trova in un rapporto 15:8, di conseguenza risulterà assai
sgradevole poichè non vi sono punti X0 frequenti e la forma
della linea piu' spessa è alquanto irregolare.
Ma perchè si può definire un accordo piacevele e dolce e un altro accordo invece ci puo' risultare aspro all'orecchio? E qual'è la differenza tra suono e rumore (comunemente identificato come una sensazione uditiva sgradevole e fastidiosa o intollerabile).
La psicoacustica è la scienza che si occupa di determinare scientificamente le influenze che possono avere determinati suoni sul nostro organismo. Per quanto riguarda la sensazione di piacere che noi abbiamo nell'ascoltare un complesso di suoni emessi in un tempo relativamente breve, questa è dovuta alle caratteristiche fisiche del suono, primo fra tutti la regolarità. I neuroni uditivi periferici cercano, infatti, di codificare simmetrie temporali nella struttura del messaggio acustico; tali regolarità semplificano i meccanismi di elaborazione del cervello e, quanto più sono fitte, tanto più il piacere della consonanza sarà intenso. Inoltre la semplicità del messaggio acustico favorisce non solo la nostra sensazione di piacere, quanto anche l'attenzione e la memoria. Nella figura sono riportate le frequenze ottenute facendo risuonare due note di diversa frequenza contemporaneamente; le rispettive onde si troveranno periodicamente in concordanza (consonanti) o opposizione (dissonanza) di fase (distanza tra due picchi) con frequenza pari alla differenza delle frequenze dei due suoni.
".ciò che si oppone alla nostra apprensione, ossia l'irrazionale o la dissonanza, diventa immagine naturale di ciò che si oppone alla nostra volontà; e viceversa la consonanza, o il razionale, facilmente dominabile dalla nostra facoltà di apprensione, diventa l'immagine di ciò che soddisfa la volontà"
Arthur Schopenauer
L'armonia celeste: dai Pitagorici a Keplero
"L'armonia risiede nel magico potere dei numeri"
Pitagora
Il padre della teoria dell'armonia celeste è Pitagora (575ca.-490ca. a.C.) e la sua scuola pitagorica. Questi furono i primi a dedicarsi in maniera razionale al problema cosmologico; per esempio la definizione di cosmo la dobbiamo a Pitagora, il primo che usò questo termine per indicare l'ordine e l'eleganza dell'universo (kosmos = ordine, armonia universale). I Pitagorici inoltre furono i primi a sostenere che i pianeti avessero una forma sferica e ad ipotizzare un sistema eliocentrico, anche se al centro dell'universo non vi è il Sole ma l'Hestia, il fuoco centrale che fa brillare lo stesso Helios di luce riflessa. La struttura complessiva dell'universo proposta da Pitagora e perfezionata dai suoi seguaci puo' essere riassunta come di seguito (tratto dalla descrizione di Filolao, filosofo greco che visse nel V secolo a.c.):
 Ogni pianeta ruota nella direzione da Occidente a Oriente attorno a un fuoco
centrale.
Ogni pianeta ruota nella direzione da Occidente a Oriente attorno a un fuoco
centrale.
Tutti i corpi celesti ruotando, come sassi che sfrecciano attraverso l'aria, emettono un suono, ciascuno il proprio. Il suono è prodotto per effetto dell'attrito contro il mezzo nel quale i corpi celesti navigano (aria o fuoco)
Il suono ha un'altezza proporzionale alla velocita' del corpo celeste la quale a sua volta È proporzionale all distanza di ogni corpo celeste dal fuoco centrale.
I rapporti tra le altezze dei suoni sono tali da dar origine ad accordi musicali sempre armoniosi.
Nessuno percepisce questa "rumorosa" armonia a causa dell'assuefazione, avendola udita fin dalla nascita.
 Ancora nel Seicento, Giovanni Keplero, astronomo e matematico
tedesco (1571 - 1630), riprendeva l'argomento dell'armonia celeste motivato
dalla concezione di un Dio "geometra", architetto supremo che avrebbe
creato l'universo secondo un perfetto progetto matematico. Non a caso proprio
lui ebbe l' "illuminazione"di porre in proporzione di 3 a 2 le potenze dei semiassi maggiori con quelle
dei periodi di rivoluzione, chiamandola terza sua legge ed inserendola in un
testo non esclusivamente astronomico, ma squisitamente astrologico e
musicale. Keplero, volendo meglio giustificare la retrocessione di Marte,
propone una nuova teoria eliocentrica e formula le sue prime due famose
leggi.
Ancora nel Seicento, Giovanni Keplero, astronomo e matematico
tedesco (1571 - 1630), riprendeva l'argomento dell'armonia celeste motivato
dalla concezione di un Dio "geometra", architetto supremo che avrebbe
creato l'universo secondo un perfetto progetto matematico. Non a caso proprio
lui ebbe l' "illuminazione"di porre in proporzione di 3 a 2 le potenze dei semiassi maggiori con quelle
dei periodi di rivoluzione, chiamandola terza sua legge ed inserendola in un
testo non esclusivamente astronomico, ma squisitamente astrologico e
musicale. Keplero, volendo meglio giustificare la retrocessione di Marte,
propone una nuova teoria eliocentrica e formula le sue prime due famose
leggi.
Prima legge
"I pianeti percorrono orbite ellittiche di cui il Sole occupa uno dei fuochi
Seconda legge:
"Il raggio vettore che unisce il centro del Sole con il centro del pianeta descrive aree uguali in tempi uguali.

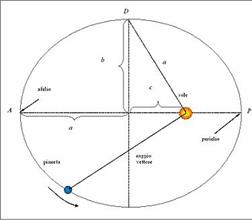
 Quindi la velocità dei pianeti non ha valore costante, e passa invece
attraverso una gamma continua di valori che vanno da un massimo, all'afelio, a
un minimo, al perielio. Rifacendosi alle teorie pitagoriche, risulterebbe che
se i pianeti "suonassero" e si facessero corrispondere dei suono più o meno
acuti a seconda delle loro velocità, allora compiendo una rivoluzione,
genererebbero delle proprie melodie. Trova così delle proporzioni tra le
velocità angolari in afelio e perielio delle varie orbite che per esempio per Saturno
corrisponde a 5/4 (terza maggiore), per Marte circa 3/2 (quinta
perfetta). Per le note intermedie, Keplero in modo totalmente arbitrario,
individua lungo le orbite, un certo numero di posizioni privilegiate per farle
corrispondere a note sul pentagramma. Dalle sei melodie considerate
simultaneamente, trae origine l'armonia universale.
Quindi la velocità dei pianeti non ha valore costante, e passa invece
attraverso una gamma continua di valori che vanno da un massimo, all'afelio, a
un minimo, al perielio. Rifacendosi alle teorie pitagoriche, risulterebbe che
se i pianeti "suonassero" e si facessero corrispondere dei suono più o meno
acuti a seconda delle loro velocità, allora compiendo una rivoluzione,
genererebbero delle proprie melodie. Trova così delle proporzioni tra le
velocità angolari in afelio e perielio delle varie orbite che per esempio per Saturno
corrisponde a 5/4 (terza maggiore), per Marte circa 3/2 (quinta
perfetta). Per le note intermedie, Keplero in modo totalmente arbitrario,
individua lungo le orbite, un certo numero di posizioni privilegiate per farle
corrispondere a note sul pentagramma. Dalle sei melodie considerate
simultaneamente, trae origine l'armonia universale.
![]()
Pur non avendo fondamenti scientifici, questo lavoro di Keplero si presenta come una pittoresca visione del grado di deviazione di ciascuna orbita planetaria dalla circonferenza.
 |
| Appunti su: il monocordo di pitagora, |
|
| Appunti Statistica |  |
| Tesine Geografia |  |
| Lezioni Contabilita |  |