 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2279 | Gradito: |
Leggi anche appunti:Equilibri eterogeneiEquilibri eterogenei Fino ad ora abbiamo trattato soluzioni acquose, che Lo Stato SolidoLo Stato Solido Allo stato solido, le particelle - che possono essere presenti Radiazioni elettromagnetiche e atomiRadiazioni elettromagnetiche e atomi Le radiazioni luminose (sia visibili |
 |
 |
Se si possiedono una serie di misure di concentrazione C a tempi diversi è possibili riportarli in un diagramma come ln(C) in funzione del tempo e come 1/C in funzione del tempo. Quello dei due grafici che si presenta come una retta permette di discriminare il tipo di cinetica e la pendenza della retta ci fornisce il valore della costante cinetica k.
Ovviamente la semplice osservazione dei grafici ci fornisce una risposta di tipo qualitativo e non sempre è possibile distinguere "ad occhio" quale dei due insiemi di punti si allinea meglio su di una retta.
Un approccio più rigoroso e quantitativo prevede il calcolo del coefficiente di determinazione R2 per i due insiemi di dati. Il coefficiente di determinazione (il quadrato del coefficiente di correlazione lineare R) può infatti essere utilizzato come una misura della bontà dell'adattamento dei dati ad una retta (regressione lineare). In altre parole ci dice quale dei due gruppi di dati viene più efficacemente rappresentato da una retta.
R2 può assumere valori compresi tra 0 ed 1. Più il valore di R2 si avvicina all'unità e maggiore è l'allineamento dell'insieme di punti analizzato su di una retta.
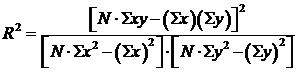
dove
x = variabile indipendente (nel nostro caso il tempo t)
y = variabile dipendente (nel nostro caso ln C o 1/C)
N = numero di dati sperimentali
Sx = Sommatoria di tutti i valori di x
Sy = Sommatoria di tutti i valori di y
Sxy = Sommatoria di tutti i valori dei prodotti xy
Sx2 = Sommatoria di tutti i valori di x2
Sy2 = Sommatoria di tutti i valori di y2
Sx)2 = Quadrato della sommatoria di tutti i valori di x
Sy)2 = Quadrato della sommatoria di tutti i valori di y
Una volta determinato l'insieme di dati che meglio si allinea su di una retta è possibile calcolarne in modo rigoroso la pendenza, e quindi il valore della costante cinetica k, applicando il metodo dei minimi quadrati.

Esempio
Il
saccarosio, in una soluzione acida diluita si idrolizza per dare glucosio e
fruttosio.
I dati sperimentali della velocità della reazione sono raccolti nella seguente
tabella:
|
t (min) |
C = [Saccarosio] mol/L |
Ln C |
1/C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Se ora riportiamo in un grafico la concentrazione in funzione del tempo otteniamo

Se riportiamo in un grafico il logaritmo della concentrazione in funzione del tempo otteniamo

Riportando infine in un grafico il reciproco della concentrazione in funzione del tempo, si ottiene invece

Nel secondo grafico (logaritmo della concentrazione contro tempo) i punti presentano un andamento lineare (si allineano lungo una retta) e dunque l'idrolisi del saccarosio presenta una cinetica del 1° ordine v = k [Saccarosio]
Proviamo ora ad analizzare i dati in modo quantitativo, calcolando il coefficiente di determinazione per ciascuno di essi
|
x |
t (min) |
|
|
|
|
|
Sx = 469 |
|
y |
Conc. |
|
|
|
|
|
Sy = 1,164 |
|
xy |
|
|
|
|
|
|
Sxy = 86,986 |
|
x2 |
|
|
|
|
|
|
Sx2 = 71621 |
|
y2 |
|
|
|
|
|
|
Sy2 = 0,288992 |

|
x |
t (min) |
|
|
|
|
|
Sx = 469 |
|
y |
Ln C |
|
|
|
|
|
Sy = -7,46700048 |
|
xy |
|
|
|
|
|
|
Sxy = -801,90283 |
|
x2 |
|
|
|
|
|
|
Sx2 = 71621 |
|
y2 |
|
|
|
|
|
|
Sy2 = 11,52418586 |

|
x |
t (min) |
|
|
|
|
|
Sx = 469 |
|
y |
1/C |
|
|
|
|
|
Sy = 23,12834563 |
|
xy |
|
|
|
|
|
|
Sxy = 2653,66849 |
|
x2 |
|
|
|
|
|
|
Sx2 = 71621 |
|
y2 |
|
|
|
|
|
|
Sy2 = 115,602325 |
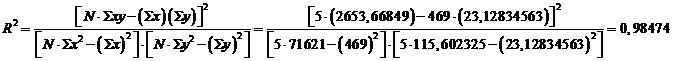
L'analisi quantitativa conferma quanto già evidenziato dall'analisi grafica: il secondo gruppo di dati (ln(C) in funzione del tempo) presenta infatti un coefficiente di determinazione più elevato e dunque la reazione è di primo ordine.
Usando ora i medesimi dati possiamo stimare la costante cinetica k della reazione applicando il metodo dei minimi quadrati che ci permette di calcolare la pendenza della retta ln(C) = ln(C0) kt
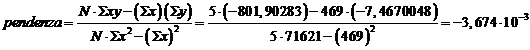
la costante cinetica vale quindi k = 3,674 10-3 min-1
Per una stima più rapida, ma approssimata della costante cinetica è possibile calcolare la pendenza della retta che unisce il punto iniziale (t = 0; C = 0,316) al punto finale (t = 210 ; C = 0,146)
![]()
Suggerimento
Il calcolo del coefficiente di determinazione R2, della pendenza e dell'intercetta possono essere effettuati usando le opportune funzioni di Excel. Nell'immagine successiva, i valori della y sono stati riportati nelle celle A2:A6 ed i valori della x nelle celle B2:B4.

Nella cella D2 si è calcolato il coefficiente di determinazione, usando la funzione CORRELAZIONE(Matrice1;Matrice2) elevata al quadrato (^2). La funzione fornisce infatti il coefficiente di correlazione R. Per il calcolo è necessario sostituire a Matrice1 l'intervallo di celle corrispondenti ai valori della y ed a matrice2 l'intervallo di celle corrispondenti ai valori della x. Nella cella D2 è dunque contenuta la seguente istruzione
=CORRELAZIONE(A2:A6;B2.B6)^2
Nella cella E2 si è calcolato la Pendenza della retta usando la funzione PENDENZA(y_nota;x_nota). Nella cella E2 è dunque contenuta la seguente istruzione
=PENDENZA(A2:A6;B2.B6)
Nella cella F2 si è calcolato l'intercetta della retta con l'asse delle ordinate usando la funzione INTERCETTA(y_nota;x_nota). Nella cella F2 è dunque contenuta la seguente istruzione
=INTERCETTA(A2:A6;B2.B6)
 |
| Appunti su: equazione cinetica integrata, |
|
| Appunti Ingegneria tecnico |  |
| Tesine Biologia |  |
| Lezioni Geografia |  |