 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1981 | Gradito: |
Leggi anche appunti:Caratteristiche chimiche delle acque lacustri alpineCaratteristiche chimiche delle acque lacustri alpine Per quanto riguarda le Uso dell'equazione cinetica integrataUso dell'equazione cinetica integrata Se si possiedono una serie di misure Acidi carbossilici e loro derivatiAcidi carbossilici e loro derivati Gli acidi carbossilici sono composti caratterizzati |
 |
 |
Presentano una cinetica di primo ordine quelle reazioni in cui la velocità è direttamente proporzionale alla concentrazione di un solo reagente, secondo una legge del tipo
![]()
Ciò non significa che nella reazione non possa essere coinvolto più di un reagente, ma solo che la velocità dipende solo da uno dei reagenti presenti.
Nelle reazioni di primo ordine k si esprime in s-1 (infatti si ottiene come v/[A])
Più spesso viene utilizzata l'equazione di velocità integrata (si ottiene integrando la relazione precedente) che mette in funzione la concentrazione con il tempo di reazione t
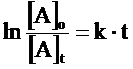
dove
[A]o = concentrazione iniziale di A
[A]t = concentrazione di A al tempo t
k = costante di velocità specifica
t = tempo di reazione
Si noti che, se la reazione segue una cinetica di primo ordine, riportando in un grafico l'andamento del logaritmo della concentrazione in funzione del tempo si ottiene una retta di pendenza -k
![]()

La costante di velocità specifica k può dunque essere calcolata conoscendo le concentrazioni a due tempi diversi. Il rapporto tra la differenza delle ordinate (Δy = ln[A]2 - ln[A]1) e la differenza delle ascisse (Δx = t2 - t1) di due punti fornisce infatti la pendenza della retta.

Esempio 1
Sapendo che la reazione 2N2O5 → 4NO2 + O2 segue una cinetica di primo ordine e che la costante di velocità specifica a 65°C vale k = 5,2.10-3 s-1, calcoliamo la concentrazione di N2O5 dopo 5 minuti, sapendo che la sua concentrazione iniziale era di 0,25 mol/L
![]()
da cui
![]()
Esempio 2
La reazione in fase gassosa A(g) → 2B(g) + C(g) segue una cinetica di primo ordine. In condizioni di volume e temperatura costanti, la pressione totale iniziale del sistema è di 0,2227 atm, mentre dopo 21 minuti la pressione totale è di 0,3744 atm. Calcoliamo la costante di velocità e la pressione totale a 9 minuti.
Al tempo t = 0 la pressione totale è generata solo dal reagente ( i prodotti non si sono ancora formati) per cui la pressione di A al tempo t = 0 è pari a 0.2227 atm.
Al tempo t = 21 min hanno reagito x moli di A per dare 2x moli di B ed x moli di C. Le pressioni parziali dei tre gas avranno subito una variazione proporzionale. Per cui al tempo tempo t = 21 min le pressioni parziali dei tre gas saranno
A(g) → 2B(g) + C(g)
0,2227 - x 2x x
e la pressione totale della miscela al tempo t = 21 min sarà, per la legge di Dalton dell miscele gassose
Pt = PA + PB + PC = (0,2227 -x) + 2x + x = 0,3744 atm
da cui x = 0.07585 atm
La pressione parziale di A al tempo t= 21 min sarà quindi
PA(21 min) = 0,2227 - x = 0,2227 - 0,07585 = 0,14685 atm
Usiamo ora la relazione integrata di velocità per una reazione del primo ordine per calcolare la costante di velocità specifica
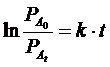
![]()
da cui k = 2 10-2 min-1
Calcoliamo ora la pressione parziale di A al tempo t = 9 min
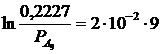
da cui

Se ne deduce che dopo 9 minuti la pressione di A è diminuita di 0.2227 - 0.1860 = 0.0367 atm
Ricordando che per ogni x atmosfere di diminuzione della pressione di A, la pressione di B aumenta di 2x atmosfere e quella di C aumenta di x atmosfere, dopo 9 minuti la pressione parziale dei prodotti sarà
PB = 2(0.0367) = 0.0734 atm
PC = 0.0367 atm
La pressione totale dopo 9 minuti sarà pertanto
Ptot = PA+ PB + PC = 0.1860 + 0.0734 + 0.0367 = 0.2961 atm
Esempio 3
Una reazione del primo ordine presenta una velocità iniziale V0 = 10-2 mol L-1 ore-1. Dopo 40 minuti la velocità si è ridotta ad un decimo. Calcolare la costante di velocità e la concentrazione iniziale del reagente.
Poiché in una reazione di primo ordine la velocità è direttamente proporzionale alla concentrazione del reagente V = k [A], possiamo scrivere
V0 = k [A]0 e Vt = k [A]t
Dividendo membro a membro si ottiene
V0/ Vt = [A]0 /[A]t
e poiché la velocità iniziale V0 è 10 volte maggiore della velocità Vt al tempo t = 40 minuti (4/6 di ora) potremo scrivere
V0/ Vt = [A]0 /[A]t = 10
Scriviamo ora la relazione di velocità integrata per le reazioni di primo ordine
![]()
e sostituiamo
ln (10) = k (4/6)
da cui k = 3,45 ore-1
Usiamo ora la costante di velocità specifica per calcolare la concentrazione iniziale
V0 = k [A]0
e, sostituendo
10-2 = 3,45 [A]0
da cui
[A]0 = 10-2 / 3,45 = 2,90 10-3 mol/L
* * * * * * * *
Seguono cinetiche di primo ordine anche i decadimenti radioattivi, per i quali si calcola generalmente il tempo di dimezzamento

Come si può osservare, nel caso di cinetiche di primo ordine, il tempo di dimezzamento dipende solo dal valore di k e non dalla concentrazione iniziale. Nel caso dei decadimenti radioattivi k prende il nome di costante di decadimento radioattivo. Sapendo ad esempio che la costante di decadimento del carbonio14 è pari a 1,21.10-4 anni-1, possiamo facilmente calcolare il suo tempo di dimezzamento
![]()
 |
| Appunti su: |
|
| Appunti Ingegneria tecnico |  |
| Tesine Geografia |  |
| Lezioni Biologia |  |