 |
|
| Appunti tecniche |
|
 |
|
| Appunti tecniche |
|
| Visite: 3065 | Gradito: |
Leggi anche appunti:Adc 0804ADC 0804 Convertitore A/D con visualizzazione esadecimale su due display Schema elettrico Strumenti utilizzati ADC0804; varie Realizzazione di reti combinatorie dati problema o tabella di verita'RELAZIONE DI LABORATORIO DI ELETTRONICA TERZA Le energie rinnovabiliLE ENERGIE RINNOVABILI L'energia presente sul pianeta arrivava per il 99% dall'esterno |
 |
 |
Dicesi tempo di risposta della macchina il ritardo Δ=tj-ti con il quale una variazione dell'ingresso è seguita dalla conseguente variazione sull'uscita.
Dicesi elemento di ritardo puro Δ una macchina ideale la cui uscita U al tempo t+Δ è uguale all'ingresso I al tempo t, per qualsiasi valore di t≥0
U(t + Δ) = I(t) (1.2)
L'elemento di ritardo puro (a) è un' astrazione che può rappresentare, a seconda dei casi, ritardi parassiti di un'apparecchiatura reale oppure elementi fisici appositamente costruiti per ritardare l'azione di una macchina.
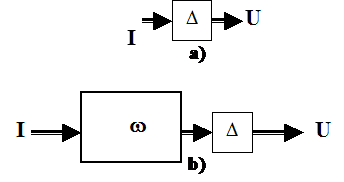
a) Elemento di ritardo puro; b) Macchina combinatoria con ritardo
Dicesi elemento di ritardo inerziale l'elemento che, sollecitato all'istante t da una variazione dell'ingresso, non 'sente' tale variazione se essa non permane all'ingresso almeno per un tempo E e la segue sull'uscita (sempre che duri almeno E) solo dopo un tempo E;
Il fenomeno è analogo a quello di una forza applicata per un tempo breve ad un corpo: il corpo resta fermo a causa della sua inerzia.
Nel caso che un elemento richieda una durata E del segnale in ingresso per 'sentirlo' e causi un ritardo E'>E, si puù schematizzare con un elemento di ritardo inerziale E seguito da uno di ritardo puro D=E'-E
I vincoli sulla durata minima di un segnale imposti dal fenomeno del ritardo inerziale consentono anche di determinare la frequenza massima di un segnale binario in ingresso ad una macchina; infatti, se il segnale è binario, la sua variazione può avvenire al minimo con periodo 2E e quindi la sua frequenza massima è
fmax = ![]()
Valore impulsivo in un istante
Si dice che all'istante tk il valore ik è impulsivo se esiste un valore iko e due istanti t1 e t2 tali che:
I(tk) = ik
I(t) = ik0 t: (t1
≤ t < tk) ![]() (tk < t ≤ t2)
(tk < t ≤ t2)
ik0 è detta base di ik
In altri termini, se ik è impulsivo all'istante tk, I assume in un intorno di tk la sequenza dei valori
ik0ikik0 (2.2)
in cui ik permane un solo istante.
Valore impulsivo in un intervallo
Posto t2
- t1 =![]() t il valore impulsivo
ik dicesi impulsivo con base ik0 nell'intervallo
di tempo
t il valore impulsivo
ik dicesi impulsivo con base ik0 nell'intervallo
di tempo ![]() t
t
Valore a livelli (in un istante o in un intervallo) .
Un valore I(tk)=ik si dice a livelli se è assunto anche in un intorno dell'istante tk
In altri termini, per un valore a livelli si ha
I(t) = ik t: (t1 ≤ t < tk )![]() (tk < t ≤ t2) (3.1)
(tk < t ≤ t2) (3.1)
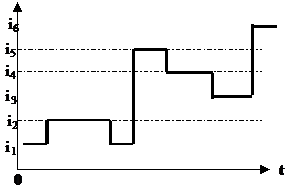
Per fissare le idee in fig. 2.1 è riportato il valore di una variabile astratta a sei stati in funzione del tempo.
L'intervallo che interessa è quello di funzionamento di una macchina ed in tale intervallo un valore può essere (nell'intervallo (0.T)):
a livelli, come i1 nel diagramma di fig.2.1;
impulsivo, come i3, i4, i6, rispettivamente di basi i2, i5.
basi (a livelli) di impulsi, come i2, i5.
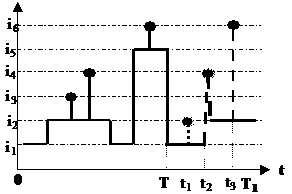
Fig.2.1 Esempio di evoluzione di una variabile a 6 valori
mentre non esistono in pratica (con riferimento all'intervallo (0,T1) di figura)
valori 'misti', cioè a livello in un sottointervallo ed impulsivo altrove, come accadrebbe al tempo t1.di figura;
valori impulsivi raggiunti con la sequenza. ik0iki'k0, cioè non esistono impulsi con valori a livello diversi a destra e sinistra, come al tempo t2 ;
valori impulsivi raggiunti da basi diverse, cioè sequenze ikoikikoi'k0iki'k0., come al tempo t3,
Un valore a livelli incluso in una sequenza può dunque essere la base di un impulso (come i2, i5) o non esserlo (come i1): lo diremo livello-base o semplicemente base nel primo caso, soltanto livello nel secondo.
Una sequenza i cui valori appartengono ad un insieme di valori, I = è in generale composta da
a) valori impulsivi: X =
b) basi: B =
e si dice:
a livelli se contiene esclusivamente livelli;
impulsiva se contiene esclusivamente valori impulsivi e le relative basi;
Il caso di "sequenza mista", contenente cioè livelli, valori impulsivi e basi. (come in fig.2.1) non è preso qui in esame in quanto non interessa le realizzazioni concrete.
I concetti di cui sopra si applicano in particolare (con notevole
semplificazione) ad una variabile booleana x, la quale, potendo assumere due
soli stati, può essere in un intervallo ![]() t:
t:

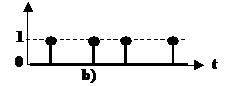
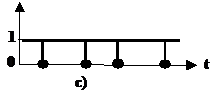
Fig.3.1 - Tempificzione di una variabile binaria:
a) a livelli: b) impulso positivo; c) impulso negativo
-a livelli (fig. 3.1a);
-impulsiva per x = 1 o impulso positivo (fig. 3.1b);
-impulsiva per x = 0 o impulso negativo (fig. 3.1c);
mentre si ricorda che non esistono sequenze miste.
Una particolare variabile binaria impulsiva è il cosiddetto segnale di orologio o clock, costituito idealmente da una sequenza di impulsi (che per semplicità consideremo positivi) ad intervalli equidistanziati di τ nel tempo.
In realtà il clock è ottenuto da un oscillatore e presenta impulsi di periodo τ, frequenza f=1/t.e durata Δ non nulla (fig. 3.2b). Il rapporto d è detto anche duty cycle del segnale di clock.
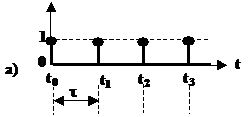

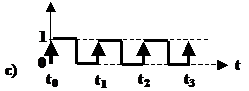

Il clock; a) Schema di principi; b) segnale reale;
c) attivo su fronti di salita; d) attivo su fronti di discesa
Talora, per risolvere alcuni problemi di tempificazione, è necessario disporre di più segnali di clock, ovvero riferirsi a n>1 spazi discreti di tempo, tali che nessun istante appartenga a due spazi diversi Ciò si realizza in pratica mediante n segnali del tipo di fig. 3.2b) ritardati fra di loro successivamente di τ/n: si dice in tal caso che si dispone di un clock a n fasi. Valori tipici di n sono 2 e 4; in fig. 3.3 è riportato un clock a 4 fasi.

Fig. 3.3. Clock a 4 fasi

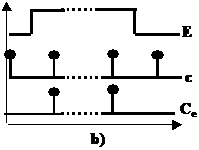
Fig. 3.4 - Evento sincronizzato con il clock
Fig, 4.1- Sequenza a livelli
In una sequenza a livelli (fig. 4.l) tutti i valori sono a livello: ciascun valore rappresenta un differente 'evento' ed è significativo nella sequenza; questa va interpretata con riferimento allo spazio continuo del tempo, nel senso che in ogni istante esiste un valore significativo.
Nelle sequenze impulsive (fig.4.2) non esistono livelli che non siano basi degli impulsi. In realtà, le basi hanno la sola funzione di distanziare fra loro gli impulsi, che sono i soli valori significativi della sequenza e rappresentano gli istanti in cui gli eventi vanno presi in considerazione. La sequenza va interpretata in uno spazio discreto del tempo, definito dagli istanti stessi in cui sono presenti gli impulsi.
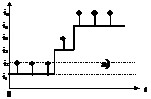
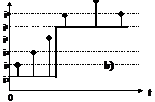

Fig.4.2 - Sequenze impulsive:
a) a sincronizzazione esterna; b) autosincronizzata; c) puramente impulsiva.
Esistono differenti sottomodelli di sequenze impulsive:
Se su ciascuna base della sequenza insiste un unico valore impulsivo, la sequenza è detta 'a sincronizzazione esterna' (fig. 4.2a).
Dopo una base si può presentare il solo impulso che su di essa insiste; la sequenza è del tipo
b1xlb1b1xlb1b2x2b2 b2x2b2b3x3b4...
dove xi è l'unico impulso di base bi. Si può assumere allora la base rappresentativa dell'evento e l'impulso come lo strumento che individua unicamente l'istante in cui l'evento si presenta (se si presenta); l'impulso, in altri termini, svolge solo funzioni di sincronizzazione.
In termini di codifica occorre una sola variabile binaria impulsiva, che svolge, appunto, funzioni di sincronizzazione (clock).
Il nome di 'sincronizzazione esterna' deriva appunto dal fatto che la sincronizzazione è affidata ad una variabile apposita, che non identifica anche gli eventi da elaborare ed è dunque 'esterna' alla logica del sistema.
Se su almeno una base della sequenza insistono distinti valori impulsivi, la sequenza è detta 'autosincronizzata' (fig. 4.2b).
Dopo una base può presentarsi uno qualsiasi degli impulsi che su di essa insistono; la sequenza è del tipo
b1xl1b1b1xl2b1b2x21b2 b2x22b2
dove xij è uno degli impulsi di base bi.
Ciascun valore impulsivo rappresenta un distinto evento ed inoltre svolge funzioni di sincronizzazione in quanto individua l'istante in cui l'evento si presenta.
In termini di codifica occorrono k variabili binarie impulsive, se k è il massimo numero dei valori impulsivi che insistono su una stessa base (cfr.§ 8: gli eventi sono quindi associati ad una combinazione di variabili binarie a livelli ed impulsive: queste ultime distinguono gli eventi fra loro e fungono da variabili di sincronizzazione.
Caso particolare di sequenza autosincronizzata è una sequenza che diremo 'puramente impulsiva': essa è caratterizzata dal possedere una sola base (fig-4.2c):
b xl b x2 bb xn b
Si può dunque assumere b come assenza di eventi, che sono invece rappresentati dai valori impulsivi.
In termini di codifica, come si vedrà, si associa a ciascun valore impulsivo una distinta variabile binaria impulsiva, che diventa rappresentativa di un distinto evento.
Le macchine a livelli operano con riferimento allo spazio continuo del tempo; in particolare, se in ingresso si presenta la sequenza.. i1 i2 i3..., la macchina risponde con la sequenza di uscita ..f(i1) f(i2) f(i3)..con le medesime caratteristiche temporali (fig. 5.1).
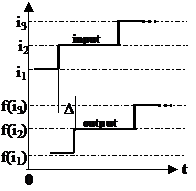
Fig. 5.1 - Macchina a livelli
Le macchine impulsive non sono molto significative come macchine combinatorie autonome, mentre lo sono come macchine combinatorie componenti di macchine sequenziali (vedi capitoli seguenti). Esse operano con riferimento ad uno spazio discreto del tempo, scandito dagli istanti nei quali è presente un valore impulsivo, nel senso che il suo funzionamento è definito solo in tali istanti.
A causa dei ritardi interni e della variazione nel tempo degli ingressi binari di una macchina combinatoria si possono verificare comportamenti anomali della macchina in base ai quali l'uscita viene ad assumere, anche se in brevi intervalli di tempo, valori imprevisti; tali fenomeni vengono genericamente indicati come alee.
Alea combinatoria
Una macchina combinatoria U=f(I} possiede un'alea se in corrispondenza della sequenza di ingressoi1 i2si può avere la sequenza di uscitaf(i1) S f(i2) dove S è una generica sequenza di valori (caso limite, un singolo valore).
Un'alea di questo tipo (combinatoria) è transitoria, nel senso che l'uscita f(i2) viene in ogni caso raggiunta, ma è possibile che nel transitorio da f(i1) a f(i2) la macchina assuma valori intermedi imprevisti.
Nel caso che il fenomeno transitorio influisca su altre macchine pilotate dalla macchina in esame, l'alea deve essere eliminata. Tale eliminazione non può avvenire agendo sul dimensionamento dei ritardi interni ma agendo opportunamente sul progetto logico (sulla codifica degli ingressi e/o sul progetto interno della macchina). È in proposito necessaria la seguente definizione:
Stati adiacenti
Due stati si dicono adiacenti se codificati in modo che differiscano in una sola variabile.
Si ha un'alea multipla se due ingressi consecutivi nel tempo, i1 e i2, non sono adiacenti.
Ad esempio, nella rete a livelli che realizza la funzione equivalenza
(fig. 6.1a), ![]() , la variazione dell'ingresso il = 00 ad i2
= 11 non dovrebbe comportare nessuna variazione di y in quanto è f(i1)=f(i2)=1.
, la variazione dell'ingresso il = 00 ad i2
= 11 non dovrebbe comportare nessuna variazione di y in quanto è f(i1)=f(i2)=1.

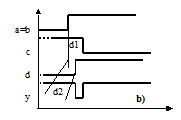
Fig. 6.1 Funzione equivalenza: a) rete logica: b) alea
Viceversa, se le variazioni di a e b non sono simultanee oppure se, pur essendolo, i ritardi interni sono nella relazione d1>d2, si può avere in uscita la sequenza indesiderata1 0 1 Infatti, se entrambi gli ingressi alla porta di uscita assumono il valore 1 per un tempo maggiore del suo ritardo inerziale, in corrispondenza l'uscita y assumerà il valore 0, come esemplificato in fig.6.1b),.
Non vi è modo di eliminare sistematicamente le alee multiple se non con la drastica decisione di evitare transizioni fra ingressi non adiacenti
La concomitanza temporale fra due valori impulsivi binari è un'alea
È questo un caso particolare di alea multipla
Esempi
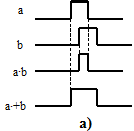

Fig. 6.2 - Esempi di alee per impulsi concomitanti:
a) impulsi sovrapposti; b) impulsi distanziati
Poiché tutte le funzioni sono derivate dalle funzioni somma e prodotto, al fine di evitare i fenomeni aleatori di cui sopra, è necessario che due impulsi in ingresso alla medesima macchina non siano mai concomitanti, se insieme debbono contribuire a determinarne l'uscita.
La concomitanza temporale fra un valore impulsivo binario ed una variazione di livello è un'alea
È dunque necessario, per le sequenze impulsive, che le variazioni di livello delle variabili avvengano in istanti diversi da quelli in cui aavvengono gli impulsi.
In sequenze impulsi, viceversa, non costituiscono alea variazioni concomitanti di variabili binarie e livello, in quanto laddove variano i livelli (a distanza dagli impulsi) non è significativa l'uscita della rete ed eventuali valori aleatori non producono effetti.
Una macchina combinatoria U=f(I} possiede un'alea statica se, detti i1,
i2 due ingressi adiacenti tali che f(i1)=f(i2,)
l'uscita può assumere nel transitorio il valore ![]() .
.
La transizione fra ingressi adiacenti non garantisce infatti, da sola, l'assenza di alee.
Esempio
![]()
|
|
|
|
|
|
|
c |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) |
|
|
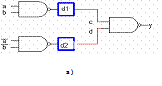
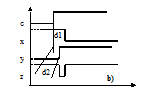
Fig.6.3 - Alea statica: a) esempio; b) tempificazione; c) mappa di Karnaugh
Come evidenziato dall'esempio, l'alea è dovuta al fatto che l'1 della porta di uscita è sostenuto, prima e dopo della transizione, da due porte, corrispondenti a due implicanti distinti della funzione (cfr.fig. 6.3b); d'altro canto, la transizione fra due ingressi adiacenti è certamente contenuta in un implicante, eventualmente non essenziale (nell'esempio ab). Aggiungendo alla rete la porta associata a tale implicante, l'uscita viene da questa tenuta alta durante la transizione e viene meno la causa che provocava l'alea.
Con riferimento all'esempio di fig. 6.3 è dunque sufficiente aggiungere alla u il termine ab
![]()
Le considerazioni sviluppate sull'esempio sono del tutto generali. Si può infatti dimostrare che
Una rete a due livelli AND-OR (o NAND) è esente da alee statiche se e solo se tutti gli implicanti contenenti le transizioni fra gli '1' adiacenti della funzione associata costituiscono altresì porte di primo livello della rete.
La rete è inoltre esente da alee statiche per transizioni fra '0'.
Una macchina combinatoria U=f(I) possiede un'alea dinamica se, detti i1, i2 due ingressi adiacenti tali che f(i1)=a, f(i2)=b¹a , la transizione dei valori sull'uscita u avviene con una sequenza del tipo
L'alea dinamica si verifica soltanto in reti a più di due livelli e si può dimostrare che è un fenomeno risultante da una o più alee statiche contenute nelle sottoreti a due livelli. Ad esempio (fig. 6.4a), in una rete a 3 livelli
![]()
![]()
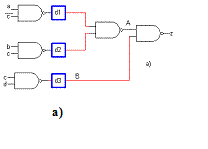
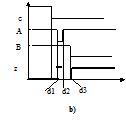
Fig.6.4 - Alea dinamica: a) esempio; b) tempificazione
si verifichi la transizione 1110→1100. Il primo fattore della NAND di uscita possiede un'alea statica (variazione 1→0→1 nel punto A), mentre il secondo (punto B) è soggetto all'unica variazione 1→0; se la variazione in B ritarda rispetto al transitorio in A (fig. 6.4b) si può avere in z la variazione 1→0→1→0.
I vincoli imposti dai fenomeni legati alle alee, nell'ipotesi che queste siano influenti sul comportamento del sistema in cui la macchina è inserita, condizionano la codifica degli ingressi.
Per le macchine a livelli, detto N il numero degli stati di ingresso, la codifica potrebbe effettuarsi con il numero di variabili binarie minimo, pari a:
n = (7.1)
Peraltro, non sempre è possibile una codifica minima priva di alee multiple.
Per effettuare una codifica priva di alee è opportuno tracciare, sulla base dei dati del progetto, un grafo delle transizioni, cioè un grafo i cui nodi rappresentano gli stati e gli archi le transizioni fra di essi. Per una macchina a quattro stati con le transizioni i1→i2, i2 → i3, i3→i4, i4→i1 si ha ad esempio il grafo di fig. 7.1a), per una macchina a tre stati quello a tratto pieno di fig. 7.1b).
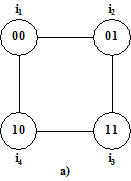
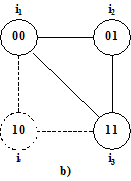
Fig. 7.1 - Esempi di grafo delle transizioni:
a) a 4 stati; b) a 3 stati, con aggiunta di un quarto
La possibilità di assegnare una codifica priva di alee mantenendo inalterati i dati del progetto originario è legata alla struttura topologica del grafo delle transizioni.
Occorre allora procedere a tecniche di assegnazione che alterino il progetto originario; in particolare si adoperano le seguenti tecniche:
a) Forzare la transizione fra due stati che risultassero non adiacenti attraverso stati adiacenti.
Se, ad esempio, in fig. 7.1a) fosse prevista anche la transizione i1→i3, si potrebbero alterare i dati del progetto originario, in modo che tale transizione avvenga come i1→i2→i4. Ovviamente, tale soluzione è possibile solo in casi particolari; con riferimento all'esempio, ciò si verifica se il nuovo stato di uscita f(i2) che così viene ad aggiungersi nella transizione il→i3 non influisce sul sistema nel quale la macchina è inserita, o perché uguale ad f(i1), o perché uguale ad f(i3) o perché indifferente sul comportamento del sistema.
b) Aggiungere nuovi stati di ingresso alla macchina in modo che il grafo delle transizioni consenta un'assegnazione priva di alee.
Ad esempio, per il grafo di fig. 7.1b) si potrebbe aggiungere lo stato i' e modificare la transizione il→i3 in il→i'→i4. Tale soluzione è sempre possibile, poiché per il nuovo stato inserito potrà sempre porsi f(i')=f(i1) oppure f(i')=f(i3) e quindi mantenere inalterata rispetto al progetto originario la sequenza delle uscite.
Con l'aggiunta di nuovi stati, solo in casi banali come quello esemplificato è ancora possibile un'assegnazione minima, mentre nel caso più generale è necessario aumentare il numero di variabili. È stato dimostrato che con un numero di variabili pari a 2N+1 è sempre possibile un'assegnazione priva di alee e sono stati anche studiati metodi per realizzarla
Detti:
- Nb: numero delle basi della sequenza di stati,
- Nx: numero complessivo di stati impulsivi,
k: numero massimo di stati impulsivi che insistono su una stessa base,
la codifica avverrà in generale attraverso:
- m: variabili binarie a livello,
- n: variabili binarie impulsive,
Si ricorda poi che per le sequenze impulsive, i vincoli da alea sono (§§ 6.3, 6.4):
due variabili binarie impulsive non sono mai concomitanti,
le variabili binarie a livello non variano in concomitanza con le variabili impulsive,
le variabili binarie a livello possono variare simultaneamente.
Nel caso più generale, corrispondente alla sequenza autosincronizzata, si ha
m = ([log2 Nb]}; n = k (8.1)
Ad esempio (fig. 8.1) con 2 stati a livello e 3 impulsivi, si ha m=1 (una variabile a livelli b n=2 (due variabili impulsive, xl e x2); con b=0 si ha il≡xl i2≡x2, con b=1 si ha i3≡xl
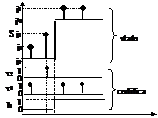
Fig. 8.1 Codifica per sequenza autosincronizzata
Per le sequenze sincronizzate dall'esterno. essendo k=1, la codifica avviene con una sola variabile impulsiva ed m a livelli. Le combinazioni di valori delle m variabili a livello rappresentano gli eventi e la variabile impulsiva (che diremo c) scandisce lo spazio dei tempi TD: essa funge da variabile di sincronizzazione. La variabile binaria c è di solito il segnale di clock o una variabile sincrona con esso.
A titolo di esempio, in fig. 8.2 è mostrata la codifica per una macchina con Nx=Nb=3: sono adoperate 1 variabile impulsiva, c, e variabili a livello, bl e b2. Si noti la simultanea variazione da 0 a 1 delle due variabili a livelli: essa non da luogo ad alea trattandosi di sequenza impulsiva.

Fig. 8.2 Codifica per sequenza sincronizzata dall'esterno
Per le sequenze puramente impulsive, essendo Nb=1 k=Nx, la codifica avviene con nessuna variabile a livelli (m=0) ed n=Nx variabili impulsive, donde anche il nome assegnato alla sequenza; ciascun impulso rappresenta separatamente un evento distinto e funge altresì da sincronizzatore. Ad esempio (fig. 8.3), per una macchina con 3 stati impulsivi ed unica base, si ottiene la codifica con 3 impulsi binari distinti xl, x2, x3
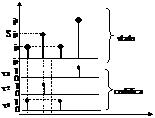
Fig. 8.3 Codifica per sequenza puramente impulsiva
A causa dei vincoli imposti alle variabili di ingresso delle macchine impulsive, le funzioni booleane mediante le quali si esprimono le variabili di uscita assumono una forma particolare. Ciascuna delle funzioni di uscita può essere infatti espressa genericamente come y=f(X, L) ove X è l'insieme delle variabili impulsive ed L di quelle a livello ed, esistendo la condizione di vincolo sulla non concomitanza di due variabili impulsive, si ricade nel caso illustrato nella (II.2.4??): la funzione si può esprimere in forma linearizzata rispetto agli impulsi. Più in dettaglio, si può procedere come segue.
Si esprima dapprima in algebra di Boole la proposizione 'lo stato di uscita assume il valore impulsivo i' come funzione logica degli ingressi binari X, L. A causa delle condizioni di vincolo, tale funzione assume la forma della (II.12.4??), nella quale inoltre il primo termine è nullo in quanto essa è alta solo in corrispondenza degli impulsi; si ha dunque:
'uscita assume valore
i″ = ![]() (9.1)
(9.1)
Anche l'uscita è codificata attraverso variabili impulsive (che diremo Y) ed a livelli (M): ciascuno dei valori i dello stato di uscita è codificato con una combinazione di valori delle Y e delle M e porremo aik=1 (= 0) se la variabile k-esima (a seconda dei casi una y o una m) è codificata alta (bassa) per il valore i. Le variabili impulsive yk saranno dunque alte per tutti gli stati i per i quali si abbia aik=1; considerando la (9.1) si ha:
![]() (9.2)
(9.2)
Per una variabile a livelli la forma è simile, ma la funzione non dipende dalle variabili impulsive xj, dovendo il suo valore rimanere costante a sinistra, a destra ed in concomitanza dell'impulso; la forma è dunque quella della (9.2), dalla quale peraltro è assente l'ingresso impulsivo:
![]() (9.3)
(9.3)
Le forme (9.2) e (9.3) valgono nel caso più generale di un numero qualsiasi di variabili impulsive ed a livelli (sequenze autosincronizzate con almeno due basi) e trovano diverse semplificazioni nei casi di sequenze sincronizzate dall'esterno oppure puramente impulsive in input o in output. Ad esempio, se ingresso e uscita sono entrambi a sincronizzazione esterna, si avrebbe
![]() (9.4)
(9.4)
ove la funzione F (che sinteticamente indica la somma in i delle fi0) identifica per quali valori delle variabili L all'impulso in ingresso x0 corrisponde quello in uscita y0; se, come spesso avviene, ad ogni impulso in ingresso corrisponde quello in uscita, si avrebbe ovviamente F=l e
y0 = x0
Al di la comunque del dettaglio delle forme, interessa sottolineare che esse consentono di ricondurre in ogni caso il progetto combinatorio delle macchine impulsive al progetto delle sole variabili a livello: per ciascuna variabile binaria impulsiva occorre progettare una funzione delle variabili a livello (eventualmente identicamente 1) per la quale moltiplicarla. Esse pongono altresì in evidenza che il progetto concettuale delle macchine è indipendente dalla codifica adottata e che, una volta scelta la natura della sequenza in uscita, si possono in ogni caso esprimere sul piano astratto le condizioni logiche (funzioni degli ingressi) che determinano l'emissione in uscita di determinati valori. Una volta codificati i valori a mezzo di variabili binarie, ne derivano direttamente le espressioni da applicare alle singole variabili.
Come si è visto, il ricorso a macchina ad impulsi o a livelli è determinato da un lato dalla natura dei fenomeni da trattare e dall'altro da esigenze di tempificazione. Queste stesse esigenze possono richiedere che uno o più stati di ingresso siano trasformati da livello a impulso o viceversa; tali trasformazioni vengono effettuate in realtà sulle variabili binarie con le quali gli stati sono codificati e dunque si riconducono alla creazione di un impulso binario da un livello o, viceversa, di un livello da un impulso binario.
La variazione di un livello può essere trasformata in un impulso mediante un derivatore booleano, che si può così definire:
Un derivatore booleano è una macchina che produce un impulso in corrispondenza di una variazione di livello.
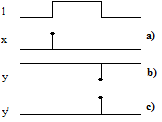
Fig.10.1 - Impulso derivato da una variazione di livello
In particolare può aversi un derivatore del fronte di salita (fig.
10.la), se l'impulso è positivo ed è ottenuto in corrispondenza della
variazione 0→1 (x=dl/dt), un derivatore del
fronte di discesa (fig. 10.lb) se l'impulso è negativo ed è ottenuto in
corrispondenza della variazione 1→0 (y=dl/dt) oppure il suo
negato, considerando sempre positivo l'impulso, ![]() (fig. 10.1 c). È
immediata l'analogia con il derivatore classico ed è dunque giustificato il
nome attribuito a tale apparecchiatura; è anche evidente che l'aggiunta di
appositi invertitori all'ingresso o all'uscita del derivatore consente di
creare qualsiasi combinazione fra variazioni di livello e polarità di impulso.
(fig. 10.1 c). È
immediata l'analogia con il derivatore classico ed è dunque giustificato il
nome attribuito a tale apparecchiatura; è anche evidente che l'aggiunta di
appositi invertitori all'ingresso o all'uscita del derivatore consente di
creare qualsiasi combinazione fra variazioni di livello e polarità di impulso.
Gli schemi di cui sopra sono del tutto teorici; diverse sono le tecniche per ottenere l'impulso dalla variazione di livello. La più diffusa è quella di usare particolari apparecchiature sensibili ai fronti di variazione della variabile a livello (edge triggered, cfr. in seguito, reti sequenziali); per queste apparecchiature il fronte di variazione della variabile a livelli equivale ad un impulso (fig. 10.2). Esistono apparecchiature sensibili ai fronti di salita (variazione 0 positive edge triggered, fig. 10.2a) ed ai fronti di discesa (variazione 1 negative edge triggered, fig. 10.2b)
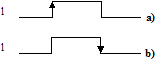
Fig.10.2 - Impulso coincidente con una variazione di fronte
a) fronte di salita; b) fronte di discesa
In altri casi, da una variazione di livello si ricava un effettivo segnale binario che viene appunto considerato un impulso. È da considerare che nella realtà fisica un impulso non ha durata nulla, ma una durata D 0 'abbastanza breve' e segue la variazione di livello dopo un ritardo d, Esiste appunto una apparecchiatura elettronica, detta monostabile (one-shoot), che genera appunto un impulso con le caratteristiche di cui sopra.
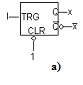

Fig. 10.3 - Monostabile: a) simbolo; b) tempificazione
In particolare, l è l'ingresso 'trigger': l'apparecchiatura è
attivata sul fronte di salita del segnale l; Q (x) è l'impulso di uscita. ma
esiste anche il suo negato, ![]() ; l'ingresso CLR (clear), in figura posto identicamente ad 1,
è un segnale che, se =0, azzera x, ponendo x=0 e quindi azzerando l'impulso. In
effetti, il modello presentato in figura è uno di quelli possibili, ma sono
possibili varianti sulla polarità e la varietà dei segnali.
; l'ingresso CLR (clear), in figura posto identicamente ad 1,
è un segnale che, se =0, azzera x, ponendo x=0 e quindi azzerando l'impulso. In
effetti, il modello presentato in figura è uno di quelli possibili, ma sono
possibili varianti sulla polarità e la varietà dei segnali.
Un impulso può essere un input di comando di una speciale macchina sequenziale - il flip-flop - che ha la proprietà di memorizzare l'impulso trasformandolo in un valore che permane nel tempo. Come si vedrà ampiamente in seguito, esistono due tipi di flip-flop[1]:
il flip-flop trigger (fig. 10.4 a), la cui uscita l cambia valore in corrispondenza di ogni impulso t (fig. 10.4b);
il flip-flop set-reset (fig. 10.4 c), con due ingressi: set pone Q=1, reset pone Q=0 (fig. 10.4 d).
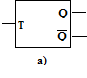
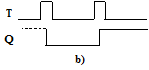
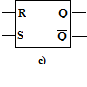

Fig. 10.4 Trasformazione impulso-livello:
a,b) con flip-flop trigger; c,d) con flip-flop set-reset
Per concludere, è utile ribadire che l'impulso visto come evento di durata nulla è solo una astrazione utile per inquadrare il funzionamento delle macchine in modelli astratti; nella realtà, l'impulso ha sempre una durata finita, ma il concetto che esso esprime è che, indipendentemente dalla sua durata, un impulso individua univocamente un 'istante' dello spazio dei tempi e non un 'intervallo' ed è quindi 'come se' fosse di durata nulla. Questa problematica è di limitato interesse per le macchine combinatorie, ma assume notevoli riflessi per le macchine sequenziali trattate nei capitoli seguenti.
Eliminare il § ????
In questo paragrafo si riepilogano i concetti di tempificazione esposti con riferimento ai problemi inerenti il progetto di macchine combinatorie, riprendendo le varie fasi del progetto illustrate nel capitolo IV.
All'atto della definizione della macchina, vengono esaminati i problemi di interazione con le altre macchine del sistema e la natura della macchina (se a livelli o ad impulsi) viene pertanto identificata anche dai problemi di sincronizzazione fra le macchine.
In caso di progetto di parti di un sistema già definito nella sua struttura fondamentale, è già noto se il sistema è dotato di clock ed a quante fasi oppure se comunque esistono variabili binarie da adoperare per la tempificazione.
Viceversa, nel caso di un progetto ex-novo di un sistema, tali scelte vanno predefinite in funzione delle esigenze delle singole macchine componenti, della natura degli ingressi primari e soprattutto degli aspetti più vincolanti circa la tempificazione, derivanti dalla presenza di macchine sequenziali (cfr. capitoli successivi) da inserire nel sistema. Per la maggiore semplicità di progetto, si preferisce in genere adoperare macchine impulsive; con tale scelta si superano alcuni problemi di alee insiti nell'adozione di un modello a livelli.
In particolare, l'aggiunta di un segnale di sincronismo ad una macchina a livelli e quindi la sua trasformazione in macchina sincronizzata dall'esterno risolve i problemi di alee multiple altrimenti ineliminabili. Infatti la macchina ad impulsi non presenta il problema delle alee multiple, in quanto, in corrispondenza della variazione di uno o più livelli, presenta un'uscita costante, mentre in corrispondenza dell'impulso di sincronismo (non concomitante con le variazioni di livello) la macchina fornisce in uscita un impulso contenente in sé l'informazione desiderata.
Con riferimento alla semplice rete di cui alla fig. 6.1 si può ad esempio porre
![]()
con c1 impulso di clock e far sì che le variazioni di livello avvengano con sfasamento sufficiente rispetto a c1 (ad esempio in sincronismo con l'altra fase c2 di un clock bifase). Nell'insieme TD definito da cl si hanno i valori corretti (y(00)=y(11) =1) mentre eventuali ritardi fra le variazioni di x1 e x2 vengono 'assorbiti' dal fatto che, essendo cl=0, l'uscita resta sempre nello stato 0.
Il problema della codifica (se non è già definito implicitamente dal punto A) consiste in quanto illustrato nei §§ 7 e 8. Si noti pertanto che:
- per le macchine a livelli, la codifica interessa tutti gli stati di ingresso ed occorre evitare alee multiple tra tutte le variabili di ingresso;
- per le macchine ad ingressi puramente impulsivi, la codifica è già implicita nei vincoli sulle variabili di ingresso;
- per le macchine a sincronizzazione esterna, la codifica riguarda tutte le variabili a livello e le funzioni di uscita vanno poi poste in AND con l'impulso di tempificazione;
- per le macchine autosincronizzate, le variabili binarie impulsive di ingresso sono assegnate e la codifica interessa soltanto le variabili a livello.
Per le reti a livello, il progetto deve essere realizzato eliminando, ove necessario, le alee statiche: le reti a livello si adoperano solo dopo un'attenta analisi nell'assegnazione dei codici in quanto possono essere soggette ad alee multiple e statiche.
Per le reti ad ingressi impulsivi, il progetto si realizza in base alle (9.2) e dunque si può condurre il progetto ricercando esclusivamente la forma delle fii(L) per ogni funzione di uscita e moltiplicando poi ciascuna di queste per un differente impulso xj.
Nella scelta della forma algebrica, vanno tenute in conto le considerazioni relative al compromesso costo-velocità per quanto attiene al numero di livelli (cfr. § 1). Va inoltre considerato che per le macchine impulsive il numero complessivo di livelli è legato essenzialmente alla forma algebrica delle fii(L) ed alle modalità di realizzazione delle (9.2) o delle (9.3).
In particolare, il prodotto x·fii(L) può essere ottenuto realizzando fij(L) e successivamente moltiplicandola per l'impulso oppure distribuendo l'ingresso impulsivo su tutte le porte di primo livello.
Con riferimento al tipo di realizzazione (NAND, NOR,) in dipendenza della funzione utilizzata, (9.2) o (9.3), si rimanda a quanto illustrato in IV.5.
Abramson, N.M., Information Theory and Coding, Mc Graw-Hill, 1964.
Breeding, K.J., Digital design fundamentals, Prentice-Hall, 19810.
Cerny, E. e Marin, M.A., 'An approach to Unified Methodology of Combinational Switching Circuits', IEEE Trans. Computers, 26, (1977).
Huffman, D.A., 'The Design and Use of Hazard-Free Switching Networks',Journ. of ACM, 4 (1957).
Marcus, M.P., Switching Circuitsfor Engineers, Prentice-Hall, 1976.
Mc Cluskey, EJ., 'Transients in Combinational Logic Circuits' in Redundancy Techniques far Computing Systems, Spartan Book, 1962.
Zisapel, Y., Krieger, M. e Kella, J., 'Detection of Ha:zards in Combinational Switching Circuits', IEEE Trans. Computer, 28 (1979).
 |
| Appunti su: |
|
| Appunti Ingegneria tecnico |  |
| Tesine Gestione |  |
| Lezioni costruzione |  |