 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3993 | Gradito: |
Leggi anche appunti:La statisticaLA STATISTICA DEFINIZIONE La statistica consiste nell'analisi quantitativa Rappresentazioni grafiche di variabili statisticheRAPPRESENTAZIONI GRAFICHE DI VARIABILI STATISTICHE Occorre fare una distinzione Appunti statisticaAPPUNTI STATISTICA STATISTICA: Il termine deriva da static, nasce nel XVII |
 |
 |
APPUNTI STATISTICA
STATISTICA: Il termine deriva da static, nasce nel XVII secolo grazie a Graunt, un medico inglese che studiò il numero di nascite e di morti relative ad una certa parrocchia. La statistica veniva considerata scienza dello stato in quanto serviva per governare, nonostante la nascita venga fatta risalire a Graunt la statistica è sempre esistita ne sono un esempio i censimenti. È la scienza che studia numericamente i fenomeni collettivi. I maggiori statisti della storia son Pascal e La Place.
INDAGINE STATISTICA: consiste nel porsi una domanda , tra tutti i vari aspetti che voglio analizzare scegliere quelli dai quali posso ricavare un dato numerico, ed individuare la popolazione (insieme degli elementi su cui vado ad indagare es: studenti).
STATISTICA DESCRITTIVA: si ha quando lavoriamo con tutta la popolazione.
STATISTICA INFERENZIALE: si ha quando lavoriamo con un campione (parte della popolazione)
UNITA' STATISTICA: ogni componente del gruppo.
UNITA' DI RILEVAZIONE: è un gruppo (es: all'interno della scuola possono essere le classi).
Avviata l'indagine statistica procedo con la rilevazione dei dati attraverso interviste, questionari, interviste telefoniche, dati ISTAT ecc. ecc. dai quali ottengo dei dati grezzi.
CARATTERI CHE RAPPRESENTANO UN FENOMENO: possono essere sia di natura quantitativa che qualitativa.
![]() QUALITATIVA Sono tutti i
caratteri espressi mediante aggettivi, vengono definiti mutabili e possono essere ordinabili o meno (es: non
c'è ordine tra maschio e femmina ma c'è nei titoli delle licenze scolastiche elementare, media.)
QUALITATIVA Sono tutti i
caratteri espressi mediante aggettivi, vengono definiti mutabili e possono essere ordinabili o meno (es: non
c'è ordine tra maschio e femmina ma c'è nei titoli delle licenze scolastiche elementare, media.)
![]()
![]() DISCRETI: sono i numeri interi.
DISCRETI: sono i numeri interi.
![]() QUANTITATIVA
tutti vengono definiti variabili
QUANTITATIVA
tutti vengono definiti variabili
CONTINUI: rappresentano tutti i numeri reali.
Il trattamento di questi dati viene definito spoglio e organizzazione. Il primo passo è quello di costruire una tabella di distribuzione:
|
carattere |
Frequenza assoluta |
|
1°modalità |
xxx |
|
2°modalità |
xxx |
|
3°modalità |
xxx |
FREQUENZA ASSOLUTA: è il numero di casi in cui compare la modalità sull'intera popolazione
esempio:
Alunni 25 di cui 15 maschi e 10 femmine
|
sesso |
Frequenza assoluta |
|
maschio |
|
|
femmina |
|
|
totale |
|
Nei
caratteri quantitativi continui si parla di distribuzione per classi di
frequenza, per trovare il numero della classi si deve fare la radice della
popolazione ad es: se ho una popolazione di 25 elementi le classi saranno 5 in
quanto![]() = 5
= 5
esempio:
altezza di 9 ragazzi: 156, 167, 170, 162, 158, 169, 167, 161,159
|
altezza |
Frequenza assoluta |
|
|
|
|
|
|
|
|
|
Dopo aver trovato la frequenza assoluta posso trovare la frequenza relativa che si ricava dal rapporto tra la ferq. Assoluta e l'intera popolazione.
Esempio:
|
sesso |
Frequenza assoluta |
Frequenza relativa |
|
maschio |
|
|
|
femmina |
|
|
|
totale |
|
|
* la somma della frequenza relativa dv essere sempre 1 o il più vicino possibile
E' possibile inserire pure la frequenza percentuale che si ricava moltiplicando la freq. Relativa per 100
Esempio:
|
sesso |
Frequenza assoluta |
Frequenza relativa |
Frequenza percentuale |
|
maschio |
|
|
0,6 x 100 = 60% |
|
femmina |
|
|
0,4 x 100 = 40% |
|
totale |
|
|
|
Se voglio paragonare 2 gruppi sulle stesse cose devo paragonare le percentuali.
Altri aspetti importanti sono la frequenza assoluta cumulata e la frequenza relativa cumulata che servono per trovare i cosiddetti percentini.
|
altezza |
Freq. assoluta |
Freq. relativa |
Freq. % |
Freq. cumulata |
Freq. rel. cumulata |
|
|
|
|
|
|
|
|
|
|
|
|
= 5 |
= 55% |
|
|
|
|
|
= 9 |
= 99% |
|
Totale |
|
|
|
|
|
La tabella non è immediata, un maggiore impatto viene dato attraverso i grafici, i più frequenti sono quelli a nastro che possono essere sia verticali che orizzontali.
AREOGRAMMI: si chiamano così in quanto l'area della figura è proporzionale alla frequenza, i principali sono:
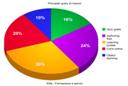 grafici a torta: si possono usare per qualsiasi cosa l'importante è che
il numero degli spicchi non sia troppo elevato.
grafici a torta: si possono usare per qualsiasi cosa l'importante è che
il numero degli spicchi non sia troppo elevato.
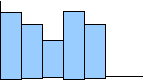
Istogrammi: serve per rappresentare le classi di frequenza: quando le classi sono continue l'ampiezza delle colonne è uguale, quando le classi hanno ampiezza diversa anche le colonne avranno larghezza diversa (la larghezza delle colonne deve essere proporzionale a quella delle classi).
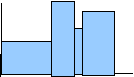
INDAGINI CENTRALI E DI DISPERSIONE: sono dei valori che sintetizzano il dato.
MEDIA: è la somma di tutti i valori numerici divisi per la quantità.
MODA: è la classe di frequenza più numerosa ( viene usata per i dati qualitativi non ordinabili).
MEDIANA: è il valore che corrisponde al valore centrale es: 0 1 4 7 9 se i numeri sono pari sommo i due valori centrali e li divido per 2 es: 1 8; 3 + 6 = 9; 9/2 = 4,5. Per trovare la mediana con le classi ho bisogno della frequenza relativa cumulata, la classe che ha in sé il 50% è la mediana.
MEDIA: definizione specifica "dati N numeri diciamo loro media un qualunque numero, compreso tra il minimo e il massimo, calcolato utilizzando tutti gli elementi dati e che conservi qualche aspetto quantitativo della distribuzione iniziale ". A seconda del contesto usiamo un diverso tipo di operazione:
media armonica: è il reciproco della media dei reciproci.
1
![]()
![]() media geometrica: è la radice ennesima del prodotto dei termini, il
valore della radice varia a seconda del n° di valori sotto radice.
media geometrica: è la radice ennesima del prodotto dei termini, il
valore della radice varia a seconda del n° di valori sotto radice.
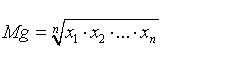
media quadratica: si
sommano i quadrati dei valori, si divide per il numero dei valori , dopo di che
si fa la radice quadrata. (con questo metodo si vuol conservare la somma dei
quadrati)
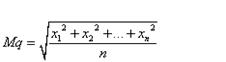
media per classi continue: trovo il valore medio della classe, lo moltiplico per la frequenza poi sommo i valori e faccio la media tra questi.
INDICI DI DISPERSIONE:
campo di variazione: differenza tra valore massimo e valore minimo, se la variazione è piccola tutti i dati sono vicini al valore medio, se è grande la variazione tra i dati è ampia es:
166 - 2 = 164 e 22 - 18 = 4
semi dispersione massima: valore massimo meno valore minimo diviso due es:
22 - 18 = 4 4/2 = 2
scarto medio assoluto semplice: consiste nel fare la sottrazione tra il numero dei dati e la media e prendere il valore assoluto (il numero positivo) di qualsiasi risultato venga. Es:
18 - 20 = -2 ma siccome voglio il positivo allora sarà 2 (praticamente se viene col + lo lascio + se viene col - lo cambio in + ).
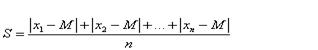
si può pure calcolare rispetto alla moda e alla mediana cambia
solo la M nella formula. Lo
scarto lo prendo per tutti i dati pure quelli che si ripetono.

Scarto quadratico medio: è più noto come deviazione standard,
viene indicato in qualche testo con ![]() (sigma) il suo quadrato si chiama varianza. È famosa perché
si riferisce alla distribuzione normale di Gauss. (Al posto di X andrebbe M
nella formula)
(sigma) il suo quadrato si chiama varianza. È famosa perché
si riferisce alla distribuzione normale di Gauss. (Al posto di X andrebbe M
nella formula)
 |
| Appunti su: appuntimania, ho il numero di addetti e la frequenza percentuale come ricava quella assoluta3F, |
|
| Appunti Spagnolo |  |
| Tesine Francese |  |
| Lezioni computer |  |