 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1563 | Gradito: |
Leggi anche appunti:Significato geometrico della derivataSIGNIFICATO GEOMETRICO DELLA DERIVATA Sia f(x) una funzione definita in Studio del diagramma di una funzioneSTUDIO DEL DIAGRAMMA DI UNA FUNZIONE I risultati fin qui ottenuti ci Il teorema degli incrementi finiti(o di Cauchy)Il teorema degli incrementi finiti(o di Cauchy) Se F(x) e φ(x) |
 |
 |
Per verificare ulteriormente i dati ottenuti è stato scritto un programma che potesse simulare il modello matematico da me ipotizzato. Il suo schema geometrico si rifà a quello usato nella misurazione riportata in figura 9. Esso si divide in due sezioni di codice: la prima, per il calcolo dei punti, scritta in linguaggio C, mentre la seconda, per la visualizzazione, scritta in Matlab.
Calcolo dei punti
Per comodità del lettore abbiamo evidenziato i blocchi principali
![]()
#include<stdio.h>
#include<conio.h>
#include<math.h>
#include<string.h>
#define BMAX 10000
#define Lm 0.2
struct ramo;
FILE *x,*y,*n;
float lc, ld, ls, angdx, angsx, k, d, c, s;
float min(float c, float d, float s)
else
void calcoli(ramo*r,int&i,int&n,int t,int j)
else
else
}
void vis(ramo*r,char*lato,int j,int i)
if(strcmp(lato,'lato sinistro rispetto sua radice')==0 || j==0)
vis(r,'lato destro rispetto sua radice',++j,i);
else
}
void salva(ramo*r,int i)
fclose(x); fclose(y);
main()
while(lc<0);
ld=lc;ls=lc;l=lc;
do while(lm<Lm);
do while(d<0);
do while(c<0);
do while(s<0);
do while(angdx<0 || angdx>180);
do while(angsx<0 || angsx>180);
o=min(c,d,s);
r[0].x[0]=0;r[0].y[0]=0;
r[0].x[1]=l*cos(M_PI/4);
r[0].y[1]=l*sin(M_PI/4);
r[0].ang=45;
if(l>lm)
while(l>lm && i<BMAX); }
else
while(l<lm && i<BMAX); }
printf('nlunghezza ramo piu' piccolo:%fn',l*o);
printf('nnumero rami:%dn',i);
printf('nvisualizzare struttura?(y/n)n');
scanf('%s',&scelta);
if(strcmp(scelta,'y')==0)
vis(r,'radice',0,i);
printf('nsalvare struttura in un file?(y/n)n');
scanf('%s',&scelta);
if(strcmp(scelta,'y')==0)
salva(r,i);
else
printf('npremere un tasto per terminaren');
getch();
![]()
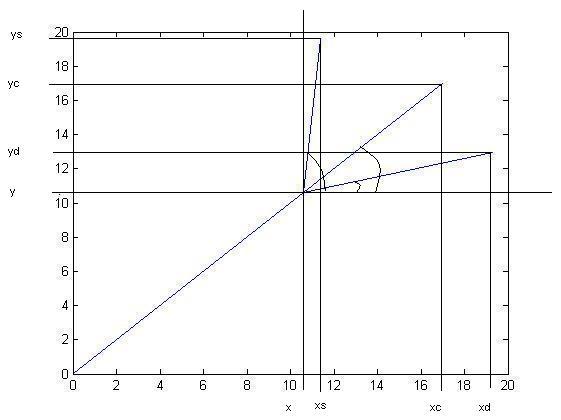
Figura costruzione su matlab del primo gruppo di rami figli a partire da una ramo padre
Visualizzazione Punti
![]()
clear all;
fid = fopen('nfile.dat', 'rb');
[n] = fread(fid,1,'int');
fclose(fid);
n=n*2;
fid = fopen('xfile.dat', 'rb');
[cx] = fread(fid,n,'float32');
fclose(fid);
fid = fopen('yfile.dat', 'rb');
[cy] = fread(fid,n,'float32');
fclose(fid);
for i=1:2:n
plot(cx(i:(i+1)),cy(i:(i+1)));
hold on;
end
![]()
Qui riporto alcune immagini ottenute con il nostro programma. Va precisato che queste immagini sono costruite tramite un modello matematico di rami singoli e che quindi esso non tiene conto né dell'ingombro che i rami incontrano nella loro crescita (costituito dai rami adiacenti) né dei fattori probabilistici presenti a causa del moto browniano.

Figura Simulazione di un ramo costruito con un voltaggio di 2V
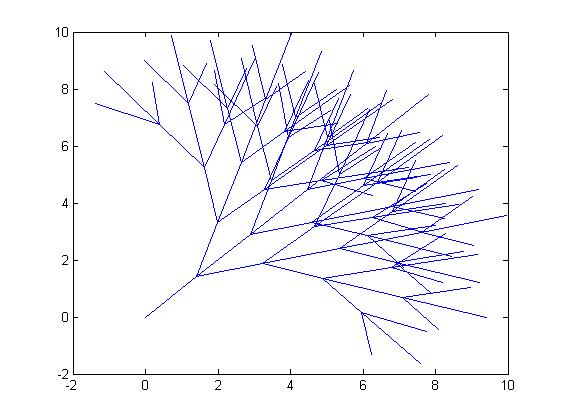
Figura Simulazione di un ramo costruito con un voltaggio di 10V

Figura Simulazione di un ramo costruito con un voltaggio di 18V
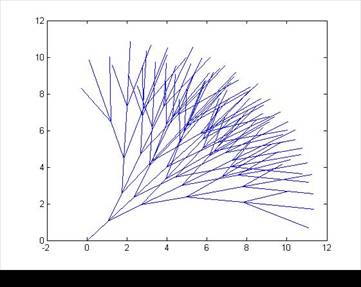

Figura confronto grafico fra un ramo ottenuto a 18V e la sua simulazione ottenuta.
Come si può facilmente vedere dalla figura 27 il risultato grafico delle situazioni da me simulate rispecchia in modo abbastanza fedele la realtà degli aggregati.
Ciò è indice del fatto che il modello matematico sviluppato è una buona approssimazione della situazione dei rami degli aggregati ottenuti tramite DLA e che quindi si presenta come adatto a descrivere la realtà.
RINGRAZIAMENTI:
Ringraziamo l'Istituto E. Breda per i materiali e le apparecchiature forniteci, i miei compagni Giacomo Brogin, Simone Mangano, Iacopo Pancotti e Jacopo Pellegatta per avermi aiutato nel perseguire questo ambizioso obiettivo, tutti i miei professori di quest'anno scolastico, in particolare il prof. Francesco Driglia, tutor della mia area di progetto, per tutto ciò che questo ha comportato, la prof.essa Elisa Brivio e la prof.essa Cristina Perini per il grande tempo dedicatomi e il prof. Fabrizio Favale per i consigli forniti; il prof. David Brynn Hibbert della University Of New South Wales di Sydney, l'ing. Giacomo Favini, l'ing. Matteo Ceserani e il prof. Paolo Brambilla dell'Università degli studi di Milano-Bicocca per l'aiuto datomi ed infine il prof. Francesco Prestipino per avermi incoraggiato nel proseguimento del progetto.
Bibliografia
T. C. Halsey, Diffusion-Limited Aggregation: A Model For Pattern Formation,
<<Physics Today>>, Novembre 2000, 36-41.
H. Jurgens, H. O. Peitgen, D. Saupe, Fractals for the Classroom, Springer-Verlag, 1992.
B. Mandelbrot , Gli oggetti frattali: forma, caso e dimensione, Einaudi, 1987.
B. Mandelbrot , La geometria della natura, 2a ed., Theoria, 1990.
H. O. Peitgen, H. Jürgens, D. Saupe, Chaos and Fractals - New Frontiers of Science, 2nd ed., Springer-Verlag, 2004.
L. Peliti, Appunti di meccanica statistica, Bollati Boringhieri, 2003.
T. Vicsek, Fractal Growth Phenomena, World Scientific, Singapore, 1989.
ENCARTA ENCICLOPEDIA ONLINE
https://it.encarta.msn.com/encyclopedia_761562645/Elettrodeposizione.html
ULTIMA CONSULTAZIONE 12-3-2008
ERCIM NEWS - ONLINE EDITION
https://www.ercim.org/publication/Ercim_News/enw29/vicsek.html
ULTIMA CONSULTAZIONE 12-3-2008
FLAVER - FLASH EXPERIMENTATIONS AND OTHER CURIOSITIES
https://mx.coldstorageonline.com/index.php?bid=53
ULTIMA CONSULTAZIONE 12-3-2008
FRATTALI.IT
https://www.frattali.it/indexnoframe.html
ULTIMA CONSULTAZIONE 12-3-2008
JIM CARLSON'S PAGE
https://xanadu.math.utah.edu/java/brownianmotion/1/
ULTIMA CONSULTAZIONE 12-3-2008
MIORELLI.NET
https://www.miorelli.net/frattali/matematica.html
 |
| Appunti su: |
|
| Appunti Contabilita |  |
| Tesine Geografia |  |
| Lezioni Statistica |  |