 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2276 | Gradito: |
Leggi anche appunti:Risoluzione di una forma differenziale esattaRisoluzione di una forma differenziale esatta Consideriamo la funzione Il concetto di infinitoIl concetto di infinito Il concetto di infinito è sicuramente uno dei concetti Ricerca OperativaRicerca Operativa Introduzione La ricerca operativa si occupa di formalizzare |
 |
 |
Proiezione assonometriche isometriche
Per costruire la proiezione isometrica di un cubo, data la proiezione ortogonale, con le facce parallele e perpendicolari al piano di proiezione, per prima cosa si fa ruotare il cubo attorno al suo asse verticale (perpendicolare al piano H) di un angolo di 45°(fig. 6, nella quale per semplicità il cubo è appoggiato sul piano H)
Quindi si fa ruotate il cubo una seconda volta, attorno all'asse orizzontale (perpendicolare al piano V) di un angolo di 35° come indicato in fig.7.
Come si vede dalla figura, gli spigoli del cubo paralleli rispettivamente agli assi x, y, e z nella proiezione ortogonale, ora formano fra di loro un angolo di 120° e la loro lunghezza viene ad essere ridotta, moltiplicandola per il fattore 0,82, rispetto alla vera lunghezza.
Consideriamo la proiezione isometrica così ottenuta si possono desumere le seguenti considerazioni:
a) gli assi x, y, e z sono a 120 fra di loro;
b) per costruire la proiezione isometrica di un oggetto le rette parallele agli assi x, y e z devono essere poste
parallele agli assi x', y' e z';
c) la lunghezza dei vari segmenti deve essere ridotta moltiplicandola per 0,82.
Per rendere più semplice la costruzione, s'è visto che questo raccorciamento delle dimensioni non è osservato nell'esecuzione dei disegni: se segna allora parallelamente agli assi la vera lunghezza dei vari segmenti.
fig.6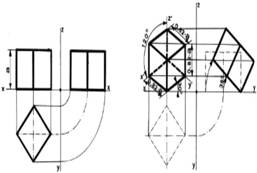 fig.7
fig.7
L'interno di oggetti cavi rappresentato assonometricamente per mezzo di sezioni
L'oggetto è convenzionalmente tagliato con i piani paralleli ai piani di proiezione fig. 8.
Se l'oggetto possiede assi di simmetria, come un prisma, allora si può tagliare un quarto di prisma per mezzo di due piani. I piani di taglio devono essere scelti in modo da presentare una chiara vista delle sezioni richieste.
I cerchi contenuti in piani paralleli ai piani principali di proiezione isometricamente divengono delle ellissi. Si ricorda che l'asse minore di un ellisse deve sempre essere perpendicolare all'asse maggiore.
Se un cerchio è contenuto in un piano parallelo al piano H, come si vede in fig. 9f e 9g, allora l'ellisse avrà l'asse maggiore orizzontale e di conseguenza l'asse minore verticale. Se il cerchio è in un piano parallelo al piano V (fig. 9a, 9b, 9c) l'asse maggiore formerà un angolo di 90° con l'asse y'.
Se il cerchio è contenuto in un piano parallelo al piano W (fig. 9a, 9d, 9e) allora l'asse maggiore forma un angolo di 90° con l'asse x'.
I cerchi possono considerarsi contenuti in quadrati, le cui proiezioni isometriche sono dei rombi; l'asse maggiore dell'ellisse sarà diretto secondo la diagonale maggiore di questi rombi.
Nel costruire le proiezioni isometriche di cerchi si noti che la lunghezza dell'asse maggiore sarà di 1,22 x D, essendo D il diametro del cerchio e l'asse minore eguale a 0,7 x D.
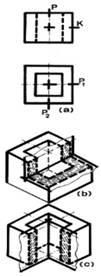

fig.8
fig.9
La proiezione isometrica di una sfera tagliata da diversi piani paralleli ai piani H, V e W
Tracciati gli assi con l'origine delle coordinate coincidente con il centro della sfera, si descrive un cerchi il cui diametro sia uguale a 1,22.D, dove D è il diametro della sfera .
La seconda figura rappresenta una sfera tagliata da quattro piani: due orizzontali, uno verticale ed uno laterale. Le costruzioni sono eseguite nello stesso modo usato per gli esempi precedenti. Le sezioni ottenute con il piano orizzontale superiore sono contornate da segmenti di retta paralleli all'asse. In questo caso ciascuna curva sarà parte di un ellisse o dell'ovale, suo sostituto.
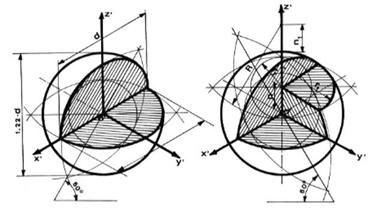 fig.10
fig.10
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Statistica |  |
| Lezioni Fisica |  |