Metodo dei punti di distanza

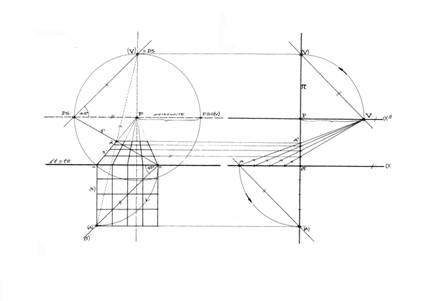
METODO DEI PUNTI DI DISTANZA

Le basi di questo metodo, sono espresse nelle architetture  poco elaborate, del centro di Pomezia.Questo sistema veniva utilizzato dagli artisti del 1400 fiorentino, su indicazioni di F. Brunelleschi. Anche se oggetto di precisazioni dovute allo sviluppo delle scienze matematiche nei secoli, nulla è cambiato sostanzialmente. Esso è fondato sull'utilizzazione dei punti di distanza (punti misuratori) che determinano i valori di scansione prospettica sulle rette ortogonali al quadro. Le rette ortogonali al quadro hanno quale punto di fuga il punto principale P; il cerchio di distanza può essere riguardato come luogo di tutti i possibili ribaltamenti del centro di vista V come luogo di infiniti punti di distanza DS. I punti di distanza delle rette a 45° rispetto a π, appartenenti a piani orizzontali, sono i due punti d'intersezione del cerchio di distanza con la retta di fuga dei piani orizzontali, tutte le corde degli archi di ribaltamento delle rette ortogonali al quadro formano con esso angoli di 45°, la parallela a queste corde per il centro di vista  forma un angolo di 45° con π, DS è il punto di fuga di tali corde, è stato dimostrato che rette fra loro parallele concorrono nello stesso punto, assume molta importanza il ribaltamento è sempre necessario riportare tutti gli elementi su uno stesso piano (quadro), allo scopo passare da costruzioni spaziali (tridimensionali) a costruzioni piane (bidimesionali). Risulta evidente che ogni punto A, nel sistema dei punti di distanza, è individuato da due rette R ed S incidenti, di cui una concorre nel punto principale P ed una concorre nel punto di distanza DS.

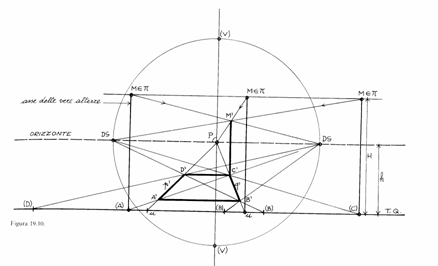
Come esemplificazione, la prospettiva centrale di un quadrato ABCD, si determini l'altezza di un segmento verticale CM. Siano dati la proiezione ortogonale del quadrato ABCD, il segmento CM, la traccia del quadro parallela ai lati AB e CD, la posizione del centro di vista. Si determinano le origini delle rette P e Q sulle quali sono staccati i lati AD e BC, e si ribaltino i vertici A in (A), D (D), B in (B), C in (C).

A questa fa seguito la costruzione prospettica, quindi disegnata la traccia del quadro, l'orizzonte, il cerchio di distanza, le origini delle rette p e q, ed i relativi ribaltamenti (A), (D), (B), (C), e facile descrivere la prospettiva del quadrato. Le rette p'e q', concorrono in P quali immagini di rette ortogonali al quadro, ed i segmenti A'D' e B'C', sono determinati dalla prospettiva delle corde degli archi di ribaltamento, che concorrono nei punti di distanza relativi. Anche le loro immagini prospettiche, A'B', D'C', sono parallele, concorrono in un punto di fuga all'infinito.

Per determinare CM, è necessario individuare la traccia sul quadro del più conveniente fra gli infiniti piani passanti per la retta verticale con origine in C, ed assumere tale traccia quale asse delle vere altezze. Dopodichè, mediante le linee di fuga si desuma M'.