 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1397 | Gradito: |
Leggi anche appunti:La Sezione Aurea - Tra Matematica, Arte e NaturaLa Sezione Aurea Tra Matematica, Arte e Natura A coloro Assonometrie di metricheAssonometrie di metriche Con le proiezioni ortogonali di un cubo, possiamo Schopenhauer, la liberazione nel piacere esteticoSchopenhauer, la liberazione nel piacere estetico Negli scritti di Arthur |
 |
 |
Le medie rientrano, come del resto i rapporti statistici, nella fase dell'elaborazione dei dati, essendo degli indici riassuntivi che permettono di evidenziare le tendenze dei fenomeni studiati.
Passiamo ad esaminare i vari tipi di medie utilizzati in statistica.
La media aritmetica semplice è data dal quoziente fra la somma dei dati di una successione e il numero dei dati stessi.
Supponiamo ad esempio di avere la seguente successione dei dati:
x 1+ x 2+ x3 . + xn , la media aritmetica è data da :
MA= x 1+ x 2+
x3 . + xn = ![]() xi
xi
![]()
![]()
n n
dove il simbolo S indica la somma dei termini xi, con i che assume valore da 1 a n.
Se supponiamo che i termini della precedente successione si presentino con un certa frequenza n possiamo ottenere la media aritmetica ponderata.
Dove le .frequenze n l, n2 . . nn si chiamano pesi
MA= x 1* n l +x
2 * n2+ .
+xn * nn = ![]() xi * ni
xi * ni
![]()
![]()
n l, n2
. . nn ![]() ni
ni
Vediamo un esempio pratico.
N. 10 studenti. di una classe hanno conseguito i seguenti voti in statistica: 6,6,6,7,7,8,8,5,5,4 che riportati in una tabella risultano:
|
Voti xi |
Studenti ni |
|
Totale |
|
![]()
MA= xini = 4*1+5*2+6*3+7*2+8*2 = 62= 6,2
n 10 10
La media aritmetica dei voti è stata 6,2.
Se la tabella anziché voti considera valori divisi in classi od intervalli si può scegliere come xi il valore centrale della classe che possiamo indicare con xi.
Ad esempio se abbiamo una tabella che considera le classi in statura, da cm. 150 a cm. 160, da cm. 160 a 170 e così via, si possono prendere rispettivamente i valori medi cm. 155 e 165.
La media aritmetica gode delle seguenti proprietà
La media geometrica semplice è data dalla radice ennesima del prodotto degli n termini.
Data la successione:
x 1 x 2 . xn la media geometrica sarà:

Supposto che gli xi termini si presentino con una certa frequenza (o peso n si chiama media geometrica ponderata,

ed è la radice che ha per indice la somma dei pesi e per radicando il prodotto dei termini ciascuno elevato al rispettivo peso.
Anche la media geometrica gode di alcune proprietà
La media armonica semplice si può definire come il reciproco della media aritmetica dei reciproci dei termini della successione data.
Data la successione x1, x2, , xn, ricordiamo che la media aritmetica era data da:
MA= x 1+ x 2 . +
xn = ![]() xi
xi
![]()
![]()
n n
per cui la media armonica data la sua definizione sarà :
MAR= n = n
![]()
![]()
1/x1 + 1/x2
+... + 1/xn ![]() 1/ xi
1/ xi
Supposto che gli xi termini della successione si presentino con una certa frequenza (o peso) n si definisce media armonica ponderata.
MARP= n1
+ n2 + ..+ nn = ![]() ni
ni
![]()
![]()
1/x1 * n1 + 1/x2
* n2 +... + 1/xn * nn ![]() 1/ xi * ni
1/ xi * ni
Esempio:
si calcoli la media armonica della successione dei termini 3,5,7,9 ripetuti rispettivamente 2, 3, 5, 6 volte.
|
xi |
ni |
|
|
|
MARP= 2 + 3 + 5 + 6 = 6,043165467
![]()
La media quadratica è la radice quadrata della media aritmetica dei quadrati dei dati
Data la successione xi, x2 x3 la media quadratica sarà data da:
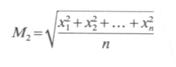
e nel caso della media quadratica ponderata avremo:
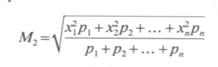
Esempio: la media quadratica dei numeri: 3, 5, 10, 12, 15 è:

Si usa la media quadratica quando si hanno dati positivi e negativi e si vuole eliminare l'influenza del segno.
Esempio:
|
xi |
|
|
Come si vede con la media aritmetica non si ottiene un risultato rappresentativo:
Media aritmetica = ![]()
Se infatti i dati esprimono errori di misurazione, la media ottenuta, cioè -1, non è attendibile perché l'errore minore è 3 e l'errore maggiore è 9, come si vedrà invece, con la media quadratica si ottiene un risultato corretto:
Media
quadratica =![]()
Si definiscono medie lasche quei valori medi che considerano solo alcuni valori della distribuzione.
Vediamone i tipi principali: il valore centrale, la mediàna, i quartili, la moda
Il valore centrale rappresenta il centro del campo di variazione della variabile statistica, in altre parole è dato dalla semisomma dei valori estremi. Data la successione x1 , x 2 , .. , xn il valore centrale è dato da:
v.c.= x 1 + xn
2
dove x1 è il valore più piccolo e xn il valore più grande tra quelli osservati.
La mediana rappresenta il termine che in relazione ad una successione di termini posti in ordine crescente o decrescente, occupa il posto centrale, cioè bipartisce la successione nel senso che lascia ugual numero di termini da una parte e dall'altra. Inoltre se il numero dei termini è dispari la mediana coincide con il termine che occupa la posizione centrale della distribuzione, mentre se il numero dei termini e' pari la mediana coincide con la media aritmetica dei due termini che occupano le posizioni centrali.
Esempio:
nella serie 20, 35, 45, 50, 65 (n dispari) la mediana è data da 45.
nella serie: 15,23,30,40,67,88 (n pari) la mediana è data da 30+ 40 = 35
Nel caso in cui i termini si presentano con una certa frequenza, occorre un calcolo un po' più complicato. Vediamo un esempio chiarificatore.
Data la successione: 2,3,4,5,6 con frequenze (o pesi) rispettivi: 15,13,21,10,11. La somma delle frequenze è 70 e la sua semisomma è 35.
Si procede sommando alla semisomma le frequenze ottenendo:
Si può osservare come la frequenza che rende la somma progressiva delle frequenze uguale o superiore alla semisomma delle frequenze (35) è 21 a cui corrisponde il termine 4 che rappresenta appunto la mediana.
Cioè il trentacinquesimo termine è 4
La mediana gode di 2 importanti proprietà
La definizione di quartile è molto simile a quella della mediana.
Il 1° quartile rappresenta quel valore al di sotto del quale stanno 1/4 dei valori.
I1 2° quartile coincide con la mediana in quanto rappresenta quel valore al di sotto del quale stanno 1/2 dei valori.
I1 3° quartile è quel valore al di sotto del quale stanno i 3/4 dei valori.
Più semplicemente si può anche dire che il 1° quartile è quel valore che bipartisce i termini inferiori alla mediana e il 3° quartile è quel valore che bipartisce i termini superiori alla mediana.
Vediamo un esempio pratico.
Data la seguente successione 1,3,7,9,13,17,23,27,35 determinare il 1°, il 2° e il 3° quartile.
Determiniamo per prima cosa la mediana che coincide con il 2° quartile.
Essendo n dispari:
Me = Q2 = N +1 = 9 + 1 = 10
Cioè il 5° termine, che coincide con 13, è la meridiana.
A questo punto sapendo che il 1° quartile rappresenta il termine che occupa il posto centrale dei dati che stanno a sinistra della mediana, avremo considerando la successione 1,3,7,9 (N pari).
Q1 = 3 + 7 = 10 = 5
2 2
Per quanto riguarda il 3° quartile sapendo che occupa il posto centrale dei dati che stanno a destra della mediana, avremo:
Q3 = 23 + 27 = 50 = 25
2 2
La moda o valore modale può essere definita come il termine che data una seriazione, presenta la frequenza maggiore e si indica con Mo.
Esempio:
|
carattere |
frequenza |
|
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
La moda è rappresentata dal carattere D che presenta la frequenza massima (40).
Ancora più semplice è l'individuazione della moda se ricorriamo ad una rappresentazione grafica:

Come si vede la moda è rappresentata dalla ascissa (D) cui corrisponde l'ordinata massima (40).
A differenza della media aritmetica che può essere anche un termine astratto, la moda è sempre rappresentata da un termine della seriazione.
Rispetto alle medie di calcolo viste nelle precedenti lezioni che considerano tutti i valori di una distribuzione di dati la mediana è preferibile nei casi in cui la successione presenta estremi molto irregolari rispetto ai valori centrali.
Inoltre la mediana e la moda sono di facile determinazione.
 |
| Appunti su: esempio media quadratica, |
|
| Appunti Statistica |  |
| Tesine Geografia |  |
| Lezioni Contabilita |  |