 |
|
| Appunti scientifiche |
|
|
|
| Appunti scientifiche |
|
| Visite: 1105 | Gradito: |   [ Picolo appunti ] |
Leggi anche appunti:Criteri di convergenzaCriteri di convergenza Per stabilire se una serie sia convergente Appunti di disegno tecnico - Due sistemi visivi di rappresentazione graficaAppunti di disegno tecnico Due sistemi visivi di rappresentazione grafica Proiezioni Statistica descrittivaStatistica descrittiva INTRODUZIONE. - Statistica Ramo della matematica che |
 |
 |
Le disequazioni
Disequazioni razionali intere di primo grado ad un'incognita
Al contrario dell'equazioni, dove si verifica per quali valori vale una certa l'uguaglianza, nelle disequazioni occorre verificare per quali valori vale la disuguaglianza. Il principio con il quale si risolvono è molto simile a quello delle equazioni.
Un esempio di disequazione è il seguente
La prima differenza è che non viene più usato il segno =, ma i segni > (maggiore) e < (minore)
La soluzione si trova
risolvendo l'equazione associata, cioè 
, e dandone una interpretazione grafica.
La soluzione
dell'equazione associata è 
, per cui la disequazione è
riportiamo la soluzione su una linea retta sulla quale è rappresentato
l'insieme dei numeri reali (da 
a 
)
Poiché la disequazione è verificata per ogni numero maggiore di 4, si traccerà una linea continua a partire dal numero 4 a salire, mentre per i numeri minori di quattro si traccerà una linea tratteggiata per indicare che in quell'intervallo la disequazione non è verificata.
Particolare attenzione va prestata quando si cambia di segno alla disequazione: in questo caso cambia di segno anche il verso della disequazione (> diventa < e viceversa)
Es.
in questo caso occorre cambiare di segno per rendere la x positiva, facendo attenzione anche a cambiare il segno della disequazione.
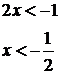
Disequazioni razionali intere di secondo grado ad un'incognita
Le disequazioni razionali intere di 2° grado assumono la forma
oppure 
Tralasciando la parte più complessa diamo solo il metodo di risoluzione.
Occorre risolvere l'equazione di 2° grado associata secondo la formula classica
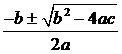che in genere
porta a due risultati differenti.
A questo punto occorre considerare il segno della a: se la a è positiva la disequazione è verificata per soluzioni esterne all'intervallo delimitato dalle due soluzioni, viceversa se la a è negativa le soluzioni saranno interne.
Es. 1 
risolviamo
l'equazione associata 
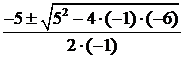
poiché
la a è negativa ( ), le
soluzioni sono interne all'intervallo e si scriverà così
cioè la
disequazione è verificata per x maggiore
di 2 e minore di 3
Es.
2 
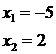
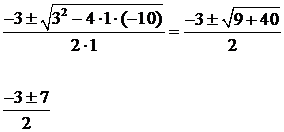
Es.
3 
questa disequazione
si risolve in modo diverso per trovare gli zeri dell'equazione, ma si procede
nello stesso modo per verificare la disuguaglianza.
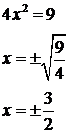
la a è positiva, quindi la disequazione è verificata per soluzioni esterne all'intervallo.
3/2
|
| Appunti su: |
|
| Appunti Fisica |  |
| Tesine Statistica |  |
| Lezioni Geografia |  |