 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2037 | Gradito: |
Leggi anche appunti:LA RAPPRESENTAZIONE della geometria di RiemannLA RAPPRESENTAZIONE della geometria di Riemann E' possibile ora porre la Insiemi numerici e progressioniINSIEMI NUMERICI E PROGRESSIONI La parola insieme è sinonimo di aggregato, L'elaborazione dei dati: i numeri indiciL'elaborazione dei dati: i numeri indici Numeri indici semplici Sono |
 |
 |
M A T E M A T I C A
Nella sezione dedicata alla Fisica abbiamo parlato della conduzione di corrente nelle soluzioni elettrolitiche. Ma la grandezza che caratterizza la corrente che scorre in un conduttore è l'intensità di corrente, ovvero la quantità di carica che attraversa una certa sezione di un conduttore nell'unità di tempo. Ma il rapporto tra intensità di corrente e quantità di carica può essere facilmente collegato nell'ambito matematico ai concetti di derivata e rapporto incrementale.
Le derivate
Se conosciamo la funzione q(t) che lega la quantità di carica al tempo, per ottenere l'intensità di corrente media relativa a una quantità di carica ∆q passata in un intervallo di tempo ∆t, calcoliamo:
![]()
dove im è il rapporto incrementale della quantità di carica considerata come funzione del tempo.
Passando al limite del rapporto incrementale al tendere a zero dell'incremento ∆t, ossia calcolando la derivata della finzione q(t), otteniamo, se il limite esiste, l'intensità della corrente che circola nel conduttore all'istante t:
![]()
Ora analizziamo meglio i concetti di rapporto incrementale e derivata.
La derivata di una funzione
Uno dei problemi classici che portarono
al concetto di derivata è quello della determinazione della retta tangente a
una curva in un punto. Per ogni conica è vero che la tangente in un punto P
interseca la conica stessa soltanto in P. Ma ci sono casi in cui la retta
tangente alla curva nel punto P la interseca anche nel punto P'. Per ottenere
una definizione valida in generale, ci si richiama al concetto di limite,
pensando al procedimento per cui si può approssimare meglio la tangente
mediante secanti. Così la definizione di retta
tangente a una curva diventa: La
retta tangente t a una curva in un 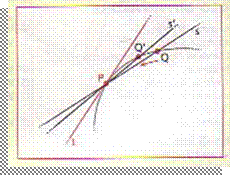 punto P è
la posizione limite, se esiste, della secante PQ al tendere( sia da destra che
da sinistra) di Q a P.
punto P è
la posizione limite, se esiste, della secante PQ al tendere( sia da destra che
da sinistra) di Q a P.
 Ora data la funzione
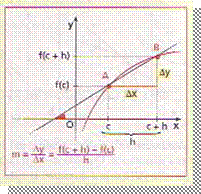
Ora data la funzione ![]() , definita in un
intervallo [a; b], e un punto del suo
grafico A(c; f(c)), le coordinate del
punto B del grafico di f, la cui
ascissa è data dalla somma di h con
l'ascissa di A, sono: xb = c+h ; yb = f(c+h) ossia
B(c+h; f(c+h)). Consideriamo gli
incrementi ∆x = xb - xa = h e ∆y = yb - ya = f(c+h) - f(c). Considerando il rapporto dei due incrementi si può
dare la definizione di rapporto
incrementale: Data una funzione
, definita in un
intervallo [a; b], e un punto del suo
grafico A(c; f(c)), le coordinate del
punto B del grafico di f, la cui
ascissa è data dalla somma di h con
l'ascissa di A, sono: xb = c+h ; yb = f(c+h) ossia
B(c+h; f(c+h)). Consideriamo gli
incrementi ∆x = xb - xa = h e ∆y = yb - ya = f(c+h) - f(c). Considerando il rapporto dei due incrementi si può
dare la definizione di rapporto
incrementale: Data una funzione ![]() , definita in un
intervallo [a; b], e due numeri reali c e c+h interni all'intervallo, si chiama
rapporto incrementale di f (relativo a c) il numero:
, definita in un
intervallo [a; b], e due numeri reali c e c+h interni all'intervallo, si chiama
rapporto incrementale di f (relativo a c) il numero:
![]()
Considerati i punti A e B del grafico di f, il rapporto incrementale di f relativo a c è il coefficiente angolare della retta passante per A e per B.
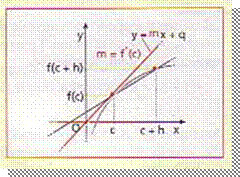 Attribuendo ad h valori
sempre più piccoli, il punto B si avvicina sempre di più al punto A. Quando h → 0 il punto B tende a
sovrapporsi al punto A e la retta AB tende a diventare la retta tangente alla
curva in A. Di conseguenza il coefficiente angolare della secante AB, ossia il
rapporto incrementale, tende al coefficiente angolare della tangente, che viene
chiamato derivata della funzione nel
punto c e di cui possiamo ora dare
una definizione: Data una funzione
Attribuendo ad h valori
sempre più piccoli, il punto B si avvicina sempre di più al punto A. Quando h → 0 il punto B tende a
sovrapporsi al punto A e la retta AB tende a diventare la retta tangente alla
curva in A. Di conseguenza il coefficiente angolare della secante AB, ossia il
rapporto incrementale, tende al coefficiente angolare della tangente, che viene
chiamato derivata della funzione nel
punto c e di cui possiamo ora dare
una definizione: Data una funzione ![]() , definita in un
intervallo [a; b], si chiama derivata della funzione nel punto c interno
all'intervallo il limite, se esiste ed è finito, per h che tende a 0, del
rapporto incrementale di f relativo a c e si indica con
, definita in un
intervallo [a; b], si chiama derivata della funzione nel punto c interno
all'intervallo il limite, se esiste ed è finito, per h che tende a 0, del
rapporto incrementale di f relativo a c e si indica con ![]()
![]()
La derivata di una funzione in un punto c rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c.
Così come per i limiti, possiamo definire per le derivate una derivata sinistra e una derivata destra di una funzione:
La derivata sinistra di una funzione
in un punto c è: 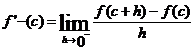
La derivata destra di una funzione in
un punto c è: 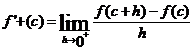
Una funzione è derivabile in un punto c se esistono finite e uguali tra loro la derivata sinistra e la derivata destra. Inoltre si può dire che: Una funzione y = f(x) è derivabile in un intervallo chiuso [a; b] se è derivabile in tutti i punti interni all'intervallo e se esistono e sono finite in a la derivata destra e in b la derivata sinistra.
Inoltre si può dire anche che se una funzione f(x) è derivabile nel punto x0 , in quel punto la funzione è anche continua. (di ciò è possibile fornire una dimostrazione). Non è vero il contrario, ovvero non è detto che se una funzione è continua in un punto x0 , allora in quel punto è anche derivabile.
Data una derivata ![]() è possibile calcolarne
a sua volta la derivata. A tale derivata daremo il nome di derivata seconda della funzione
è possibile calcolarne
a sua volta la derivata. A tale derivata daremo il nome di derivata seconda della funzione ![]() . Anche la derivata seconda è una funzione che possiamo
derivare; derivando quest'ultima otterremo la derivata terza. In generale, data
una funzione
. Anche la derivata seconda è una funzione che possiamo
derivare; derivando quest'ultima otterremo la derivata terza. In generale, data
una funzione ![]() , con il procedimento
esaminato si possono ottenere le derivata seconda, terza, quarta. Esse si
dicono derivate di ordine superiore della funzione data. La derivata di ordine
n di una funzione
, con il procedimento
esaminato si possono ottenere le derivata seconda, terza, quarta. Esse si
dicono derivate di ordine superiore della funzione data. La derivata di ordine
n di una funzione ![]() si indica con il simbolo
si indica con il simbolo ![]() .
.
 |
| Appunti su: derivata dell27intensitC3A0 di corrente, |
|
| Appunti Statistica |  |
| Tesine Geografia |  |
| Lezioni Fisica |  |