 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1573 | Gradito: |
Leggi anche appunti:GeometriaGEOMETRIA DEFINIZIONE GEOMETRICA Ripartizione di un segmento in due Risoluzione di una equazione differenziale del primo ordineRISOLUZIONE DI UNA EQUAZIONE DIFFERENZIALE DEL PRIMO ORDINE Il numero d'oro nella Successione di FibonacciIl numero d'oro nella Successione di Fibonacci Un uomo mise una coppia di conigli |
 |
 |
Consideriamo due funzioni reali f e g entrambe
infinitesime o entrambe infinite in un punto![]() . In tal caso il loro rapporto f/g si presenta in forma
indeterminata
. In tal caso il loro rapporto f/g si presenta in forma
indeterminata ![]() o
o ![]() perché il limite può
esistere (finito o infinito) come può non esistere. Un metodo utile per
studiare tali forme indeterminate è fornito dal seguente teorema
perché il limite può
esistere (finito o infinito) come può non esistere. Un metodo utile per
studiare tali forme indeterminate è fornito dal seguente teorema
TEOREMA DI L'HOPITAL(senza dimostrazione)
Siano f(x) e g(x) due funzioni reali
derivabili nell'intervallo ![]() con
con ![]() (nell'intervallo
(nell'intervallo ![]() con
con ![]() ). Supponiamo che risulti
). Supponiamo che risulti
![]()
E che i rapporti f/g e f'/g' abbiano
significato in ![]() (in
(in ![]() ) cioè che risulti
) cioè che risulti ![]()
![]() , se f e g sono infinitesime in
, se f e g sono infinitesime in ![]() . In tale ipotesi vale l'implicazione:
. In tale ipotesi vale l'implicazione:
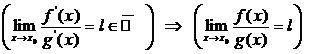
Osservazione 1 (notevole)
In base al teorema di l' Hospital ogni volta che il limite
![]()
Si presente nella forma indeterminata 0/0 o
nella forma ![]() si può cercare di
calcolare tale limite sfruttando il limite in
si può cercare di
calcolare tale limite sfruttando il limite in ![]() del rapporto delle
derivate
del rapporto delle
derivate
![]() .
.
Se quest' ultimo limite esiste (finito o
infinito) allora esiste anche il ![]() e risulta
e risulta
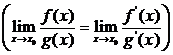 .
.
Naturalmente può capitare che anche il limite
in ![]() del rapporto delle
derivate f'/g' si presenti in forma indeterminata. In tal caso, se f' e g'
verificano le ipotesi del teorema di l' Hopital, è possibile riapplicare la
regola di l'Hopital e cioè si può provare a calcolare il limite
del rapporto delle
derivate f'/g' si presenti in forma indeterminata. In tal caso, se f' e g'
verificano le ipotesi del teorema di l' Hopital, è possibile riapplicare la
regola di l'Hopital e cioè si può provare a calcolare il limite ![]()
Evidentemente, se questo limite esiste, risulta
![]()
E conseguentemente
![]() .
.
Osservazione 2
Si noti che l'implicazione contenuta nel teorema di l' Hospital non si inverte. Consideriamo ad esempio le funzioni
![]()
Le quali sono entrambe infinitesime in 0 e verificano le ipotesi del teorema. Si ha
![]()
E quindi ![]() Tuttavia risulta:
Tuttavia risulta:
![]()
Osservazione 3
Da questi esempi si deduce che la regole di l'
Hospital si può applicare non solo ai limiti nelle forme indeterminate 0/0 e ![]() ma anche, con
opportuni artifici di calcolo, a tutte le forme indeterminate.
ma anche, con
opportuni artifici di calcolo, a tutte le forme indeterminate.
 |
| Appunti su: |
|
| Appunti Statistica |  |
| Tesine Fisica |  |
| Lezioni Contabilita |  |