 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 5755 | Gradito: |
Leggi anche appunti:Analisi vettorialeAnalisi vettoriale Insiemi di livello: disegnare l'insieme di livello Intervalli e intorniIntervalli e intorni Considerato che esiste una corrispondenza biunivoca che Il numero d'oro e la sezione aureaIL NUMERO D'ORO E LA SEZIONE AUREA Dal punto di vista della Matematica, a |
 |
 |
Introduzione
La serie di eventi e di
trasformazioni che hanno caratterizzato la storia di fine Ottocento è
accompagnata da un notevole progresso nel campo delle scienze. Le discussioni
filosofiche nate di fronte ad una società in costante evoluzione, soprattutto
dal punto di vista economico, tecnologico e sociale, portarono alla
ridefinizione degli stessi fondamenti della filosofia e delle scienze stesse.
Già verso la metà del secolo, con la formulazione di nuove geometrie non
euclidee, si incominciò a dubitare dell'assolutezza della Geometria (da sempre
considerata come modello fondamentale di scientificità e razionalità), e quindi
dello stesso concetto di matematica e del suo ruolo nelle altri campi
scientifici. Ma non è solo la pura matematica che incominciò a incontrare gravi
difficoltà nel trovare il proprio fondamento: anche i modelli della fisica da
sempre considerati come universalmente validi cominciarono a cadere e a non
essere più sufficienti come modelli esplicativi. Questi movimenti portarono alla
crisi del positivismo e l'inizio di una nuova Era dove le vecchie certezze vennero
sradicate e grazie a nuove scoperte si proposero nuovi modelli interpretativi
del mondo e dell'universo.
Il positivismo aveva stabilito nell'ambito della ricerca scientifica due punti fondamentali:
Tra la fine dell' '800 e l'inizio del '900 iniziarono però a sorgere dubbi fondamentali sulla validità dei modelli positivistici e vennero poste domande come:
La scienza può superare i suoi limiti metodologici? È davvero possibile, cioè, per un ricercatore soggettivo arrivare all'oggettività dei fatti? I linguaggi matematici sono davvero in grado di definire la verità e l'effettiva realtà delle cose? La scienza ha una natura convenzionale?
La crisi del positivismo nelle scienze è molto più evidente quando ci avviciniamo all'importante rivoluzione teoretica della fisica e della matematica, la quale coincide con la crisi della meccanica classica, le novità introdotte dalla fisica quantistica e il sorgere di geometrie non euclidee. La nuova analisi critica si richiama a questi principali punti:
Queste nuove problematiche portarono a rivalutare profondamente il concetto di tempo ma soprattutto il concetto di spazio. La matematica abbandonò le proprie certezze basate su una classica geometria euclidea e si propose nuovi modelli basati sull'operato di autorevoli scienziati tra i quali Einstein e Riemann.
L'idea di una quarta dimensione (spaziale o temporale) inizia però a svilupparsi già durante la seconda metà dell'ottocento e la sua diffusione sarà necessaria e propedeutica per la successiva formulazione della teoria della relatività di Albert Einstein. Uno tra i primi racconti che ha aperto l'immaginario collettivo al pensiero di un universo costituito da dimensioni superiori alla terza è Flatlandia. L'autore, Edwin Abbot, un monaco inglese, ci porta attraverso ciò che egli stesso definisce come un racconto fantastico a più dimensioni. Il testo è diviso in due parti. La prima fornisce una descrizione dettagliata su come esseri bidimensionali trascorrino la loro vita su una superficie piana ignari dell'esistenza di un'altra dimensione (l'altezza) a loro sconosciuta.
Flatlandia è un mondo abitato quindi da sole figure piane le quali hanno una capacità visiva che si orienta solo all'interno del piano stesso senza possibilità di <guardare> nella terza dimensione. Ogni essere vivente vedrà di conseguenza il proprio mondo come una linea retta, in quanto il proprio sguardo non può sollevarsi verso l'alto. Per chiarire: è come se poggiassimo fogli e righelli su un tavolo e li osservassimo ponendoci con lo sguardo sul bordo del tavolo stesso; i righelli e fogli ci apparirebbero così non più tridimensionali o bidimensionali (come se li osservassimo dall'alto) ma unidimensionali, vedremo infatti solo la loro lunghezza (escludendo però il minimo di spessore che possiedono). Per quanto assurda può sembrarci una vita presso un tale piano, Abbott ci mostra come esseri bidimensionali possano organizzarsi in maniera perfetta per il riconoscimento reciproco e per una pacifica convivenza. Tali esseri, seguendo il racconto di Abbot, sono suddivisi a livello sociale secondo il numero di lati che essi posseggono: minore sarà tale numero e minore sarà il proprio rango sociale (di conseguenza i cerchi, che possiamo considerare come poligoni aventi infiniti lati, apparterranno all'ordine superiore per eccellenza).
La limitata capacità visiva non permette loro di vedere l' "alto" e l'unico modo che (ad esempio) un quadrato ha di riconoscere un triangolo è quello di osservare come i suoi lati (che si sviluppano nella profondità del piano) vadano a sbiadirsi (in quanto essi tendono ad allontanarsi dall'osservatore), oppure può semplicemente tastare il triangolo stesso girandoci intorno.
Questa introduzione per quanto fantasiosa è fondamentale per comprendere che la nostra percezione di vivere in un mondo tridimensionale può essere una limitazione alla conoscenza della realtà. Le capacità (limitate) di ogni essere vivente (di qualsiasi dimensione) si adoperano affinché egli sviluppi una concezione solo dello spazio in cui vive e basi la sua intera esistenza secondo le possibilità che la sua dimensione gli offre.
E' interessante sottolineare che il monaco inglese nella descrizione precisa e metodica della vita bidimensionale mostri implicitamente una forte critica alla società vittoriana dell'800, basata su regole formali e sul materialismo che ostacolava ogni forma di immaginazione artistica e poetica. Il periodo nel quale il racconto fu scritto era infatti coincidente con l'evolversi del mondo vittoriano. Questo se da una parte portò a un notevole sviluppo industriale e tecnologico dall'altro fu motivo di ingiustizie e rivolte sociali dovute alle misere condizioni nelle quali venivano a trovarsi le classi più povere. Abbott mostra quindi, seppur in maniera velata, il suo disagio riguardo un mondo che aveva perso il suo spirito creativo. La stessa insofferenza è ravvisabile in altri autori contemporanei al monaco inglese come Charles Dickens il quale, tramite opere come Oliver Twist e Hard Times, critica fortemente la società vittoriana accusandola di aver abbandonato la componente irrazionale, fantasiosa e immaginativa che caratterizza l'uomo.
In Flatlandia si osserva come la società bidimensionale abbia reagito all'introduzione del colore (una forma di espressività artistica) nel proprio mondo ad opera di uno scienziato: repressione verso i seguaci del "colorismo" e messa al bando dello stesso scienziato. La società vittoriana si basava infatti su una serie di codici di valori formali che imponeva un certo meccanicismo alla vita del cittadino londinese reprimendo ogni forma di creatività.
La seconda
parte del racconto è la più interessante e fonte di maggiori spunti di riflessioni. Il viaggio che ci presenta Abbott è un viaggio
basato sull'analogia; egli aveva infatti
intuito che per spiegare al meglio l'esistenza di una quarta dimensione a un
essere tridimensionale quale siamo noi bisognasse presentare un essere tridimensionale
che tentasse di spiegare a un essere bidimensionale l'esistenza di una
dimensione superiore:
Immaginiamo ora però, seguendo il racconto di Flatlandia, non una sfera ma un quadrato. Questo assopitosi sogna un mondo unidimensionale, sogna cioè una retta. La visione che egli ha di tale mondo è un retta nella sua interezza in quanto egli può osservarla dall'esterno della retta stessa in quanto il quadrato non appartiene a tale mondo ma risulta spostato verso un'altra dimensione (egli infatti è come se vedesse la retta dall'alto).

Così come il suo mondo era popolato da esseri viventi allo stesso modo la retta è popolata da altri esseri (segmenti) unidimensionali (che io ho colorato per distinguerli tra loro),i quali si sviluppano quindi solo in lunghezza. La visione che ognuno di questi esseri ha del proprio mondo è semplicemente un punto; infatti è come se prendessimo un matita (intesa come una retta) e la osservassimo con la punta rivolta verso i nostri occhi: ciò che vedremmo non sarà la matita ma un punto.
Successivamente il quadrato parla.
Gli abitanti della retta ( che come gli abitanti del piano hanno sviluppato una propria civiltà efficiente nonostante siano limitati spazialmente rispetto alle dimensioni superiori) ascoltano una voce, ma non concepiscono da dove il suono arrivi (il suono infatti proviene da una dimensione che loro non possono osservare). Il quadrato tenta di spiegare la sua superiorità dimensionale al Re della retta ma questo (rispecchiando lo scetticismo umano verso il paranormale) chiede al quadrato di mostrarsi e di mostrare questa seconda dimensione nella quale egli vive. Il quadrato a questo punto per farsi osservare dal Re interseca la retta.
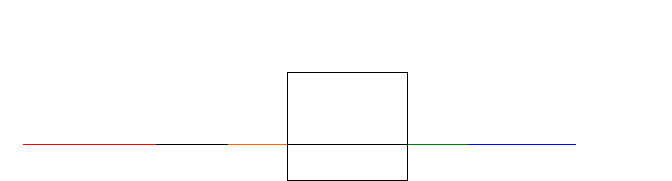
Ciò che però il Re vede non è altro che un punto, il quadrato infatti potrà manifestarsi in un mondo inferiore solo per sezioni del suo stesso corpo ( cioè per segmenti che visti dalla prospettiva del Re sembreranno sempre e comunque punti).
Un essere a n dimensioni potrà manifestare in un mondo a (n-1) dimensioni solo una sezione (n-1) dimensionale del suo stesso corpo. Ma lo scorrere del suo corpo presso tutto lo spazio inferiore mostrerà, seppur per sezioni, il proprio corpo dimensionalmente maggiore, potrà cioè mostrarsi nella sua completezza solo come somma di sezioni diverse del corpo nel tempo.
Inoltre il quadrato ha la facoltà di entrare e uscire dalla retta a suo piacimento, mostrando così al Re di essere in grado di spostarsi verso una dimensione superiore. Naturalmente tale Re come ogni essere umano rimane scettico all'apparizione di un essere superiore e si rifiuta di credere in questo essere che lui definisce come un illusionista imbroglione.
A questo punto il quadrato si sveglia.
Analogamente all'esperienza sognata dal quadrato sopraggiunge ora una sfera nel tentativo di spiegare al quadrato stesso l'esistenza di una terza dimensione.
Come si può immaginare il quadrato si trova nelle stesse difficoltà del Re nella comprensione di una dimensione superiore. Anch'egli infatti ascolta una voce ma non può vedere nella dimensione in cui si trova la sfera.
A questo punto anche la sfera, come aveva fatto il quadrato per la retta, interseca il piano bidimensionale.

![]()
![]() Anche in questo caso ciò che si
presenterà nel piano non sarà una sfera ma sezioni della sfera cioè circonferenze
di diverso raggio, a seconda di quanto la sfera sia "entrata" nel piano.
Dapprima il quadrato vedrà solo un punto (primo contatto tra la sfera e il
piano) successivamente vedrà dei segmenti sempre più grandi ( che comunque sarà
in grado di identificare come cerchi) fino a che la sfera si troverà
intersecata con il piano con il suo cerchio massimo (come l'equatore per la
terra), dopo di che le circonferenze tenderanno a rimpicciolirsi fino a che la
sfera non sarà uscita dall'altra parte del piano. Anche in questo caso il
quadrato si mostra scettico e chiede alla sfera di dargli una prova superiore
della sua effettiva tridimensionalità ( è interessante osservare come tali richieste riflettano
lo scetticismo umano nei confronti di ciò che la mente non può spiegare
razionalmente). Ora, immaginiamo la sfera al di sopra del piano. Ciò che
egli vede è TUTTO il mondo bidimensionale, è onniveggente (rispetto al
quadrato), può vedere tutto: ogni essere planare, l'interno delle case,
l'interno dei cassetti, l'interno dei mobili, l'interno del quadrato, conosce
tutto. A questo punto è facile capire come la sfera possa interagire con il
mondo inferiore a suo piacimento, tanto che può facilmente sottrarre un
gioiello del quadrato posto in una cassaforte e portarlo davanti al quadrato
stesso. Può infatti attraversare facilmente i muri e le limitazioni fisiche bidimensionali
in quanto egli proviene da una dimensione
superiore dalla quale il piano risulta aperto.
Anche in questo caso ciò che si
presenterà nel piano non sarà una sfera ma sezioni della sfera cioè circonferenze
di diverso raggio, a seconda di quanto la sfera sia "entrata" nel piano.
Dapprima il quadrato vedrà solo un punto (primo contatto tra la sfera e il
piano) successivamente vedrà dei segmenti sempre più grandi ( che comunque sarà
in grado di identificare come cerchi) fino a che la sfera si troverà
intersecata con il piano con il suo cerchio massimo (come l'equatore per la
terra), dopo di che le circonferenze tenderanno a rimpicciolirsi fino a che la
sfera non sarà uscita dall'altra parte del piano. Anche in questo caso il
quadrato si mostra scettico e chiede alla sfera di dargli una prova superiore
della sua effettiva tridimensionalità ( è interessante osservare come tali richieste riflettano
lo scetticismo umano nei confronti di ciò che la mente non può spiegare
razionalmente). Ora, immaginiamo la sfera al di sopra del piano. Ciò che
egli vede è TUTTO il mondo bidimensionale, è onniveggente (rispetto al
quadrato), può vedere tutto: ogni essere planare, l'interno delle case,
l'interno dei cassetti, l'interno dei mobili, l'interno del quadrato, conosce
tutto. A questo punto è facile capire come la sfera possa interagire con il
mondo inferiore a suo piacimento, tanto che può facilmente sottrarre un
gioiello del quadrato posto in una cassaforte e portarlo davanti al quadrato
stesso. Può infatti attraversare facilmente i muri e le limitazioni fisiche bidimensionali
in quanto egli proviene da una dimensione
superiore dalla quale il piano risulta aperto.
Se indaghiamo per un momento il racconto evangelico ci accorgeremo che ciò che è in grado di compiere la sfera può essere rapportato ad alcune azioni di Gesù. Egli infatti oltre a compiere una serie di miracoli ( i quali assumono una razionalità se inseriti nel discorso della quarta dimensione) è in grado di oltrepassare muri senza alcuna difficoltà come riporta Giovanni (20,19-31): "La sera di quello stesso giorno, il primo dopo il sabato, mentre erano chiuse le porte del luogo dove si trovavano i discepoli per timore dei giudei, venne Gesù, si fermò in mezzo a loro e disse."
Torniamo però al racconto di Abbot. La sfera ha dato prova di una sua superiorità dimensionale ma tuttavia il quadrato ancora non crede, e reputa l'essere tridimensionale oltre che un illusionista imbroglione anche un ladro. Alla sfera non resta che "spingere" dall'alto il quadrato verso il "basso" (2 direzioni della dimensione sconosciuta al quadrato stesso).
Il quadrato è trascinato fuori dal suo mondo e si muove ora anche nella terza dimensione. D'ora in poi egli vedrà il suo spazio come mai lo aveva visto: lo vedrà dall'alto, vedrà tutto il mondo come realmente è, avrà la facoltà di vedere, sentire, e interagire (se vuole) con ogni essere planare.
È facile capire come il quadrato consideri la sfera un Dio onnisciente, onniveggente e onnipotente rispetto al suo mondo, e in effetti così è. Conscio quindi dell'esistenza effettiva di una terza dimensione è intenzionato a ridiscendere nel piano e annunciare la RIVELAZIONE di un mondo superiore. Prima di ciò però la sfera decide di portare il quadrato ad osservare un mondo a-dimensionale.
Il mondo tridimensionale è definito dallo spazio solido, il mondo bidimensionale è definito dal piano, il mondo unidimensionale è costituito da una retta e infine il mondo a-dimensionale sarà definito da 1 solo punto
Questo punto
non vede nel suo universo che se stesso; egli è l'universo, non c'è nient'altro
al di fuori di sé . La sfera ora invita
il quadrato a mostrare al punto che in realtà esistono ben altre 3 dimensioni
oltre alla sua. Il quadrato parla. Il punto ascolta una voce ma questa volta
egli non chiede spiegazioni sull'origine di tale suono, il punto si crede "il
tutto" e si impersonifica anche con
Abbandonato il Punto, il quadrato pone infine un' importante richiesta al suo Dio-sfera: Egli gli ha mostrato il mondo tridimensionale, è bene che ora lo porti nel mondo quadrimensionale.
Paradossalmente la sfera nega irritata l'esistenza di una dimensione superiore alla sua e riporta il quadrato nel suo mondo bidimensionale.(A questo punto è bene osservare come anche coloro che vengono ritenuti grandi maestri rimangono chiusi nelle loro idee credendo di insegnare l'unica verità e conoscenza, rifiutando qualsiasi altra possibilità di realtà).
Tornato nel proprio mondo il quadrato inizia a narrare la sua esperienza al popolo. Non viene creduto, viene trattato come un eretico, un pazzo e viene lasciato morire in carcere.
Anche in questo caso è facile osservare una notevole somiglianza tra il messia cristiano e in questo caso il quadrato.
Ciò che Gesù si proponeva era di rivelare a noi esseri inferiori l'esistenza di un mondo diverso, di un mondo superiore e per dimostrare ciò ha compiuto una serie di azioni che non possono essere spiegate razionalmente se ci limitiamo a pensare lo spazio solo nelle sue 3 componenti spaziali. La Sua rivelazione non è stata però da tutti accettata ed egli fu crocifisso così come il quadrato fu costretto a morire rinchiuso in carcere.
Riflessioni
 Il racconto di Flatlandia sottolinea
come l'uomo sia abituato a vedere il mondo come esso gli si presenti e come
talvolta egli creda come unica realtà e verità ciò che le sue capacità
intellettive gli permettono di concepire. Già Platone nel "mito della caverna"
aveva intuito tale limitatezza umana. In esso si narra di esseri umani
costretti a vivere all'interno di una caverna con mani e piedi legati senza
alcuna possibilità di vedere nè i propri compagni nè loro stessi, con lo
sguardo indirizzato verso una parete. Immaginiamo poi che, appena fuori dalla
caverna, vi sia un muricciolo ad altezza d'uomo e che dietro questo, (quindi
interamente coperti dal muricciolo) si muovano degli uomini che portano sulle
spalle statue lavorate in pietra e in legno, raffiguranti tutti i generi di
cose.
Il racconto di Flatlandia sottolinea
come l'uomo sia abituato a vedere il mondo come esso gli si presenti e come
talvolta egli creda come unica realtà e verità ciò che le sue capacità
intellettive gli permettono di concepire. Già Platone nel "mito della caverna"
aveva intuito tale limitatezza umana. In esso si narra di esseri umani
costretti a vivere all'interno di una caverna con mani e piedi legati senza
alcuna possibilità di vedere nè i propri compagni nè loro stessi, con lo
sguardo indirizzato verso una parete. Immaginiamo poi che, appena fuori dalla
caverna, vi sia un muricciolo ad altezza d'uomo e che dietro questo, (quindi
interamente coperti dal muricciolo) si muovano degli uomini che portano sulle
spalle statue lavorate in pietra e in legno, raffiguranti tutti i generi di
cose.
Immaginiamo, ancora, che dietro questi uomini arda un grande fuoco e che, in
alto, splenda il sole. Infine immaginiamo che la caverna abbia una eco e che
gli uomini che passano al di là del muro parlino e che le loro voci rimbalzino
per effetto dell'eco. Ebbene, se così fosse, quei prigionieri non potrebbero
vedere altro che le ombre delle statue che si proiettano sul fondo della
caverna e udirebbero l'eco delle voci; ma essi crederebbero anche che le voci
dell'eco siano le voci prodotte da quelle ombre. Ora, supponiamo che uno di
questi prigionieri riesca a sciogliersi a fatica dai ceppi; ebbene, costui con
fatica riuscirebbe ad abituarsi alla nuova visione che gli apparirebbe e,
abituandosi, vedrebbe le statuette muoversi al di sopra del muro e capirebbe
che quelle sono ben più vere di quelle cose che prima vedeva e che ora gli
appaiono come ombre.
Se leggiamo
tale mito in chiave moderna e dal punto di vista matematico possiamo
interpretare il mito nel seguente modo.Il prigioniero di Platone è stato portato idealmente da una dimensione spaziale
"n" a concepire una dimensione
spaziale "n+
Non vi è infatti motivo di pensare che la quarta dimensione non sia anch'essa spaziale.
La cosa che più mi preme sottolineare è infatti che non è corretto indicare essa come una dimensione meramente temporale. Questa iperdimensione infatti è una dimensione spaziale a tutti gli effetti e si sviluppa secondo un piano esterno al mondo tridimensionale. Il tempo è possiamo dire una conseguenza della presenza di una dimensione superiore, esso ci permette di intuire ogni evento che si sviluppa nel tempo come uno spostamento del piano 3d all'interno di uno spazio 4d.
Lo scorrere del tempo è da noi percepito come una variazione di eventi. Se non ci fosse movimento, se nessun corpo (compreso il sole) si muovesse nello spazio allora saremmo portati a pensare che il tempo non esisterebbe in quanto non saremmo in grado di definire un prima o un dopo poiché non ci sarebbe alcun evento cui far riferimento. Potremmo al massimo calcolare il tempo come variazione dei nostri sentimenti, dei nostri stati d'animo, di ciò che William James chiamava "flusso di coscienza", ma in quel caso parleremmo di un tempo interiore e soggettivo e quindi non generalizzabile a ogni essere vivente. Dal momento che un certo evento accade noi siamo in grado di definirne il tempo passato in base ad altri fatti che ad esso sono seguiti ( è evidente infatti che se un evento accadesse in un mondo immobile e dopo di esso non accadesse nient'altro non potremmo mai dire il tempo che è passato dal manifestarsi dell'evento stesso). Il tempo trascorso rimane in ogni caso nella nostra memoria.
Esso sarà da noi ricordato non tanto in termini temporali quanto in termini spaziali: se pensiamo al passato infatti il ricordo sarà dato dallo spazio, ricorderemo immagini, situazioni, ricorderemo cioè uno spazio che è passato.Possiamo immaginare quindi il mondo quadrimensionale come un infinità di istanti dello spazio tridimensionale. Lo spazio 3d si muove all'interno dello spazio 4d e muta le sue caratteristiche; tale mutazione è da noi esseri umani convenzionalmente identificata come tempo.
La quarta dimensione è quindi una dimensione spaziale che sarà di conseguenza indicata da 4 coordinate. Un piano cartesiano permette di individuare figure piane mediante l'utilizzo di 2 cordinate (x,y) le quale identificano un punto secondo due direzioni dello spazio tra loro perpendicolari (rappresentazione 2d). Per poter rappresentare un oggetto solido ricorriamo invece in genere ad una assonometria (che può essere di diverso genere: cavaliera,
assonometria..) la quale oltre a presentare i due assi x,y ne presenta un altro che partendo dall'origine degli assi si sviluppa perpendicolarmente rispetto al piano in cui giacciono i due assi stessi. Per identificare un punto si utilizzeranno 3 coordinate (x,y,z). Ora la rappresentazione di un punto nella quarta dimensione avverrà per mezzo di 4 coordinate. La quarta direzione però non è rappresentabile a partire dalla assonometria poiché essa è limitata alle tre dimensioni spaziali nelle quale viviamo. Possiamo però immaginare tale nuovo asse come un asse esterno allo spazio 3d e pertanto sviluppatosi fuori dello spazio stesso. Immaginiamo il nostro spazio 3d come se fosse in realtà uno spazio bidimensionale disegnato su un foglio. La quarta dimensione è data da ciò che è l'altezza per il mondo bidimensionale. È una dimensione esterna al mondo 3d ma nella quale esso è immerso e lo spostamento del
mondo 3d all'interno dello spazio quadrimensionale si manifesta nello spazio 3d come lo scorrere del tempo.
Diverse sono le ipotesi e le teorie che tentano di dare una risposta alla questione tempo e una di esse è la seguente.
Cerchiamo di interpretare il tempo alla luce di queste nuove considerazioni. Immaginiamo di vivere in un mondo bidimensionale e che naturalmente il tempo non esista (in quanto abbiamo detto essere una coordinata spaziale). Se un essere di tale piano si spostasse da un punto ad un altro noi lo vedremmo nello stesso istante in due punti diversi. Ciò però non avviene. Osserviamo sempre e comunque lo stesso corpo in due punti diversi e distinti.
Ora immaginiamo che tale piano sia immerso in una dimensione spaziale superiore e che si muovi verso una determinata direzione ( per comodità intendiamo che si sposti verso destra). Basterà a questo punto mostrare come tale spostamento del piano nello spazio tridimensionale sia identificato dagli esseri bidimensionali con il tempo.
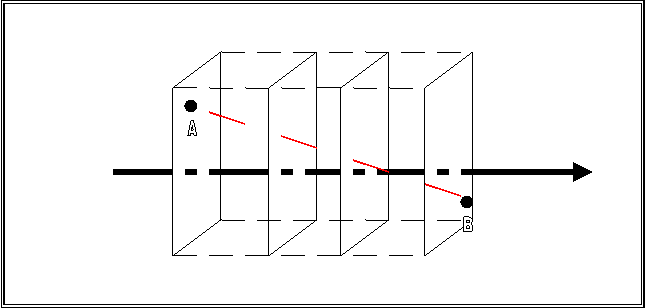 Se il piano si
sposta veramente in tale direzione allora osserveremo un essere che si muove da
un punto ad un altro non più contemporaneamente nei due punti ma prima in uno e
poi in un altro. Questo perché l'essere occupa due punti di due piani distinti.
Il piano infatti spostandosi lascia dietro di se varie superfici che se sommate
danno luogo allo spazio tridimensionale.
Se il piano si
sposta veramente in tale direzione allora osserveremo un essere che si muove da
un punto ad un altro non più contemporaneamente nei due punti ma prima in uno e
poi in un altro. Questo perché l'essere occupa due punti di due piani distinti.
Il piano infatti spostandosi lascia dietro di se varie superfici che se sommate
danno luogo allo spazio tridimensionale.
Seguendo tale modello ( che prevede il movimento unidirezionale di un mondo all'interno di una dimensione superiore) è facile intuire come lo spostamento lungo l'asse orizzontale sia identificato come il tempo. Il passato sarà dato dal ricordo dei piani precedenti mentre il futuro sarà dato dai piani che si verranno a creare. Interessante è notare che nonostante si viva sulla superficie bidimensionale è possibile spostarsi lungo la terza coordinata (rimanendo addirittura fermi, poiché è lo spazio stesso che si muove dandoci l'illusione del tempo).
Ci chiediamo quindi: se un abitante del piano volesse "vedere" un oggetto tridimensionale, ad esempio una sfera che intersechi il piano, cosa può fare? La risposta è che egli dovrà semplicemente immaginare di mettere una sopra all'altra tutte le infinite fettine della sfera che vede mentre la attraversa (utilizzando la propria memoria).
La sfera prenderà vita nella sua testa solo quando riuscirà a immaginarsi un corpo esteso anche lungo l'asse orizzontale, che viva cioè contemporaneamente nel suo passato nel suo presente e nel suo futuro.
A questo punto aggiungiamo una dimensione cercando di interpretare il nostro mondo.
Se, quando vediamo una persona muoversi, vediamo sempre istante per istante un'unica persona e non la vediamo mai in due posti contemporaneamente è perché il nostro universo tridimensionale è in realtà immerso in un mondo a quattro dimensioni spaziali e, supponendo che il nostro universo tridimensionale si stia spostando lungo un determinato asse , otteniamo le stesse conseguenze che vengono dal pensare che esista il tempo.
In questo modo si osserva che non c'è alcuna necessità di considerare il tempo come una coordinata di natura diversa dalle prime tre coordinate spaziali.
(L'unica differenza fondamentale dalle altre 3 coordinate è che il tempo non è reversibile. Se misuriamo un segmento la misura vale sia che prendiamo un punto A come inizio e un punto B come fine che viceversa. Per quante riguarda distanze "temporali" tale principio non vale).
Il nostro mondo è quindi in ogni istante un'infinitesima fettina dello spazio quadridimensionale e tutto lo spazio quadridimensionale è formato da tutti gli infiniti universi tridimensionali corrispondenti ad ogni istante.
E' interessante notare come tutto questo ragionamento si sposi perfettamente con la figura del Dio cristiano onniscente e la teoria del libero arbitrio. Supponiamo infatti che Dio esista e che sia un essere n-dimensionale (n>3) e supponiamo che dalla conoscenza dell'universo a un certo istante possa essere dedotto lo svolgimento di ogni azione futura (determinismo newtoniano). Questo vuol dire che Egli potrà osservare dall'esterno tutto l'universo quadridimensionale nel quale noi siamo immersi. In questa posizione Dio si troverà davanti a sé contemporaneamente tutti gli infiniti universi tridimensionali corrispondenti a tutti gli istanti, cioè avrà dispiegato davanti a sé passato, presente e futuro del nostro universo tridimensionale. Infatti poiché il tempo universale lo consideriamo fermo, tutti gli infiniti spazi tridimensionali che noi non vediamo più (perché sono "passati") rimangono lì dove sono e tutti insieme concorrono a formare tutto lo spazio quadridimensionale. Ecco spiegato il motivo per cui Dio è onnisciente. Inoltre si capisce che Dio sappia prevedere il futuro e contemporaneamente lasci agli uomini la libertà di scegliere cosa fare (almeno ci lascia l'illusione di poterlo fare). Può inoltre però intervenire e operare apparizioni 3d e compiere quelli che a noi appaiono miracoli ma che possono essere compresi se si estende il pensiero alla quarta dimensione. Anche quelle apparizioni di spiriti o fantasmi, una volta accertata la loro autenticità., possono essere spiegati come l'intersezione tra un essere quadrimensionale e il nostro spazio tridimensionale
Come immaginare e rappresentare un oggetto quadrimensionale
Ora dopo aver dato una possibile e probabile ipotesi di come sia fondato in realtà lo spazio cerchiamo di capire come sia possibile rappresentare un oggetto 4d.
Per poter immaginare tale oggetto si è accennato alla capacità di farlo mediante la ricostruzione e la sovrapposizione nel tempo di sezioni 3d dell'oggetto stesso. A tale risultato si può arrivare facilmente per analogia. Ricordiamo inoltre che abbiamo inteso noi stessi come se fossimo sezioni 3d immersi in uno spazio 4d. Ora immaginiamo un quadrato che si muove nello spazio 3d. Esso rimarrà sempre 2d ma si sposterà nello spazio 3d. Ora se sommiamo ogni spostamento del quadrato nello spazio 3d (ovvero se sommiamo ogni sua sezione che si crea dal movimento del quadrato 2d nell'universo 3d) otteniamo un solido (intendiamo per semplicità un cubo). Per il quadrato la costruzione del cubo sarà data dalla somma di "se stesso" nel tempo.
![]()
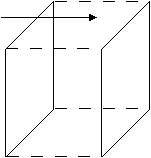
Possiamo ottenere lo stesso effetto velocizzando con il nostro intervento il movimento del quadrato: se costruiamo un quadrato di legno e lo muoviamo velocemente a destra e a sinistra si osserverà la costruzione di un cubo ( per la persistenza di immagini sulla retina). Non bisogna quindi sommare sezioni dell'oggetto (quadrato) nel suo stesso piano (altrimenti avremmo un quadrato più grosso e nient'altro) ma la sovrapposizione va immaginata nella dimensione superiore.
Un oggetto 3d è solo una sezione di un oggetto 4d che si manifesta nelle sue sezioni 3d al variare del "tempo".
La somma mentale di tale sezioni porta a immaginare l'oggetto quadrimensionale.
Nella pratica è possibile però operare in un ulteriore modo.
La costruzione che facciamo è analoga a quella che si compie per ricostruire un solido a partire da una proiezione ortogonale.
In questa infatti riportiamo su un piano 2d un oggetto 3d ma scomposto secondo le sue facce. Per immaginarlo solido e reale immaginiamo di chiudere le facce proiettate in modo perpendicolare al piano e quindi chiuderle nella terza dimensione.
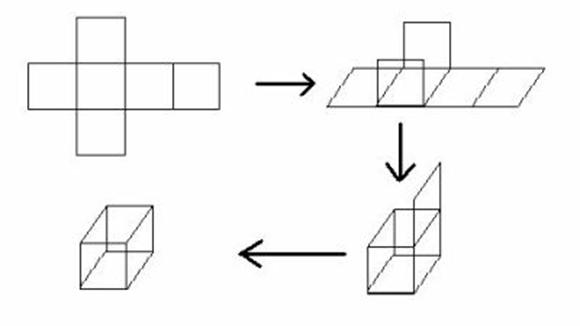
Le facce del solido saranno quindi le facce della proiezione.
Analogamente le facce di un oggetto quadrimensionale saranno date dalle facce di questo oggetto proiettate nello spazio 3d, pertanto esse non saranno piane ma solide.
Da questo possiamo dedurre che possiamo immaginare un oggetto 4d studiando le sue diverse proiezioni 3d
Più proiezioni osserviamo (da vari punti di vista) più informazioni abbiamo sull'oggetto che si estende all'esterno del nostro spazio. Sommando nel tempo le proiezioni e ricombinandole possiamo avere un idea dell'oggetto.
Se immaginiamo un cubo che varia la sua forma nel tempo (secondo regole precise) in realtà stiamo osservando le varie componenti tridimensionali di un oggetto (ipercubo) chiuso nello spazio superiore (4d).
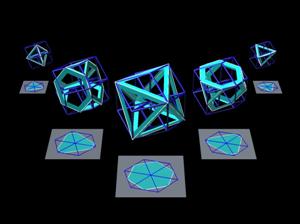

E' difficile pensare che gli oggetti solidi in figura tanto differenti tra loro siano in realtà parte dello stesso oggetto quadrimensionale, eppure è così.
Una ipersfera d'altra parte sarà data dallo somma di infinite sfere di diversa grandezza.
Immaginiamo, ad esempio, un palloncino che si gonfia e poi si sgonfia, vedremo prima un punto e poi delle sfere che progressivamente diventeranno sempre più grosse e che, ad un certo punto, cominceranno a rimpicciolire fino a che di esse non resterà che un punto. La somma mentale delle infinite dimensioni che ha assunto il palloncino al variare del tempo indica l'ipersfera.
L'ipersfera non sarà quindi altro che la somma in uno spazio quadrimensionale di diverse sfere 3d. Immaginiamo infatti che una ipersfera intersechi il nostro piano 3d. inizialmente vedremo un punto poi una sfera che aumenterà sempre le proprie dimensioni (fino a una grandezza massima) dopodichè tenderà a rimpicciolirsi fino a svanire nel nulla (cioè nella 4 dim.). A questo punto avremmo osservato varie sezione 3d di un essere 4d che se ricomposte portano mentalmente all'ipersfera.

Dante e la quarta dimensione
È interessante notare che se analizziamo la struttura dei cieli del paradiso dantesco esso sarà strutturato proprio secondo un'ipersfera.
Il Paradiso dantesco mostra un universo tolemaico con una rigida struttura geometrica, che vede la Terra al centro di una serie di nove sfere concentriche crescenti, rappresentanti i cieli della Luna, di Mercurio, di Venere, del Sole, di Marte, di Giove, di Saturno, delle Stelle Fisse, e del Primo Mobile o Cristallino. Quest'ultimo, che «non ha altro dove che la mente divina» (XXVII, 109-110), racchiude l'universo sensibile e ne è al di fuori allo stesso tempo.
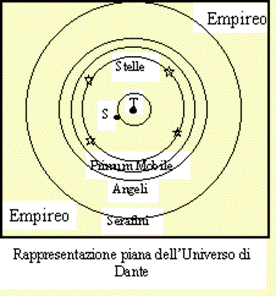 Oltre il Primo Mobile vi
è il cielo empireo, raffigurato come una simmetrica serie di nove sfere
concentriche decrescenti, che sono le sedi di Angeli, Arcangeli, Principati,
Potestà, Virtù, Dominazioni, Troni, Cherubini e Serafini, e il cui centro è un
punto di luce abbagliante che rappresenta Dio: «un punto vidi che raggiava lume
acuto sì, che'l viso ch'elli affoca chiuder conviensi per lo forte acume» (XXVIII, 16-18).
Oltre il Primo Mobile vi
è il cielo empireo, raffigurato come una simmetrica serie di nove sfere
concentriche decrescenti, che sono le sedi di Angeli, Arcangeli, Principati,
Potestà, Virtù, Dominazioni, Troni, Cherubini e Serafini, e il cui centro è un
punto di luce abbagliante che rappresenta Dio: «un punto vidi che raggiava lume
acuto sì, che'l viso ch'elli affoca chiuder conviensi per lo forte acume» (XXVIII, 16-18).
 L'universo
dantesco si compone dunque di due serie di sfere distinte, una sensibile e
l'altra celeste, i cui centri sono rispettivamente la Terra e Dio. Dante (XXVIII,
46-57) è inoltre turbato da una mancanza di simmetria: le sfere dell'universo sensibile sono infatti tanto più perfette quanto
più si allontanano dal centro terrestre, mentre quelle dell'universo celeste
diventano tanto più perfette quanto si avvicinano al centro divino. Inoltre
risulta dalla descrizione che il cielo celeste come già detto comprenda al suo
interno la sfera sensibile pur essendo distinta da essa.
L'universo
dantesco si compone dunque di due serie di sfere distinte, una sensibile e
l'altra celeste, i cui centri sono rispettivamente la Terra e Dio. Dante (XXVIII,
46-57) è inoltre turbato da una mancanza di simmetria: le sfere dell'universo sensibile sono infatti tanto più perfette quanto
più si allontanano dal centro terrestre, mentre quelle dell'universo celeste
diventano tanto più perfette quanto si avvicinano al centro divino. Inoltre
risulta dalla descrizione che il cielo celeste come già detto comprenda al suo
interno la sfera sensibile pur essendo distinta da essa.
Per capire cosa succeda nel divino universo dantesco è utile ragionare per analogia prendendo a modello il globo terrestre.
Se si potesse vedere l'emisfero meridionale dal polo sud, l'immagine che se ne avrebbe sarebbe quella di una serie di cerchi concentrici (i paralleli), che si ingrandiscono fino a raggiungere un massimo (l'equatore). Recandosi all'equatore e guardando l'emisfero settentrionale, si vedrebbe una situazione opposta: una serie di cerchi concentrici che diminuiscono, fino a raggiungere un punto (il polo nord). La Terra si può dunque effettivamente rappresentare mediante due serie di cerchi, che si devono immaginare come aventi la circonferenza dell'equatore in comune.
L'universo dantesco non è che una rappresentazione
analoga: i cerchi concentrici diventano sfere concentriche, le coincidenti
circonferenze dei cerchi massimi diventano le coincidenti superfici delle sfere
massime, e la sfera che rappresenta la Terra diventa una ipersfera che
rappresenta l'universo. Rimane da chiarire che cosa volesse dire Beatrice
nella sua spiegazione a Dante riguarda l'apparente a-simmetria tra i cieli
celesti quelli sensibili, e come sia possibile che Dio appaia «inchiuso da quel
ch'elli 'nchiude» (XXX, 12). Anche qui basterà considerare il globo terrestre:
se esso fosse un fiore con lo stelo nel polo sud, ad esempio una «candida rosa»
(XXXI, 1), al suo dispiegarsi i paralleli 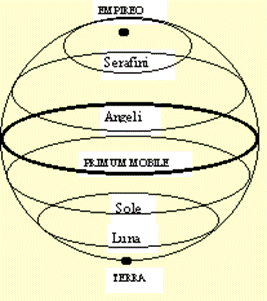 diventerebbero cerchi via via più
grandi, man mano che si avvicinano al polo nord. E il polo stesso diventerebbe
non solo un intero cerchio, ma il più grande di tutti.
diventerebbero cerchi via via più
grandi, man mano che si avvicinano al polo nord. E il polo stesso diventerebbe
non solo un intero cerchio, ma il più grande di tutti.
Analogamente, se l'ipersfera dantesca potesse dispiegarsi nello spazio a quattro dimensioni, il punto divino diventerebbe una sfera che racchiuderebbe tutte le altre.
Relatività e curvatura dello spazio
 Notevole influsso inoltre ebbe l'idea
della quarta dimensione nella teoria einsteniana della relatività (specialmente
riguardo la relatività generale del 1915). Il fisico tedesco riprendendo anche
l'operato del maestro Minkowski e seguendo anche i modelli matematici di Riemann
aveva ipotizzati l'esistenza di uno spazio-tempo 4-dimensionale. Ipotesi che
sarà poi verificata a seguito di esperimenti successivi. Einstein riteneva che
il tempo fosse fortemente legato allo spazio e ai corpi e che quindi non fosse
un dato oggettivo distinto dalle masse ma che venisse alterato da queste in
determinate condizioni. Egli sosteneva che una massa potesse incurvare lo
spazio nel quale era immerso come una pallina incurva un cuscino. Naturalmente
tale incurvatura doveva essere esterna alle 3 dimensioni. Infatti se ho un
foglio (piatto e quindi bidimensionale) per incurvarlo dovrò piegarlo verso
l'alto, muovendomi quindi verso una dimensione superiore; allo stesso modo per incurvare
lo spazio tridimensionale mi muoverò verso una dimensione esterna. Tale
curvatura è data, secondo la relatività, dalla presenza di masse nello spazio.
Essa è causa dell'effetto gravitazionale. Una biglia posta in prossimità di un
cuscino incurvato dal peso di una sfera più pesante infatti sarà da essa
attratta come se ci fosse una forza (gravitazionale) intrinseca alla massa.
Notevole influsso inoltre ebbe l'idea
della quarta dimensione nella teoria einsteniana della relatività (specialmente
riguardo la relatività generale del 1915). Il fisico tedesco riprendendo anche
l'operato del maestro Minkowski e seguendo anche i modelli matematici di Riemann
aveva ipotizzati l'esistenza di uno spazio-tempo 4-dimensionale. Ipotesi che
sarà poi verificata a seguito di esperimenti successivi. Einstein riteneva che
il tempo fosse fortemente legato allo spazio e ai corpi e che quindi non fosse
un dato oggettivo distinto dalle masse ma che venisse alterato da queste in
determinate condizioni. Egli sosteneva che una massa potesse incurvare lo
spazio nel quale era immerso come una pallina incurva un cuscino. Naturalmente
tale incurvatura doveva essere esterna alle 3 dimensioni. Infatti se ho un
foglio (piatto e quindi bidimensionale) per incurvarlo dovrò piegarlo verso
l'alto, muovendomi quindi verso una dimensione superiore; allo stesso modo per incurvare
lo spazio tridimensionale mi muoverò verso una dimensione esterna. Tale
curvatura è data, secondo la relatività, dalla presenza di masse nello spazio.
Essa è causa dell'effetto gravitazionale. Una biglia posta in prossimità di un
cuscino incurvato dal peso di una sfera più pesante infatti sarà da essa
attratta come se ci fosse una forza (gravitazionale) intrinseca alla massa.
In realtà non è la massa che attrae ma è la modificazione dello spazio (prodotto da questa) che produce un vortice attrattivo. Naturalmente tanto più sarà pesante il corpo e tanto più la deformazione spazio-tempo sarà rilevante.
La curvatura dello spazio a livello matematico non è spiegabile a partire dalla geometria euclidea. Essa infatti è valida per interpretare lo spazio su piccola scala, il quale può essere considerato per approssimazione piatto. La nostra terra ad esempio è sferica ma se consideriamo una porzione relativamente piccola della superficie allora potremmo considerarla piatta. In generale se prendiamo una porzione sufficientemente piccola di uno spazio curvo qualunque, possiamo sempre considerare in esso lo spazio come 'quasi' perfettamente piatto, euclideo. Su larga scala però la geometria euclidea non risulta più valida.
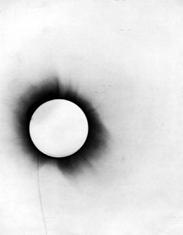 La curvatura dell'universo ha trovato
nel corso del secolo notevoli conferme. La prima, poi rivelatasi impropria, si
ebbe nel 1919, quando osservazioni di Arthur Eddington durante un'eclisse di Sole
confermarono la visibilità di alcune stelle vicine al bordo solare, che in
realtà avrebbero dovuto essere invisibili: i fotoni luminosi venivano deviati
dal Sole della quantità prevista dalle equazioni. In realtà, le osservazioni
avevano un errore medio dello stesso ordine di grandezza dell'effetto
considerato.
La curvatura dell'universo ha trovato
nel corso del secolo notevoli conferme. La prima, poi rivelatasi impropria, si
ebbe nel 1919, quando osservazioni di Arthur Eddington durante un'eclisse di Sole
confermarono la visibilità di alcune stelle vicine al bordo solare, che in
realtà avrebbero dovuto essere invisibili: i fotoni luminosi venivano deviati
dal Sole della quantità prevista dalle equazioni. In realtà, le osservazioni
avevano un errore medio dello stesso ordine di grandezza dell'effetto
considerato.
La prima vera conferma fu la spiegazione del moto di precessione del perielio di Mercurio,
inspiegabile con
 Un'altra conferma più recente, ma
ormai completamente accettata dalla comunità scientifica, è l'effetto lente gravitazionale
di cui le osservazioni di Eddington sono un caso particolare. La luce emessa da
una sorgente lontana, transitando nelle vicinanze di un oggetto molto massiccio
può venire deviata, con un effetto complessivo che può sdoppiare (o meglio
trasformare in un anello), l'immagine della sorgente.
Un'altra conferma più recente, ma
ormai completamente accettata dalla comunità scientifica, è l'effetto lente gravitazionale
di cui le osservazioni di Eddington sono un caso particolare. La luce emessa da
una sorgente lontana, transitando nelle vicinanze di un oggetto molto massiccio
può venire deviata, con un effetto complessivo che può sdoppiare (o meglio
trasformare in un anello), l'immagine della sorgente.
.Il fatto che il campo gravitazionale creato dalle masse incurvi lo spazio-tempo produce conseguenze assolutamente nuove rispetto alla meccanica classica. Esse possono essere riassunte nelle seguenti
spostamento
verso il rosso (red shift) gravitazionale. A
causa dell'incurvamento dello spazio-tempo un orologio immerso in un campo
gravitazionale viene visto marciare più lentamente da un osservatore
posizionato al di fuori del campo (ovvero dove il campo è più debole).
Supponiamo allora di osservare un orologio posto sulla superficie del sole dove
il campo gravitazionale è sicuramente molto intenso. Secondo quanto
precedentemente affermato lo dovremmo vedere segnare il tempo più lentamente di
un analogo orologio posizionato qui sulla terra. Il problema è che non potremo
mai posizionare un orologio sul sole per via della enorme temperatura. Possiamo
però utilizzare gli 'orologi naturali' che già vi sono posizionati.
Gli atomi eccitati emettono radiazioni di frequenza ben determinata. Noi
possiamo considerare queste frequenze tipiche di ogni atomo come degli orologi
perfetti. Osservando le frequenze di emissione degli atomi sul sole osserviamo che
esse ci appaiono minori, più rosse, di quello che dovrebbero essere e ciò conformemente
all'incurvamento dello spazio-tempo prodotto dal campo gravitazionale solare.
2- spostamento del perielio di Mercurio. Mercurio è il pianeta più vicino al sole e
la sua orbita deve risentire più di ogni altro pianeta dell' incurvamento
spaziale generato dal campo gravitazionale solare. Gia da metà '800
era nota una piccola variazione (43' per secolo) del perielio di mercurio
secondo la quale il pianeta non percorre una ellisse chiusa, bensì compie un'orbita
a 'rosetta'. Questa anomalia non trovava una spiegazione
nell'ambito della teoria newtoniana. All'interno della Relatività Generale
questo fenomeno trova una spiegazione nell'incurvamento spaziale che in prossimità
del sole è apprezzabile.
3- deviazione della posizione apparente delle stelle nelle vicinanza della
superficie solare  Se lo spazio è incurvato dal campo
gravitazionale del sole, un raggio di luce che passa nelle sue vicinanze (dove
l'incurvamento è maggiore ed il fenomeno più rilevabile) non può compiere
un cammino rettilineo (come se lo spazio fosse euclideo). Le stelle
posizionate (apparentemente) nei pressi della superficie del sole
devono allora avere la loro luce deviata dal campo gravitazionale solare.
Il sole funge allora da 'lente gravitazionale' e le stelle appaiono
spostate rispetto alla posizione che hanno quando sono posizionate lontane
(apparentemente) dal sole. Questo fenomeno è verificabile solo durante le
eclissi solari totali.
Se lo spazio è incurvato dal campo
gravitazionale del sole, un raggio di luce che passa nelle sue vicinanze (dove
l'incurvamento è maggiore ed il fenomeno più rilevabile) non può compiere
un cammino rettilineo (come se lo spazio fosse euclideo). Le stelle
posizionate (apparentemente) nei pressi della superficie del sole
devono allora avere la loro luce deviata dal campo gravitazionale solare.
Il sole funge allora da 'lente gravitazionale' e le stelle appaiono
spostate rispetto alla posizione che hanno quando sono posizionate lontane
(apparentemente) dal sole. Questo fenomeno è verificabile solo durante le
eclissi solari totali.
4- buchi neri.
Se la massa di una
certa distribuzione di materia è sufficientemente grande e gli atomi
possono avvicinarsi liberamente, si ha il fenomeno del collasso gravitazionale.
Ciò può accadere in una  stella che sta esaurendo il
combustibile nucleare che la tiene in vita, (l'idrogeno). Quando una stella si
raffredda, essa comincia a contrarsi e a ridursi di volume fino
a densità enormi (col raffreddamento progressivo, la gravità, che è sempre
centripeta, vince la repulsione elettrica fra i protoni i quali
vengono compattati sempre più e combinati con
gli elettroni fino a che la stella diventa composta da soli
neutroni). Quando (se ciò è possibile) tutta la materia di un corpo
che collassa entra dentro la superficie degli eventi di quel corpo (ogni
corpo ha la propria, per la terra è una sfera di raggio
stella che sta esaurendo il
combustibile nucleare che la tiene in vita, (l'idrogeno). Quando una stella si
raffredda, essa comincia a contrarsi e a ridursi di volume fino
a densità enormi (col raffreddamento progressivo, la gravità, che è sempre
centripeta, vince la repulsione elettrica fra i protoni i quali
vengono compattati sempre più e combinati con
gli elettroni fino a che la stella diventa composta da soli
neutroni). Quando (se ciò è possibile) tutta la materia di un corpo
che collassa entra dentro la superficie degli eventi di quel corpo (ogni
corpo ha la propria, per la terra è una sfera di raggio
Evoluzione dell'universo.
L'equazione di Einstein è in grado di descrivere l'evoluzione sia del campo gravitazionale che del moto delle masse al suo interno. L'equazione di Einstein è in grado di spiegare, quindi, anche la struttura dell'universo nel suo insieme (in larga scala, ovvero quando i fenomeni quantistici che agiscono a livello atomico e subatomico sono ininfluenti).
Nel
1929 la scoperta (dovuta a Hubble) dello spostamento verso il rosso delle galassie
(red shift cosmologico) la cosmologia prese una direzione ben
precisa: l'universo sembra espandersi.
Osservando gli spettri delle galassie essi appaiono più rosse di quello che
dovrebbero essere. Ciò si può spiegare in base all'effetto Doppler. Questo
effetto, che noi sperimentiamo comunemente nel campo delle onde
acustiche (il fischio del treno che ci viene incontro è più alto mentre è più
basso quando si allontana), afferma che
la frequenza di un'onda i qualunque tipo (acustica, elettromagnetica) emessa da
una sorgente in moto relativo rispetto ad un osservatore appare maggiore
se la sorgente si muove in direzione ell'osservatore, minore se si
allontana.
Ora, se tali spettri appaiono spostati verso il rosso, ciò potrebbe significare
che le galassie si stanno allontanando rispetto a noi. L'universo, quindi, si starebbe
espandendo e, portando il processo all'indietro nel tempo, probabilmente,
in un lontano passato, esso doveva essere tutto concentrato in un
volume limitato da cui, poi, è iniziata l'espansione. Questa è
l'ipotesi del big bang che oggi rappresenta la teoria più
avvalorata sulle origini e l'evoluzione del cosmo.
Se l'universo si espande, ci possono essere due possibilità. O
l'espansione dura per sempre e l'universo è destinato a diventare sempre
più rarefatto e freddo oppure, dopo l'espansione, se la massa totale è
sufficientemente grande, l'universo comincerà ad implodere (big crunch)
fino a tornare alla situazione iniziale per poi, magari, esplodere nuovamente
e ricominciare ad espandersi di nuovo.
L'avverarsi di uno o l'altro dei modelli dipende dalla massa complessiva
dell'universo. La misura della massa totale è un problema assai complesso
perchè la massa di cui ci perviene 'informazione' è
solo quella che emette radiazione elettromagnetica (al momento noi
'vediamo' l'universo attraverso telescopi ottici,
radiotelescopi, telescopi a raggi infrarossi,
x ecc. ma tutti solo in grado di captare radiazioni elettromagnetiche).
Nell'universo, però, c'è sicuramente anche della massa della quale non ci
perviene informazione, la cosiddetta massa
oscura. E' formata almeno dai buchi
neri e dai neutrini, nel caso essi abbiano massa non nulla (non è
ancora chiaro se la massa del neutrino sia nulla o no).
Se consideriamo solo la massa visibile, sembra che essa sia troppo piccola per
contrapporsi all'espansione per cui l'universo dovrebbe espandersi per
sempre. Il problema è aperto ma, mentre si stanno facendo stime ed ipotesi
sempre più approfondite sulla massa oscura, una scoperta recente (ancora
in fase di verifica) è destinata a rivoluzionare tutte le nostre idee
riguardo
al cosmo : sembra che l'espansione dell'universo stia addirittura accelerando
(in positivo).
Lo spazio e il tempo secondo Kant.
L'analisi del concetto di spazio e di tempo è operata da Kant nella Critica della ragion pura. In essa il filosofo si interroga sui modi e sulle possibilità di conoscere dell'intelletto umano. È importante sottolineare che, secondo la filosofia kantiana, l'uomo non conosce le cose come esse sono di per sé ma le conosce solo in base alle proprie modalità di apprensione. L'uomo per tanto è limitato nella sua conoscenza dalle sue stesse possibilità. Kant afferma che il tempo e lo spazio siano due forme pure a priori dell' intuizioni. Lo spazio non è costituito dai fenomeni, ma questi si sviluppano e presentano tra loro rapporti e relazioni solo in quanto agenti all'interno di forme spaziali e temporali esistenti a priori. Lo spazio non può infatti essere conosciuto a posteriori dall'esperienza per esempio osservando due oggetti e la loro posizione reciproca in quanto già il poter stabilire una distanza tra loro presuppone l'esistenza dello spazio stesso. Lo spazio è quindi una intuizione appartenente al soggetto grazie alla quale ci è permessa una intuizione esterna. Se lo spazio è la forma secondo cui il soggetto avverte i fenomeni esterni, il tempo è la forma in cui il soggetto avverte le proprie modificazioni interne. Così il tempo non viene ricavato dall'esperienza ma è il fondamento interiore dell'animo che permette di definire se alcuni avvenimenti sono avvenuti simultaneamente o meno.
Riporto qui due estratti inerenti all'estetica trascendentale.
Che cos'è lo spazio?
Lo spazio non è altro
se non la forma di tutti i fenomeni dei sensi esterni, cioè la condizione
soggettiva l'unica per la quale ci è possibile un'intuizione esterna, della
sensibilità.
Lo spazio non è un concetto empirico, ricavato da esperienze
esterne. Infatti, affinché certe sensazioni vengano riferite a qualcosa fuor di
me (cioè a qualcosa in un luogo dello spazio diverso da quello in cui mi trovo
io) e affinché io possa rappresentarmele come esterne e accanto le
une alle altre, quindi non solo differenti ma anche in luoghi differenti, deve
esserci già a fondamento la rappresentazione dello spazio.
Kant Critica della ragion pura
Che cos'è il tempo? «Il tempo non è affatto un concetto empirico, che sia stato tratto da qualche esperienza. In effetti, la simultaneità o la successione non si presenterebbero neppure alla percezione, se come fondamento non si trovasse a priori la rappresentazione del tempo. Soltanto sotto questo presupposto, ci si può rappresentare, che un qualcosa sussista in un solo e medesimo tempo (simultaneamente) oppure in temi diversi (successivamente). Il tempo è una rappresentazione necessaria che sta a fondamento di tutte le intuizioni. [] Il tempo è dunque dato a priori. Soltanto in esso è possibile una qualsiasi realtà delle apparenze. [] Il tempo non è altro che la forma del senso interno, cioè dell'intuizione di noi stessi e del nostro stato interno. Infatti, il tempo non può essere una determinazione di fenomeni esterni: non appartiene né alla figura, né al luogo, ecc.; determina, al contrario, il rapporto delle rappresentazioni nel nostro stato interno. E appunto perché questa intuizione interna non ha nessuna figura, noi cerchiamo di supplire a questo difetto con analogie e rappresentiamo la serie temporale con una linea che si prolunghi all'infinito nella quale il molteplice forma una serie avente una sola dimensione; e dalle proprietà di questa linea argomentiamo tutte quelle del tempo, fuorché questa sola; che le parti della linea sono simultanee, laddove le parti del tempo sempre successive. Da ciò risulta che la rappresentazione del tempo stesso è una intuizione, poiché tutti i suoi rapporti possono essere espressi per mezzo di una intuizione esterna.
Kant Critica della ragion pura
Con la crisi del positivismo e l'introduzione di nuove geometrie il concetto di spazio e tempo come forme a priori tende a svanire. Kant infatti rimane fortemente legato alla geometria euclidea e ritiene essa come esempio strutturale sul quale mostrare l'efficienza di quei giudizi sintetici a priori. In realtà però come mostrarono in seguito matematici come Poincarè, Riemann e Lobachevsky tale geometria non è vera ma semplicemente coerente. Ciò porta quindi a pensare che siano possibili altre geometrie (che presentano sempre una coerenza di assiomi) utili alla descrizione e alla rappresentazione dello spazio. Kant impiega, per la formulazione dei concetti di «spazio e tempo», le definizioni della fisica classica, sebbene egli sostenga che tutte le «asserzioni generali» sul «tempo» e sullo «spazio» derivano dalle loro forme a priori. Il problema è che queste definizioni risultano non essere valide per alcuni campi della fisica, in quanto si rifanno apertamente - volente o nolente - alla matematica classica e alla geometrica euclidea, le quali non sembrano essere appropriate per lo studio dei nuovi eventi fisici. Per Einstein questa concezione ha dimenticato che in realtà la «geometria euclidea» è solamente una costruzione teorica, sebbene sia efficiente e chiara. Rispetto infatti alle geometrie ellittiche e iperboliche quella euclidea risulta la più semplice e chiara ma non per questo deve avere pretesa di veridicità. Infatti con l'introduzione di nuove geometrie (tutte valide per la descrizione del mondo fisico) non ha più alcun senso crederne una vera e le restanti inadeguate in quanto sono in conclusione delle pure forma convenzionali operate dall'intelletto umano. Lo spazio e il tempo non risultano più forme a priori ma pure convenzioni, la scelta delle quali è data semplicemente dalla chiarezza e dalla semplicità della geometria data.
Picasso era solito dire: "la natura è una cosa, la pittura un'altra". In questo modo egli pone in rilievo il fatto che la pittura non deve essere piegata dal realismo della natura, ma deve essere in grado di trascendere da essa e svilupparsi su un piano parallelo. La rappresentazione del vero è così rifiutata mentre viene elogiata un tipo di pittura che tende a distorcere le componenti spazio-temporali del mondo. È importante sottolineare che il sorgere delle avanguardie pittoriche del novecento coincida con lo sviluppo scientifico- matematico di nuove teorie fondanti il nostro universo. L'idea della ricerca di una quarta dimensione è quindi ripresa da tali artisti dalla ideologia intellettuale che viene sviluppandosi proprio in quel periodo.
La corrente più rappresentativa di tale ricerca è senza dubbio il cubismo. I maggior rappresentanti di tale movimento (Ricasso e Braque) non cercano di compiacere l'occhio umano imitando la realtà ma tentano di costruirne una nuova e diversa tipologia. La principale caratteristica del cubismo è la scomposizione degli oggetti in piani e forme geometriche elementari a cui segue una sinterizzazione di punti di vista diversi, i quali nella realtà non possono essere adottati simultaneamente. L'adozione di differenti prospettive contemporaneamente presuppone la capacità da parte dell'artista di muoversi nel tempo attorno all'oggetto della pittura. In questo modo egli sarà in grado di dipingere introducendo nell'opera anche la variabile temporale. La quarta dimensione infatti è in questo caso intesa non tanto come dimensione spaziale quanto strettamente temporale. È interessante notare come indirettamente ognuno di noi sia stato per un breve periodo una sorta di pittore cubista: la casa stilizzata disegnata da un bambino è infatti un esempio di arte cubista. Egli infatti è solito disegnare il lato della casa e l'entrata della stessa senza adottare alcuna prospettiva (altra caratteristica tipica del cubismo) ponendo le due componenti una di fianco all'altra.
 Il quadro che, convenzionalmente,
viene indicato come l'inizio del Cubismo è «Les demoiselles d'Avignon»,
realizzato da Picasso tra il 1906 e il 1907.
Il quadro che, convenzionalmente,
viene indicato come l'inizio del Cubismo è «Les demoiselles d'Avignon»,
realizzato da Picasso tra il 1906 e il 1907.
Il quadro non rappresenta un risultato definitivo: dopo aver effettuato diversi schizzi e aggiunte Picasso decise di smettere di lavorarci. Lo abbandona nel suo studio, e quasi per caso suscita la curiosità e l'interesse dei suoi amici uno dei quali, Andrè Salmon, attribuisce all'opera il titolo con cui oggi è conosciuta.
Il soggetto del quadro è la visione di una casa in cui figurano cinque donne. In origine doveva contenere anche due uomini, poi scomparsi nelle successive modifiche apportate al quadro da Picasso.
Le due figure centrali hanno un aspetto molto diverso dalle figure ai lati. In queste ultime, specie le due di destra, la modellazione dei volti ricorda le maschere africane che in quel periodo conoscevano un momento di grande popolarità tra gli artisti europei.
Ciò che costituisce la grande novità dell'opera è l'annullamento dello spazio inteso come contenitori di oggetti. In questo dipinto infatti non sono solo gli oggetti a risultare deformati ma è lo stesso spazio che interseca le sue componenti con gli oggetti e con se stesso. L'immagine si compone infatti di una serie di piani solidi che si intersecano secondo angolazioni diverse. Ogni angolazione è il frutto di una visione parziale per cui lo spazio si satura di materia annullando la separazione tra un corpo ed un altro.
Le singole figure, costruite secondo il criterio della visione simultanea da più lati, si presentano con un aspetto decisamente inconsueto che sembra ignorare qualsiasi legge anatomica. Vediamo così apparire su un volto frontale un naso di profilo, oppure, come nella figura in basso a destra, la testa appare ruotata sulle spalle di un angolo innaturale. Tutto ciò è comunque la premessa di quella grande svolta, che Picasso compie con il cubismo, per cui la rappresentazione tiene conto non solo di ciò che si vede in un solo istante, ma di tutta la percezione e conoscenza che l'artista ha del soggetto che rappresenta.
Bisogna ora però ricordare che la quarta dimensione ha affascinato anche artisti di altre correnti d'avanguardia. Tra questi vanno ricordati Umberto Boccioni, appartenente al movimento futurista, e Salvador Dalì più legato al surrealismo.
Il primo nonostante fosse uno dei padri fondatori del futurismo risultò fortemente influenzato dal cubismo. Ciò è infatti ravvisabile in una sua particolare opera: "la Risata" del 1911.

Il titolo dell'opera è dato dalla risata della signora dal cappello rosso posta in alto a sinistra. I fasci di luce portano all'interno del dipinto una carica di dinamicità ( elemento caro ai futuristi) e creano uno strano effetto di profondità. In questo modo la definizione di spazio prospettico viene meno in quanto esso risulta decomposto in una visione simultanea di corpi e oggetti fluttuanti nel vuoto e intersecati tra loro. Un elemento chiave che richiama il cubismo è poi il bicchiere di vino rosso il quale è presentato sia frontalmente che verticalmente fondendo così nello stesso tempo due punti di vista differenti.
Il secondo artista, Salvador Dalì, risulta anch'egli legato in qualche modo alla tematica della quarta dimensione in quanto uno dei suoi capolavori mostra infatti lo sviluppo di un ipercubo all'interno di un mondo tridimensionale, nel quale un essere superiore quale cristo viene crocifisso. L'opera ha come titolo 'Corpus Hypercubus' realizzata nel 1954.
 Il titolo della tela fa
riferimento al fatto che la figura di Cristo non è inchiodata all'usuale croce, ma è
magicamente sospesa nell'aria, accostata ad una struttura fatta da otto cubi
che simulano la forma della croce, ma che in realtà esprimono la
rappresentazione dello sviluppo, nello spazio tridimensionale, di un solido che
si studia nella geometria della 'quarta dimensione': l'ipercubo.
Il titolo della tela fa
riferimento al fatto che la figura di Cristo non è inchiodata all'usuale croce, ma è
magicamente sospesa nell'aria, accostata ad una struttura fatta da otto cubi
che simulano la forma della croce, ma che in realtà esprimono la
rappresentazione dello sviluppo, nello spazio tridimensionale, di un solido che
si studia nella geometria della 'quarta dimensione': l'ipercubo.
Si tratta di un solido (avente come 'facce' otto cubi) che non è
possibile vedere, essendoci preclusa la quarta dimensione, ma solo intuire.
L'analogia con lo sviluppo delle facce di cubo su di un piano, può aiutare però
a comprendere la raffigurazione.
 |
|
| Appunti Fisica |  |
| Tesine Statistica |  |
| Lezioni Contabilita |  |