 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3075 | Gradito: |
Leggi anche appunti:Sviluppo in serie di una funzioneSviluppo in serie di una funzione Si definisce sviluppo in serie di Estremo superiore e inferiore di un insieme numericoESTREMO SUPERIORE E INFERIORE DI UN INSIEME NUMERICO Definizione Le geometrie non euclideeLe geometrie non euclidee Il problema delle geometrie non euclidee e la rivoluzione |
 |
 |
La parabola
La definizione della parabola è la seguente: è il luogo di punti del piano equidistanti da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice non passante per il fuoco.
Tenendo conto a chi è rivolto questo lavoro, la definizione ha un'importanza relativa, ma era necessario introdurla per chiarire che ci sono dei punti particolari (fuoco, direttrice) che sono rappresentativi di ogni parabola
L'equazione della parabola è rappresentata da un espressione di secondo grado di questo tipo:
Equazione della parabola

![]()
Come al solito la x e la y sono incognite, mentre a, b e c sono valori numerari.
Fig. 1
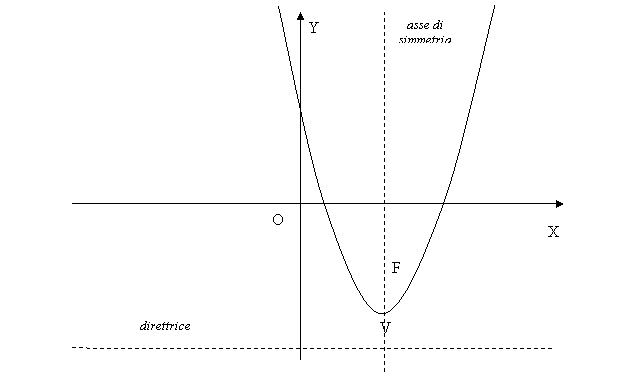
Il vertice è il punto più basso (nel caso in cui la concavità sia rivolta verso l'alto), l'asse di simmetria passa per il vertice ed è parallelo all'asse Y
Queste sono le formule degli elementi significativi
Vertice Fuoco
Fuoco 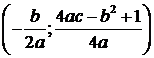
asse di
simmetria ![]() direttrice
direttrice 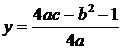
Per determinare l'equazione di una parabola sono necessarie tre condizioni, in quanto i parametri da trovare sono tre (a, b, c).
a) le coordinate di un punto della parabola danno una condizione;
b) le coordinate del vertice danno due condizioni ;
c) le coordinate del fuoco danno due condizioni;
d) l'equazione della direttrice da una condizione;
e) l'equazione dell'asse di simmetria da una condizione;
f) l'equazione di una retta tangente alla parabola da una condizione.
Equazione di una parabola passante per tre punti
Trovare l'equazione della parabola passante per A(0;-8), B(1;-10), C(2;-6)
L'equazione generica è ![]() . Si imposta un sistema a tre equazioni sostituendo alle x e
alla y i valori di ciascun punto.
. Si imposta un sistema a tre equazioni sostituendo alle x e
alla y i valori di ciascun punto.
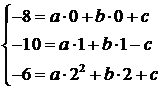

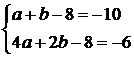
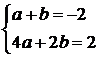


L'equazione finale sarà dunque ![]()
Calcolare il vertice della parabola
Troviamo il vertice della parabola dell'esempio precedente ![]()
Applicando la formula sarà:
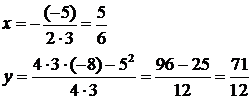
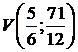
Se per trovare l'equazione della parabola viene dato il vertice, questo
rappresenta da solo 2 delle condizioni necessarie ponendo ad es. ![]() e
e 
Disegnare la parabola
La rappresentazione grafica della parabola richiede la determinazione di alcuni punti significativi sul sistema di assi cartesiano.
Il primo è vertice, punto più basso o più alto (a seconda di dove è rivolta la concavità della parabola), poi è consigliabile trovare le intersezioni con gli assi x ed y.
Es. Disegnare la seguente
parabola ![]()
Il vertice sarà
![]()
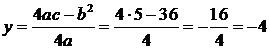
![]()
L'asse di simmetria, la cui equazione è uguale all'ascissa del vertice,
è ![]()
Per trovare le intersezioni con gli assi è necessario mettere a sistema l'equazione della parabola con quella di ogni asse cartesiano (ricordiamo: x=0 per l'asse delle y ed y=0 per l'asse delle x)
 La soluzione è
immediata in quanto sostituendo 0 alle x
resta
La soluzione è
immediata in quanto sostituendo 0 alle x
resta ![]()
che è l'intersezione della parabola con l'asse delle ordinate.
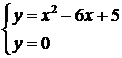
![]() risolviamo l'equazione
di 2° grado
risolviamo l'equazione
di 2° grado
![]()
![]()
![]()
![]()
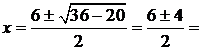 Queste
sono le intersezioni con l'asse x
Queste
sono le intersezioni con l'asse x

Equazione della retta tangente alla parabola in un punto dato
Questa in genere è una delle parti più complesse per i ragazzi. Ci si limiterà quindi a dare la formula e vederne l'applicazione.

![]() equazione della retta tangente alla parabola
in un punto
equazione della retta tangente alla parabola
in un punto
di coordinate P(X1;Y1)
Es.
![]()
![]()
Applicando la formula otteniamo
![]() ricordando che
nelle equazioni è possibile eliminare il denominatore calcolando il minimo
comune multiplo tra i termini del 1° e 2° membro
ricordando che
nelle equazioni è possibile eliminare il denominatore calcolando il minimo
comune multiplo tra i termini del 1° e 2° membro

Questa è l'equazione della retta tangente alla parabola data nel punto P.
Equazioni particolari della parabola
Se la b=0 la formula sarà del tipo ![]() questa parabola ha il
vertice tangente all'asse delle ascisse .
questa parabola ha il
vertice tangente all'asse delle ascisse .
Se la c=0 la formula sarà del tipo ![]() in questo caso la
parabola passa per l'origine O (0;0).
in questo caso la
parabola passa per l'origine O (0;0).
Se la b=0 e la c=0 la formula sarà del tipo ![]() la parabola ha il suo asse di simmetria che coincide con l'asse
delle ordinate e il vertice coincide con O(0;0)
la parabola ha il suo asse di simmetria che coincide con l'asse
delle ordinate e il vertice coincide con O(0;0)
Inoltre se la a è negativa la concavità volge verso il basso, se la a è positiva la concavità volge verso l'alto.
 |
| Appunti su: la parabola tesina matematica, https:wwwappuntimaniacomscientifichematematicala-parabola83php, download free software equazione di una parabola vertice e fuoco, |
|
| Appunti Contabilita |  |
| Tesine Geografia |  |
| Lezioni Statistica |  |