 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1416 | Gradito: |
Leggi anche appunti:La matematica oltre il numero - tesinaISTITUTO TECNICO INDUSTRIALE "LEONARDO DA VINCI" Indirizzo "SCIENTIFICO TECNOLOGICO" LA Serie di funzioniSERIE DI FUNZIONI DEFINIZIONE Si definisce serie di funzione una serie La risoluzione delle equazioni di 1° gradoLa risoluzione delle equazioni di 1° grado Consideriamo la seguente uguaglianza: |
 |
 |
Definizione 1
Sia ![]() e
e ![]() . Si dice che
. Si dice che ![]() è il limite di
è il limite di ![]() in
in ![]() o anche che
o anche che ![]() converge ad
converge ad ![]() in
in ![]() o anche che
o anche che ![]() tende a
tende a ![]() al tendere di
al tendere di ![]() a
a ![]() e si scrive:
e si scrive:
![]()
Quando ![]() verifica la seguente
proprietà:
verifica la seguente
proprietà:
(#) ![]()
![]()
![]() e
e ![]()
![]()
![]()
Osservazione
Analogamente a quanto visto per le successioni, essendo:
![]()
![]()
La definizione di limite espressa dalla proprietà (#) è equivalente a:
![]()
![]()
![]()
Osservazione 1
Dalle definizioni di limite si deduce che all'esistenza del limite l concorrono soltanto i valori assoluti
di f
in punti contenuti in un opportuno intorno ![]() di
di ![]() e diversi da
e diversi da ![]() .
.
Analogamente il limite l
di f
in ![]() è un numero che può esistere anche quando non esiste il
valore f(
è un numero che può esistere anche quando non esiste il
valore f(![]() ) di f in
) di f in ![]() (ciò è possibile perché il punto
(ciò è possibile perché il punto ![]() non è tenuto ad appartenere ad A). Inoltre all'esistenza del
limite l concorrono soltanto i valori
di f
che sono contenuti in un intervallo I(
non è tenuto ad appartenere ad A). Inoltre all'esistenza del
limite l concorrono soltanto i valori
di f
che sono contenuti in un intervallo I(![]() ) di
) di ![]() (carattere locale della definizione di limite).
(carattere locale della definizione di limite).
Definizione 2
Sia ![]() e
e ![]() . Si dice che
. Si dice che ![]() è il limite di f
in
è il limite di f
in ![]() o anche che f in
o anche che f in
![]() diverge positivamente
o anche che f tende a
diverge positivamente
o anche che f tende a ![]() per x che tende a
per x che tende a ![]() e si scrive
e si scrive
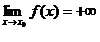
Quando f verifica la seguente proprietà:
(#)![]()
![]()
![]() e
e ![]()
![]() .
.
Osservazione 2
Assunto che:
![]()
La proprietà (#) che fornisce la definizione di limite nel caso considerato, è equivalente alla seguente:
![]()
![]()
![]()
Definizione 3
Sia f(x) una funzione reale definita in un insieme ![]() non limitato
superiormente sicché
non limitato
superiormente sicché ![]() è punto di accumulazione per A.
è punto di accumulazione per A.
Si dice che il numero ![]() è il limite di f(x) per
è il limite di f(x) per
![]() o anche che f(x) converge
ad l per
o anche che f(x) converge
ad l per ![]() e si scrive
e si scrive
![]()
Quando f verifica la seguente proprietà
(#)![]()
![]()
![]() e
e ![]()
Analogamente a quanto visto per le predente definizioni di limite, tale proprietà è equivalente alla seguente che restituisce gli intorni delle disuguaglianze
![]()
![]()
![]()
Osservazione 4
Si noti che, in particolare, la precedente definizione di limite (#)
restituisce la definizione di limite per le successioni ![]() nel caso delle
convergenti.
nel caso delle
convergenti.
Osservazione 5
In maniera del tutto analoga, lasciamo allo studente che si definiscano i simboli di limite:
![]() ;
; ![]() ;
; ![]() .
.
Determiniamo qualche considerazione sulla definizione di limite per le funzioni osservando che, analogamente a quanto detto per le successioni, le varie definizioni di limite si possono riassumere tutte nell'unica:
Definizione generale di limite
Sia ![]() ,
, ![]() un punto di
accumulazione per A (al finito o anche all'infinito). Denotiamo col simbolo
un punto di
accumulazione per A (al finito o anche all'infinito). Denotiamo col simbolo ![]() un intorno qualsiasi di
un intorno qualsiasi di
![]() e con
e con ![]() un intorno qualsiasi di
un intorno qualsiasi di ![]() .
.
Vale la seguente equivalenza:
![]()
![]()
![]()
![]()
![]()
![]()
Inoltre, analogamente a quanto fatto per le successioni si dice che una
funzione f è regolare nel punto ![]() quando è dotata di limite in
quando è dotata di limite in ![]() , si dice che f è non regolare in
, si dice che f è non regolare in ![]() quando non è dotata di
limite in
quando non è dotata di
limite in ![]() .
.
Esempi:
(semplici sulla verifica di un limite da pag.
 |
| Appunti su: |
|
| Appunti Fisica |  |
| Tesine Statistica |  |
| Lezioni Geografia |  |