 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1328 | Gradito: |
Leggi anche appunti:Modulazione fmMODULAZIONE FM Generalità La modulazione di frequenza si ottiene variando Elementi di propulsione a vaporeElementi di propulsione a vapore A metà circa del XIX Sec. compare un nuovo tipo Diagramma causa-effettoDiagramma causa-effetto Il pensiero scientifico si basa essenzialmente |
 |
 |
LA RELATIVITA' RISTRETTA e LA RELATIVITA' GENERALE
"I concetti che tu hai creato guidano ancora oggi il nostro modo di pensare, sebbene ora noi sappiamo che essi dovranno essere sostituiti da altri più lontani dalla sfera dell'esperienza immediata, se vogliamo aspirare a una profonda comprensione delle leggi della fisica." Einstein, rivolto idealmente a Newton
Nel 1905 Albert Einstein pubblica sulla rivista Annalen der Physik un articolo intitolato "Elettrodinamica dei corpi in movimento": era l'inizio della teoria sulla relatività ristretta.
La relatività affonda le sue radici nel relativismo classico, e si pone come raccordo delle osservazioni operate dagli scienziati del '900. Infatti essa si compendia di due postulati.
Primo postulato
Le leggi secondo cui variano gli stati di un sistema fisico non dipendono dal fatto di essere riferite all'uno o all'altro di due sistemi di coordinate in moto relativo uniforme.
Secondo postulato
Un raggio di luce si muove in ogni sistema inerziale di coordinate con la stessa velocità c , sia se venga emesso da una sorgente fissa o da una sorgente in movimento.
Il primo è il principio relativistico galileiano esteso a tutte le leggi della fisica; si reinterpretano le teorie di Maxwell per i corpi stazionari estendendole a quelli in movimento: i fenomeni elettromagnetici non possiedono proprietà corrispondenti all'idea di quiete assoluta. Il secondo assume che la velocità della luce (nel vuoto) sia costante per qualunque osservatore. Se infatti la velocità della luce non fosse una costante universale, le equazioni di Maxwell dell'elettromagnetismo non potrebbero avere la stessa forma rispetto a tutti i sistemi di riferimento inerziali. Inoltre, in contraddizione con il primo postulato, misurare la velocità della luce sarebbe un mezzo per distinguere l'uno dall'altro i diversi sistemi.
" Prima si credeva che, se ogni cosa dovesse improvvisamente sparire dal nostro mondo, rimarrebbero comunque lo spazio e il tempo. Dopo la relatività speciale e quella generale sono convinto che insieme a ogni cosa dovranno sparire anche lo spazio e il tempo"
Risultava comunque difficile capire come la luce avesse la stessa velocità per un osservatore che si avvicini a essa o che le si allontani. I due postulati richiedono l'abbandono della concezione di spazio e tempo fondata su un'idea di continuum spaziale che fluisce attraverso un continuum temporale, e comporta l'assunzione di un continuum spazio-temporale in cui distanze ed intervalli variano al mutare del sistema di riferimento; il tempo quindi diverrà una quarta dimensione.
oggetto fermo
oggetto con
velocità costante c t
![]() I diagrammi spazio-tempo. Il
cronotopo
I diagrammi spazio-tempo. Il
cronotopo
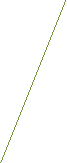
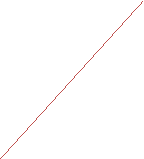 lo spazio-tempo implica che le posizioni in cui si
lo spazio-tempo implica che le posizioni in cui si
verificano gli eventi giacciano lungo una stessa
retta. Sull'asse delle ascisse si riporta la coordinata
spaziale x e sull'asse delle ordinate il rapporto della
velocità della luce c per il tempo t.
raggio di luce
Le linee tracciate sono dette linee
di universo: con
cui si rappresentano i vari eventi (nascita di un
x
bambino, esplosione stellare).
![]() Se un oggetto è
fermo, la sua linea di universo
Se un oggetto è
fermo, la sua linea di universo
è una retta verticale, parallela all'asse del tempo:
mentre il tempo scorre, la coordinata spaziale
non varia. Notiamo invece che per la luce la linea è inclinata di un angolo maggiore
corrisponderebbe ad una velocità maggiore di c.
Il concetto di simultaneità
"Supponiamo di affermare che quel treno arriva alle ore sette: questa affermazione significa che la sovrapposizione della lancetta piccola dell'orologio con il numero sette e l'arrivo del treno presso l'orologio sono due eventi simultanei"
La sincronizzazione degli orologi
Nella frase sopra riportata, Einstein si riferiva però alla simultaneità tra eventi che accadono nello stesso luogo. Nel caso in cui occorra confrontare correttamente i tempi in cui si verificano due eventi che accadono in due luoghi diversi, bisogna utilizzare due orologi sincronizzati e tecnologicamente uguali, uno posizionato nel punto in cui accade il primo evento, l'altro nel punto in cui accade il secondo.
Un processo di sincronizzazione può essere effettuato inviando a due osservatori posti vicino agli orologi un segnale che viaggi nello spazio il più velocemente possibile. Poiché finora non è stata scoperta una metodologia di comunicazione più rapida delle onde elettromagnetiche, poniamo esattamente nel punto di mezzo della congiungente i due orologi, una sorgente di onde, scelte, per esempio, nel campo delle radiazioni luminose che, come sappiamo, viaggiano sempre alla stessa velocità in qualsiasi direzione. Nel momento in cui arriva il segnale messo dalla sorgente, ogni osservatore potrà regolare il proprio orologio esattamente al tempo t=0. Questa tecnica permette di sincronizzare due orologi, reciprocamente fermi, e tra loro distanti.
Una volta sincronizzati gli orologi, posizionati nei due sistemi di riferimento, possiamo affermare che due eventi che accadono in luoghi diversi sono simultanei se i corrispettivi orologi associati agli eventi registrano la stessa ora.
La simultaneità è relativa
Tutto cambia se i due orologi non sono fermi, ma sono in moto reciproco e localizzati in diversi sistemi di riferimento inerziali.
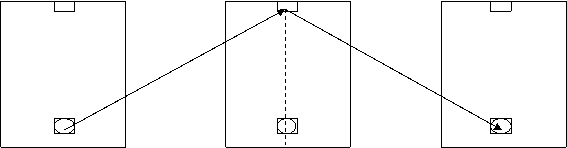
Un uomo si trova al buio al centro di un lungo vagone di un treno in moto con velocità costante. A un certo istante, utilizzando un'apposita sorgente, l'uomo invia due pennelli luminosi diretti verso le due estremità del vagone, sulle cui pareti si trovano dei dispositivi in grado di segnalare l'arrivo della radiazione luminosa. Poiché la velocità della luce è costante, l'onda raggiungerà i due dispositivi segnalatori nello stesso intervallo di tempo. Per l'osservatore posto all'interno del vagone i due eventi, "luce che raggiunge la testa" e "luce che raggiunge la coda" avvengono simultaneamente. L'osservatore, che a terra, col proprio orologio, vede passare il treno, osserva che la luce si muove con velocità costante in entrambe le direzioni; però nota che, nel valutare la stessa sequenza di eventi, mentre la parete superiore si avvicina verso la luce, quella anteriore si allontana da essa. Per il secondo osservatore quindi i due eventi, "luce che raggiunge la testa" e "luce che raggiunge la coda", non sono simultanei. Un segnale luminoso colpisce con un certo anticipo il dispositivo che si avvicina verso la luce. L'osservatore di terrà dirà che i due orologi non sono sincronizzati: segnano la stessa ora per eventi che non accadono esattamente nello stesso istante. In conclusione possiamo dire che la simultaneità è un concetto relativo. Contrariamente a quanto l'esperienza quotidiana suggerisce, a velocità confrontabili con quella della luce il tempo diviene quindi relativo al sistema di riferimento.
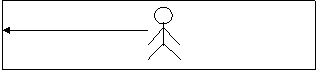

![]()
![]()
![]()
![]()
![]()
La dilatazione dei tempi
Ciò presuppone però una dilatazione del tempo. Immaginiamo nello stesso treno un segnale luminoso che venga inviato perpendicolarmente dal pavimento al soffitto. Per noi osservatori esterni, durante il tragitto del raggio luminoso il treno si andrà progressivamente spostando, quindi il raggio percorrerò una traiettoria obliqua, più lunga della perpendicolare percepita dai passeggeri nel treno. Notiamo, nel treno in movimento che l'osservatore passeggero del treno osserva il raggio muoversi di moto rettilineo uniforme. L'osservatore esterno, che vede il treno muoversi, osserva che il raggio luminoso non si muove su una linea retta ma attraversa delle lunghezze oblique.
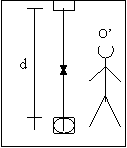
Dal punto di vista del passeggero del treno O', il percorso del lampo
di luce è due volte la distanza fra il punto di emissione e lo specchio. Detto ![]() il tempo che passa prima che il
lampo, propagandosi a velocità c, venga assorbito, si ha:
il tempo che passa prima che il
lampo, propagandosi a velocità c, venga assorbito, si ha:
c ![]() = 2 d
= 2 d
![]()
![]() = 4
= 4 ![]()
![]()
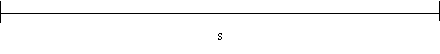

Dal punto di vista
dell'osservatore a terra O, per il quale il treno viaggia con velocità costante
![]() , il percorso della luce è due volte la diagonale di un rettangolo di
altezza d e base s/2, dove s = v
, il percorso della luce è due volte la diagonale di un rettangolo di
altezza d e base s/2, dove s = v ![]() è la distanza percorsa dal treno
nel tempo
è la distanza percorsa dal treno
nel tempo ![]() fra l'emissione e l'assorbimento
del lampo. Poiché anche rispetto all'osservatore di terra la velocità della
luce è c, si ha:
fra l'emissione e l'assorbimento
del lampo. Poiché anche rispetto all'osservatore di terra la velocità della
luce è c, si ha:
![]()
![]()
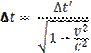
Se
![]() è l'intervallo di tempo fra due
eventi, misurato da un osservatore per il quale essi accadono in uno stesso
punto delle spazio, l'intervallo di tempo
è l'intervallo di tempo fra due
eventi, misurato da un osservatore per il quale essi accadono in uno stesso
punto delle spazio, l'intervallo di tempo ![]() fra gli stessi eventi, misurato da
un secondo osservatore in modo rettilineo uniforme con velocità di modulo v
rispetto al primo è:
fra gli stessi eventi, misurato da
un secondo osservatore in modo rettilineo uniforme con velocità di modulo v
rispetto al primo è:
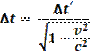
Alla luce di questo esperimento definiamo tempo proprio l'intervallo di tempo misurato dall'osservatore nel proprio sistema di riferimento in cui l'orologio è in quiete. Definiamo invece il tempo non proprio l'intervallo di tempo misurato dall'osservatore rispetto al quale il treno è in moto con velocità v.
La contrazione delle lunghezze
Immaginiamo di osservare un'astronave che
si muove con velocità ![]() dalla Terra in direzione di Plutone.
dalla Terra in direzione di Plutone.
Plutone
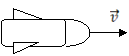

![]()
![]()
![]()
![]() d
d
Per gli osservatori terrestri Terra e Plutone sono separati da una
distanza d e, per percorrerla con velocità costante ![]() , l'astronave impiega un tempo
, l'astronave impiega un tempo ![]() tale che:
tale che:
d = v ![]()
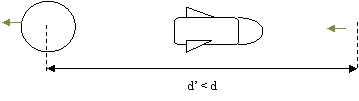
![]()
![]()
Dal punto di vista degli astronauti, i due pianeti transitano con
velocità - ![]() , a un intervallo di tempo
, a un intervallo di tempo ![]() ' l'uno dall'altro, per il luogo in cui è ferma l'astronave. Per la
legge della dilatazione dei tempi, essendo
' l'uno dall'altro, per il luogo in cui è ferma l'astronave. Per la
legge della dilatazione dei tempi, essendo ![]() un tempo proprio, si ha:
un tempo proprio, si ha:
![]()
![]()
Quindi, la distanza Terra- Plutone è:
d'= v ![]()
![]() v
v ![]() =
= ![]() d
d
Se d è la distanza fra due punti misurata
da un osservatore che li vede fermi, la distanza d' fra gli stessi punti,
per un secondo osservatore in moto rispetto al primo con velocità costante d' =
![]() parallela alla retta che congiunge i due punti, è:
parallela alla retta che congiunge i due punti, è:
![]() d
d
Legge della contrazione delle lunghezze
Definiamo quindi lunghezza propria la lunghezza di un segmento misurata rispetto al sistema di riferimento inerziale in cui questi è fermo.
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Chimica |  |
| Lezioni Biologia |  |