 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2307 | Gradito: |
Leggi anche appunti:Tesina sulla relativitàTesina sulla relatività Introduzione. Il XX secolo è stato teatro di La deflessione dei raggi luminosiLa deflessione dei raggi luminosi La prima verifica sperimentale della deflessione L'oscillatore armonicoL'OSCILLATORE ARMONICO Il moto armonico si può sempre descrivere come proiezione |
 |
 |
IL LAVORO MECCANICO
Introduciamo ora un concetto - quello di lavoro meccanico - che può risultare in alcuni casi in contrasto con l'idea di lavoro presente nel linguaggio comune. Spesso si pensa al lavoro in termini di fatica, per cui si è portati a pensare che per tener ferma e sollevata da terra una valigia si debba compiere un qualche lavoro. In Fisica non è così: si parla di lavoro solo quando le forze applicate sugli oggetti sono associate al movimento degli oggetti stessi: nel caso della valigia dunque per la fisica non si compie lavoro per il semplice fatto che, pur applicando una forza, la si tiene ferma. Anticipiamo qui che c'è un altro caso notevole ove il concetto di lavoro meccanico cozza contro il senso comune: per la fisica non si ha lavoro meccanico ogni volta che, pur avendo forza e spostamento, la forza si manifesta ortogonalmente (a 90°) allo spostamento.
Gli ingredienti del lavoro meccanico sono dunque:
LE FORZE F
GLI SPOSTAMENTI S
e possiamo in prima istanza calcolare il lavoro tramite il prodotto forza per spostamento:
W = F S (5.0.1)
La lettera W associata al lavoro serve a ricordare l'inglese work. Dalla (5.0.1) si deduce che l'unità di misura del lavoro è il "Newton per metro", cui si da il nome di Joule (J). Il Joule è anche l'unità di misura (nel Sistema Internazionale) dell'energia; per lavoro ed energia sono anche usate le unità piccola caloria (cal) e grande caloria (Cal), detta anche chilocaloria (Kcal):
1 cal = 4,19 J (5.0.2)
1 Kcal = 4190 J (5.0.3)
Possiamo dire che un Joule è il lavoro compiuto da una forza di un Newton quando il suo punto di applicazione di sposta di un metro in direzione della forza stessa.
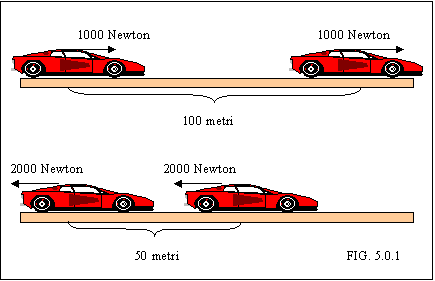 PROBLEMA 1:calcolare il lavoro compiuto dal motore che fa accelerare
per 100 metri la Ferrari di Fig. 5.0.1.
PROBLEMA 1:calcolare il lavoro compiuto dal motore che fa accelerare
per 100 metri la Ferrari di Fig. 5.0.1.
SVOLGIMENTO: dalla formula (5.0.1) segue che
W = 1000N 100m = 100000J.
PROBLEMA 2: calcolare il lavoro compiuto dai freni della Ferrari di fig. 5.0.1.
SVOLGIMENTO: prendendo come positivo il verso da sinistra a destra, notiamo come lo spostamento S valga +50 metri, mentre la forza F valga -2000 Newton; il lavoro vale dunque:
W = -2000N 50m = -100000 J.
I due problemi appena risolti mettono in esistenza che il lavoro è una quantità scalare che può essere positiva o negativa:
quando il lavoro è positivo diciamo che la forza compie lavoro motore, quando è negativo diciamo che compie lavoro resistente. Notiamo come le forze di attrito, essendo sempre opposte alle velocità e dunque agli spostamenti, compiono sempre lavoro resistente (negativo) e vengono dunque dette dissipative (anticipiamo che un lavoro negativo implica una perdita di energia).
LAVORO COMPIUTO DA UNA FORZA NON PARALLELA ALLO SPOSTAMENTO
 Nel paragrafo
precedente ci siamo occupati del lavoro meccanico compiuto da forze costanti
aventi la stessa direzione dello spostamento (al massimo aventi verso opposto,
come nel caso del lavoro resistente). Poiché forze e spostamenti sono vettori,
questi possono avere in generale direzioni diverse. Nella figura 5.1.1, per
esempio, un uomo viene tirato per un tratto S verso destra da una tartaruga mediante una forza F esercitata in direzione basso-destra.
Nel paragrafo
precedente ci siamo occupati del lavoro meccanico compiuto da forze costanti
aventi la stessa direzione dello spostamento (al massimo aventi verso opposto,
come nel caso del lavoro resistente). Poiché forze e spostamenti sono vettori,
questi possono avere in generale direzioni diverse. Nella figura 5.1.1, per
esempio, un uomo viene tirato per un tratto S verso destra da una tartaruga mediante una forza F esercitata in direzione basso-destra.
Come calcoliamo il lavoro in questo caso?
Se scomponiamo il vettore F nelle sue componenti Fpar e Fort aventi la direzioni rispettivamente parallela e ortogonale allo spostamento S, ci accorgiamo che solamente Fpar può "contribuire" al lavoro, dato che la persona non fa alcuno spostamento in direzione ortogonale. Possiamo dunque dire che:
W = Fpar S (5.1.1)
Poiché Fpar = F cos(q) (5.1.1) diventa:
W = F S cos(q (5.1.2)
e dunque il lavoro è uguale a forza per spostamento per coseno dell'angolo fra forza e spostamento.
La formula (5.1.2) è veramente generale e contiene come casi particolari quello per cui forza e spostamento hanno la stessa direzione e lo stesso verso (q = 0°, cos(0°) = 1, W = F S 1 = F S), quello ove F ha verso opposto a S (q = 180°, cos(180°) = -1, W = F S -1 = -F S T lavoro resistente).
Particolare attenzione va prestata al caso delle forze ortogonali agli spostamenti:
in questo caso q = 90°, cos(90°) = 0 e
W = F S (5.1.3)
Una forza ortogonale allo spostamento non compie dunque mai lavoro. Esempi di forze di questo tipo sono le forze centripete (dirette verso il centro della circonferenza e dunque sempre ortogonali agli spostamenti che avvengono sulla circonferenza), le forze magnetiche sulle cariche in moto, le forze di reazione vincolare per i corpi che si muovono su piani.
L'operazione fatta in (5.1.2) che, partendo dai vettori F ed S, fornisce lo scalare "lavoro" moltiplicando i moduli dei due vettori per il coseno dell'angolo compreso viene detta prodotto scalare di due vettori ed indicata in questo modo:
W = F S (5.1.4).
ESEMPIO: il vettore a ha modulo 10, il vettore b ha modulo 5. L'angolo tra i due vettori è di 120°. Calcolare il prodotto scalare tra i due vettori.
a b = a b cos(120°) = 10
IL LAVORO COMPIUTO DA UNA FORZA NON COSTANTE
Prima di occuparci effettivamente del lavoro delle forze non costanti, vediamo l'importantissima traduzione "grafica" del concetto di lavoro nel caso delle forze costanti.
Riferiamoci alla Ferrari che accelera per 100 metri sottoposta alla forza di 1000N di figura 5.0.1 e descriviamo la situazione mediante un grafico che abbia sull'asse x lo spostamento e sull'asse y la forza:
Fig. 5.0.2![]()

il movimento della Ferrari nei primi cento metri
è descritto dal primo dei tre rettangoli disegnati. Calcoliamone l'area:
A = 100
L'area del rettangolo, essendo la base coincidente allo spostamento e l'altezza alla forza, coincide proprio con il lavoro come calcolato nel Problema1 del paragrafo 5.0.
È chiaro da questo esempio come il significato "grafico" di lavoro sia quello di area tra grafico e asse delle ascisse quando si riportino gli spostamenti in ascissa e le forze in ordinata.
Il grafico di figura 5.2.1 suppone che la Ferrari in questione, dopo i primi cento metri nei quali la forza era costante a 1000N, si sia spostata con la seguente modalità: nei successivi 100 metri la forza è scesa a 500N, per altri 100 metri è salita a 2000N, mentre negli ultimi 100 metri l'auto ha frenato con una forza (negativa) di 300N. Quale sarà il lavoro totale compiuto nei 400 metri dalla forza non costante?
Forti del significato grafico del concetto di lavoro appena delineato siamo in grado di trovarlo facilmente:
W = 1000 100 = 320.000 J (5.2.1)
Notiamo come l'area dell'ultimo rettangolo vada presa "negativa" essendo il rettangolo "sotto" l'asse delle x.
Notiamo pure come il calcolo del lavoro rappresenti in certo qual modo il "riassunto" del comportamento di un corpo: in questo senso il lavoro è una grandezza integrale.
IL LAVORO COMPIUTO DALLA FORZA PESO
Supponiamo che un oggetto di massa m cada per un tratto h sottoposto alla forza peso F = m g. Quanto vale il lavoro compiuto dalla forza peso?
Notiamo intanto che siamo nel caso di forza costante, poiché la forza peso in prossimità della terra vale sempre F = m g, e che la forza ha la stessa direzione e verso dello spostamento.
Il lavoro vale dunque:
W = m g h (5.2.1.1)
ESEMPIO1: trova il lavoro compiuto dalla forza peso che fa cadere un peso di 50 Kg per un tratto di 1 Km.
W = 50Kg 9.8m/s2 1000 m = 490000 J
Supponiamo ora di sollevare a velocità costante una massa m per un tratto h. Quanto lavoro compiamo noi? E quanto ne compie la forza di gravità?
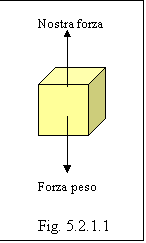 L'oggetto è sotto posto a due forze: la forza di gravità pari a m g e la nostra forza, che in prima istanza può sembrare sconosciuta. Noi
abbiamo detto però che solleviamo l'oggetto a
velocità costante, ovvero con accelerazione nulla; se l'accelerazione è
zero allora anche la forza totale agente sul sistema deve essere zero(ricordate
la seconda legge di Newton?) e dunque la nostra forza deve essere uguale e contraria alla forza di gravità
e valere dunque in modulo m g.
L'oggetto è sotto posto a due forze: la forza di gravità pari a m g e la nostra forza, che in prima istanza può sembrare sconosciuta. Noi
abbiamo detto però che solleviamo l'oggetto a
velocità costante, ovvero con accelerazione nulla; se l'accelerazione è
zero allora anche la forza totale agente sul sistema deve essere zero(ricordate
la seconda legge di Newton?) e dunque la nostra forza deve essere uguale e contraria alla forza di gravità
e valere dunque in modulo m g.
Calcoliamo dunque il lavoro della nostra forza; notiamo come la nostra forza abbia la stessa direzione dello spostamento (entrambe sono verso l'alto) dando luogo così ad un lavoro motore:
Wnostro = m g h
Poiché la forza di gravità e lo spostamento hanno direzioni opposte, il lavoro della forza peso sarà negativo (lavoro resistente):
Wgravità = -m g h.
Se ora calcoliamo il lavoro totale, ovvero il lavoro compiuto da tutte le forze agenti sul sistema, otteniamo:
Wtotale = Wnostro + Wgravità = 0 (5.2.1.2)
Il lavoro totale potrebbe essere anche ottenuto moltiplicando la forza totale per lo spostamento ottenendo la stesso risultato della somma dei lavori parziali rappresentata da (5.2.1.2):
Wtotale = Ftotale S = (m g - m g) h = 0 (5.2.1.3)
IL LAVORO COMPIUTO DALLE MOLLE
Mentre la forza peso su un corpo di massa m è costante e vale m g, la forza esercitata da una molla dipende da quanto la molla viene compressa o tirata. La legge di Hooke, che descrive il comportamento delle molle, dice infatti che:
F = -k x (5.2.2.1)
ove k è una costante caratteristica della molla in esame (costante elastica) e x lo spostamento dalla posizione in cui la molla è "a riposo".
![]()
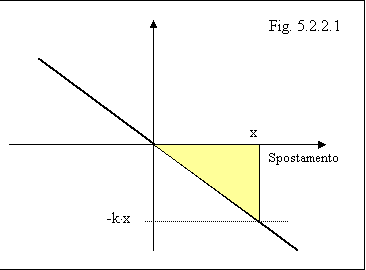 Sappiamo che una legge del tipo y = -a x + b è rappresentata nel piano cartesiano da una retta di coefficiente
angolare a e intercetta b; se rappresentiamo la (5.2.2.1) nel piano cartesiano,
mettendo al posto dell'asse y la forza F, avremo allora una retta di
coefficiente angolare -k e intercetta nulla (passante per l'origine e per il II
e IV quadrante).
Sappiamo che una legge del tipo y = -a x + b è rappresentata nel piano cartesiano da una retta di coefficiente
angolare a e intercetta b; se rappresentiamo la (5.2.2.1) nel piano cartesiano,
mettendo al posto dell'asse y la forza F, avremo allora una retta di
coefficiente angolare -k e intercetta nulla (passante per l'origine e per il II
e IV quadrante).
Supponiamo di spostare di un tratto x verso destra la molla (a velocità costante): per far questo dovremo esercitare una forza che è sempre uguale e contraria a quella della molla (vedi paragrafo precedente). Quanto vale il lavoro compiuto dalla molla?
Grazie alla figura 5.2.2.1 possiamo subito notare come questo lavoro sarà negativo (grafico "sotto" l'asse degli spostamenti), e ciò traduce il fatto che mentre tiriamo la molla a destra questa tende ad opporsi allo spostamento con una forza verso sinistra (lavoro resistente).
Per il calcolo effettivo del lavoro basta calcolare l'area del triangolo in colore:
Wmolla = -(x k x)/2 = -1/2 (k x2) (5.2.2.2)
Quanto vale il lavoro compiuto dalla nostra forza? Poiché la nostra forza è sempre uguale e contraria a quella della molla il nostro lavoro sarà semplicemente uguale al lavoro della molla ma cambiato di segno:
Wnostro = 1/2 (k x2) (5.2.2.3)
LA POTENZA
Supponiamo di dover portare il nostro peso (50 Kg) dal pian terreno sino al 10° piano (30 metri sopra il piano terra): possiamo usare l'ascensore (impiegando 60 secondi) o fare le scale (impiegando 5 minuti = 300 secondi). Se ci premuriamo di salire (a piedi o con l'ascensore) a velocità costante, sappiamo dal 5.2.1 che il lavoro fatto dal motore dell'ascensore o dalle nostre gambe è lo stesso e vale:
W = m g h = 50Kg 9.8m/s2 30m = 14700 J (5.3.1)
Dal 5.2.1 sappiamo anche che questo lavoro è uguale e contrario a quello fatto dalla forza di gravità.
Il fatto che l'ascensore sia più potente delle nostre gambe non è dunque legato alla quantità di lavoro svolto in un certo percorso. Possiamo comunque notare come l'ascensore, per fare i suoi 14700 J, impiega solo 60 secondi, contro i 300 secondi necessari alle nostre gambe.
Se definiamo potenza esercitata da una forza il rapporto tra lavoro compiuto e tempo impiegato, otteniamo una grandezza che rende bene conto della maggiore potenza dell'ascensore rispetto alle nostre gambe:
P = W/Dt (5.3.2)
L'unità di misura della potenza nel Sistema Internazionale è il Joule/secondo detto anche Watt (W).
Diciamo che una forza dà una potenza di 1 W quando fornisce un lavoro di un Joule in un secondo e che la potenza corrisponde al lavoro fatto da una forza nell'unità di tempo.
Calcoliamo dunque le potenze dell'ascensore e delle nostre gambe:
Pascensore = 14700/60 = 245W
Pgambe = 14700/300 = 49W
Ricordando che il lavoro W è uguale a F DS possiamo scrivere:
P = W/Dt = F DS/Dt = F v (5.3.3)
Si può ottenere dunque la potenza anche moltiplicando la forza per la velocità.
Una unità di misura ancora abbastanza usata per la potenza è il cavallo vapore, indicato con CV o HP (Horse Power); la relazione con il Watt è la seguente:
1 CV = 735W = 0.735W (5.3.4)
ESERCIZIO: una Fiat Uno, procedendo alla velocità costante di 140 Km/h, è sottoposta ad una forza d'attrito dovuta all'aria di 850 N. Calcola la potenza erogata dal motore in KW e in CV.
SVOLGIMENTO: per calcolare la potenza erogata dal motore tramite la (5.3.3) ci serve la forza fornita dal motore. Poiché l'auto, pur sotto la spinta del motore, si muove a velocità costante, vuol dire che la forza fornita dal motore è uguale e contraria a quella d'attrito: quindi anche la forza del motore è di 850N. La velocità in m/s vale 140/3,6 39. Da (5.3.4) segue dunque:
Potenza motore = 850N 39 m/s = 33150W = 33.15 KW = 45.1 CV (mai sentito parlare di Uno 45?)
Nelle nostre case la potenza elettrica installata è di circa 3 KW. Cosa vuol dire?
Facciamo l'esempio con un solo KW. Vuol dire che tutti gli elettrodomestici, funzionando insieme, possono fornire un lavoro di 1000 J per ogni secondo del loro funzionamento (ricordate che la potenza ha il significato di lavoro fatto nell'unità di tempo?). Quanto lavoro può fornire in un'ora il KW installato?
Se il lavoro è di 1000J per ogni secondo, in un'ora il lavoro sarà di:
1000J/s 3600s = 3600000 J
A tale lavoro si associa il nome di chilowattora (KWh): questo è infatti il lavoro prodotto in un'ora da una forza che abbia la potenza di un chilowatt.
Il chilowattora è dunque una unità di misura per il lavoro alternativo al Joule e alla caloria.
 |
| Appunti su: |
|
| Appunti Biologia |  |
| Tesine Geografia |  |
| Lezioni Chimica |  |