 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3805 | Gradito: |
Leggi anche appunti:Controlli non distruttiviControlli non distruttivi I Controlli Non Distruttivi (CND) sono il complesso La Controversia - Galvani -VoltaLa Controversia Galvani -Volta A cura di Riccardo Rosa Alessandro Volta Le forze di reazione vincolareLE FORZE DI REAZIONE VINCOLARE Le tre figure a lato rappresentano |
 |
 |
Cenni sull'ellissoide
Finora abbiamo considerato la Terra come un corpo perfettamente sferico, e questa approssimazione era più che sufficiente per spiegare i fenomeni che riguardano la navigazione. In realtà il nostro pianeta è schiacciato ai poli perciò è più assimilabile ad un solido detto ellissoide di rotazione studiato approfonditamente in geodesia[1]. Questo solido è generato dalla rotazione, di 180°, di un'ellisse intorno alla retta su cui giace il suo semiasse minore. Diamo di seguito i valori degli elementi caratteristici dell'ellissoide terrestre, stabiliti dal Sistema Convenzionale Terrestre (World Geodetic System), denominato con la sigla WGS '84 , dall'anno degli ultimi rilievi ufficiali:
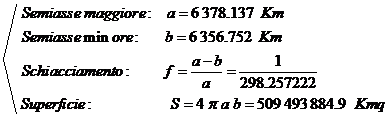
Anche sull'ellissoide terrestre è possibile
stabilire un sistema di coordinate ![]() e
e ![]() , in
analogia a quanto avviene sulla sfera. Tuttavia nel far ciò si commette un
errore, in latitudine. Infatti mentre sulla sfera la verticale in qualsiasi
punto P della superficie coincide con la congiungente di P col centro, ciò non
avviene sulla superficie ellissoidea.
, in
analogia a quanto avviene sulla sfera. Tuttavia nel far ciò si commette un
errore, in latitudine. Infatti mentre sulla sfera la verticale in qualsiasi
punto P della superficie coincide con la congiungente di P col centro, ciò non
avviene sulla superficie ellissoidea.
Osservando la figura, possiamo notare che tra
la normale n in P (verticale) e la retta OP si forma un angolo ![]() ,
denominato angolo alla verticale.
,
denominato angolo alla verticale.
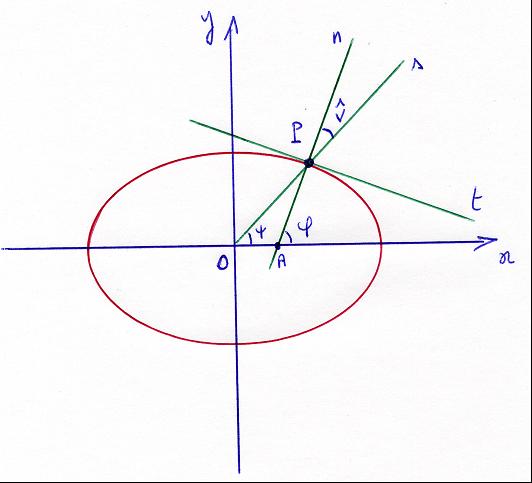

Detti ψ l'angolo che la semiretta OP
forma con l'asse delle ascisse e φ l'angolo che la verticale in P forma
con lo stesso asse di riferimento, possiamo osservare che per noti teoremi di
geometria elementare è: ![]() , onde:
, onde:
![]() ( 1 )
( 1 )
Applicando le formule di addizione e sottrazione, abbiamo:
![]() ( 2 )
( 2 )
Poiché P appartiene all'ellisse di equazione ![]() , allora:
, allora:
![]() ( 3 )
( 3 )
Derivando implicitamente la ![]() abbiamo:
abbiamo:
![]()
![]()
perciò il coefficiente angolare della retta tangente l'ellisse in P è:
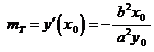
Per la condizione di ortogonalità tra due rette è:
![]()
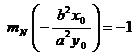
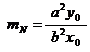
Poiché ![]() è il coefficiente angolare della normale in P
allora esso è uguale alla tangente dell'angolo che la normale forma con l'asse
delle ascisse, perciò:
è il coefficiente angolare della normale in P
allora esso è uguale alla tangente dell'angolo che la normale forma con l'asse
delle ascisse, perciò:
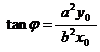 ( 4 )
( 4 )
Sostituendo le ( 3 ) e ( 4 ) nella ( 2 ) abbiamo:
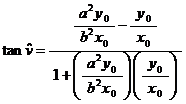
A passaggi effettuati, avendo tenuto conto del
fatto che ![]() e che
e che ![]() , e
generalizzando le coordinate in quanto P può essere un qualsiasi punto della
curva, si ha:
, e
generalizzando le coordinate in quanto P può essere un qualsiasi punto della
curva, si ha:
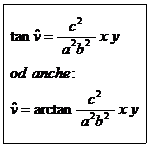 ( 5 )
( 5 )
Le ( 5 ) esprimono l'angolo alla verticale in un qualsiasi punto dell'ellissoide.
Osserviamo subito che:
a) l'angolo alla verticale varia al variare di P lungo l'ellisse
b)
![]() quando è
quando è ![]() oppure quando è
oppure quando è ![]() ; pertanto
possiamo dire che l'angolo alla verticale è nullo nei vertici dell'ellisse.
; pertanto
possiamo dire che l'angolo alla verticale è nullo nei vertici dell'ellisse.
Studiamo la funzione ![]() , di cui
alla seconda delle ( 5 ), in modo da trovare i punti ( se esistono) nei quali
l'angolo alla verticale ha un massimo; limiteremo lo studio al primo quadrante,
potendosi estendere poi i risultati agli altri quadranti tenendo conto delle
simmetrie rispetto agli assi. Derivando implicitamente la ( 5 ) abbiamo:
, di cui
alla seconda delle ( 5 ), in modo da trovare i punti ( se esistono) nei quali
l'angolo alla verticale ha un massimo; limiteremo lo studio al primo quadrante,
potendosi estendere poi i risultati agli altri quadranti tenendo conto delle
simmetrie rispetto agli assi. Derivando implicitamente la ( 5 ) abbiamo:
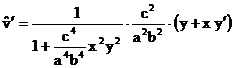
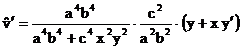
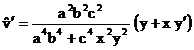
Poiché 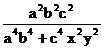 è sempre positivo, è sufficiente studiare la
disequazione:
è sempre positivo, è sufficiente studiare la
disequazione:
![]()
Tenendo conto che ![]() , allora:
, allora:
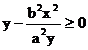
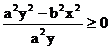
Poiché nel primo quadrante ![]() , è sufficiente studiare la disequazione:
, è sufficiente studiare la disequazione:
![]()
Tenendo conto che è ![]() , abbiamo:
, abbiamo:
![]()
![]()
![]()
![]()
Il segno della derivata prima si ottiene dallo
studio della disequazione: 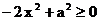 ; risulta
pertanto:
; risulta
pertanto:
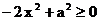 per
per ![]() ; in questo intervallo la funzione
; in questo intervallo la funzione ![]() è crescente;
è crescente;
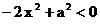 per
per ![]() ; in questo intervallo la funzione
; in questo intervallo la funzione ![]() è decrescente;
è decrescente;
la funzione ![]() ha un massimo relativo in
ha un massimo relativo in ![]() .
.
Concludendo, l'angolo alla verticale è massimo nel punto
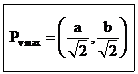 ( 6 )
( 6 )
In questo punto l'angolo alla verticale vale :
![]()
![]()
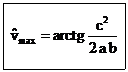 ( 7 )
( 7 )
In corrispondenza del valore massimo dell'angolo alla verticale è facile far vedere che:
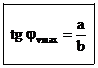 (
8 )
(
8 )
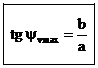 ( 9 )
( 9 )
Per l'ellissoide terrestre, utilizzando i dati del WGS '84, si ha:
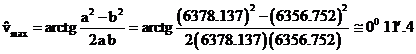
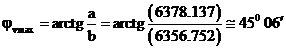
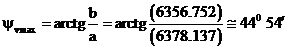
Un altro argomento interessante circa
l'ellissoide di rotazione è quello relativo al calcolo dell'area della sua
superficie. Di norma si esegue con applicazioni del calcolo integrale che,
però, chi scrive non ha ancora studiato. Tuttavia siamo già in grado di
determinare almeno l'area della superficie dell'ellisse che generatrice. Sia ![]() l'area della superficie interna ad un'ellisse.
Essa è data, ricordando che
l'area della superficie interna ad un'ellisse.
Essa è data, ricordando che 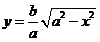 , da:
, da:
![]()
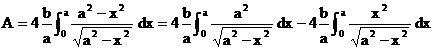
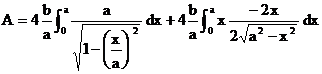
Integrando per sostituzione di variabile il primo integrale e per parti il secondo:
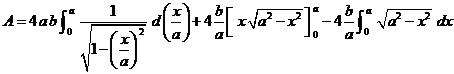
Ma: 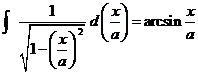 e:
e: ![]() , perciò:
, perciò:
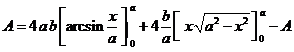
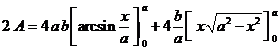
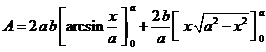
Passando all'integrazione definita:
![]()
![]()
![]()
Ed infine:
![]() ( 10 )
( 10 )
che è l'area dell'ellisse. L'area dell'ellissoide, in analogia con quanto avviene per la sfera, sarà:
![]() ( 11 )
( 11 )
 |
| Appunti su: appuntimania, |
|
| Appunti Biologia |  |
| Tesine Chimica |  |
| Lezioni Geografia |  |