 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 8426 | Gradito: |
Leggi anche appunti:Tipi di bilance presenti nel laboratorioTIPI DI BILANCE PRESENTI NEL LABORATORIO La bilancia è uno strumento di misura La probabilità quantistica ed il microscopio di FeynmanLa probabilità quantistica ed il microscopio di Feynman Al di là della naturale Legge di Hess (1840)Legge di Hess (1840) La somma algebrica dei calori prodotti o assorbiti durante |
 |
 |
Per un generico passaggio di stato o di fase di un sistema costituito da una unica specie chimica, nel quale cioè le due fasi hanno uguale composizione e sono in reciproco equilibrio, vale l'equazione di Clapeyron (ottenuta eguagliando le energie libere di ciascuna fase).
![]()
dove
ΔHPdS = è l'entalpia associata al passaggio di stato A→B
VA = volume occupato dalla fase A
VB = volume occupato dalla fase B
E, tenendo conto che ΔS = ΔH/T, si può anche scrivere
![]()
a) Nel caso dell'equilibrio solido-liquido l'equazione di Clapeyron si scrive
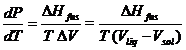
Introducendo per semplicità l'approssimazione che DHfus e DV siano, entro certi limiti, indipendenti dalla temperatura, integrando si ottiene
![]()
Sottraendo membro a membro la relazione per due diverse temperature T1 e T2 si arriva all'equazione approssimata della curva di coesistenza solido-liquido:
![]()
Se invece integriamo la relazione di Clapeyron espressa in funzione della variazione di entropia otteniamo
![]()
Una retta di pendenza DS DV. Poiché sia l'entalpia che l'entropia di fusione sono positive (durante il processo di fusione il sistema assorbe il calore latente (DH>0) e diventa più disordinato(DS>0)), la pendenza della curva solido-liquido dipende dal segno di ΔV.
La maggior parte delle sostanze ha una pendenza positiva della curva di fusione (all'aumentare della pressione la temperatura di fusione aumenta) in quanto la fase liquida presenta un volume maggiore della fase solida (ΔV = Vliquido - Vsolido > 0). L'acqua è una nota eccezione, poiché ΔV < 0 (il ghiaccio è meno denso e quindi più voluminoso dell'acqua liquida)
Esempio
Valutare la variazione di pressione necessaria per abbassare di 1 °C il punto di fusione del ghiaccio, sapendo che la densità dell'acqua è pari a 0.9998 g cm-3 e quella del ghiaccio è pari a 0.917 g cm-3, assumendo che il valore del ΔHfus sia indipendente dalla pressione e sia pari 6.0095 kJ mol-1.
Calcoliamo il volume occupato da una mole di acqua (peso molare = 18,015 g mol-1) liquida e solida ed il relativo ΔV
V (ghiaccio) = ![]() = 19.6456 cm3
mol 19.6456 10-6 m3
mol
= 19.6456 cm3
mol 19.6456 10-6 m3
mol
V(acqua) = ![]() = 18.0186 cm3 mol 18.0186 10-6 m3 mol
= 18.0186 cm3 mol 18.0186 10-6 m3 mol
ΔV = V(acqua) - V(ghiaccio) = -1.627 10-6 m3 mol
Sostituiamo ora i valori nella equazione di Clapeyron e ricordando che 1 atm = 101325 Pa
![]() = 1.36484 107 Pa = 134.7 atm
= 1.36484 107 Pa = 134.7 atm
Il movimento dei ghiacciai contro ostacoli rocciosi è attribuito in parte a questo abbassamento del punto di fusione indotto dalla forte pressione esercitata dalla massa di ghiaccio contro la roccia.
b) Se una delle due fasi è gassosa e quindi nel caso di equilibrio fase condensata-fase gassosa, si possono fare le seguenti approssimazioni:
In base a queste approssimazioni, essendo
![]()
e
![]()
l'equazione di Clapeyron per il passaggio di fase di 1 mole in cui una delle fasi è un gas si presenta nella forma seguente, nota come equazione di Clausius-Clapeyron
![]()
che, integrata, diventa
![]()
e trasformando il logaritmo neperiano in un logaritmo in base 10 (coefficiente di conversione 2,3), l'equazione di Clausius-Clapeyron diventa
![]()
ponendo poi la costante di integrazione pari a k = ln(A), l'equazione di Clausius-Clapeyron può essere scritta nella seguente forma esponenziale
![]()
![]()
con A che dipende dalla natura della specie chimica, in cui si osserva che la tensione di vapore di un liquido cresce esponenzialmente con la temperatura T
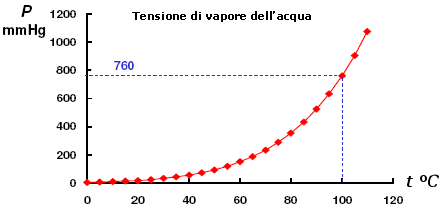
Nei diagrammi di fase le curve della tensione di vapore del liquido e del solido sono calcolabili attraverso l'equazione di Clausius-Clapeyron
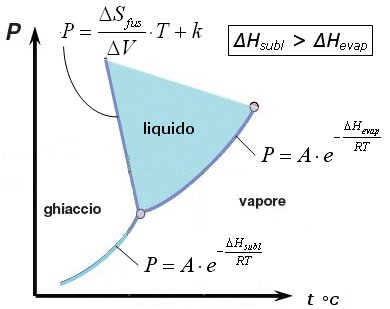
Sottraendo membro a membro l'equazione di Clausius-Clapeyron per due diverse temperature T1 e T2 si ottiene l'equazione di Clausius-Clapeyron in una forma che lega le tensioni di vapor saturo di un liquido o di un solido (sublimazione) a due diverse temperature
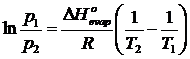
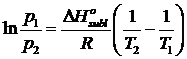
Questa relazione si può usare per prevedere la pressione di vapore ad una data temperatura conoscendo DH ed una pressione di riferimento.
Esempio
Calcolare la pressione di vapore del toluene a 20 C sapendo che la temperatura di ebollizione è 110.6 C e che l'entalpia di evaporazione è 35.2 kJ mol
Alla temperatura di ebollizione di 110.6 + 273.15 = 383.75K la pressione di vapore è per definizione 760 mmHg. Quindi
 = 25 mm Hg
= 25 mm Hg
Inoltre l'equazione di Clausius-Clapeyron può essere utilizzata per ricavare il DH da valori noti di pressione e temperatura.
Esempio
Ricavare l'entalpia di evaporazione del benzene dai dati seguenti:
P (a 70 C) = 547.4 mm Hg; P2 (a 80 C) = 753.6 mm Hg
 = 32.2 kJ mol
= 32.2 kJ mol
Diagrammando i valori del logaritmo naturale della pressione in funzione del reciproco della temperatura si ottengono rette di pendenza DH
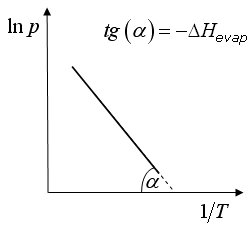
 |
| Appunti su: equazione di clapeyron, clausius clapeyron, equazione di clausius clapeyron, Equazione di Clausius-Clapeyron, equazione clausius clapeyron, |
|
| Appunti Biologia |  |
| Tesine Ingegneria tecnico |  |
| Lezioni Geografia |  |