 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 5127 | Gradito: |
Leggi anche appunti:Limiti di applicabilità della relazione di Henderson-HasselbachLimiti di applicabilità della relazione di Henderson-Hasselbach Nell'equazione Metodo dei tempi di dimezzamentoMetodo dei tempi di dimezzamento Necessita della conoscenza di due valori Legge di GrahamLegge di Graham La velocità con cui un gas fuoriesce da un foro di piccole |
 |
 |
La Teoria degli urti (o Teoria delle collisioni) è un approccio teorico che si fonda sulla teoria cinetica dei gas (meccanica statistica) e dunque fornisce risultati accettabili soprattutto per reazioni in fase gassosa.
Secondo tale modello, affinché le molecole dei reagenti possano produrre una reazione chimica, esse devono urtarsi. In generale dunque la velocità di una reazione deve essere proporzionale alla frequenza degli urti. Tuttavia non tutti gli urti saranno in grado di trasformare i reagenti nei prodotti, ma solo quelli che avverranno con una corretta orientazione e con un'energia cinetica sufficientemente elevata, superiore ad un valore critico, detto energia di attivazione, tale da rompere i vecchi legami e da formare i nuovi.
In altre parole solo una piccola frazione degli urti tra le molecole dei reagenti risulterà possedere le caratteristiche necessarie a produrre la reazione. Gli urti in grado di trasformare i reagenti in prodotti sono definiti urti efficaci.
Urti efficaci = urti totali x frazione urti correttamente orientati x frazione urti sufficientemente energetici
La velocità della reazione dipende quindi dalla frequenza degli urti efficaci (sufficientemente energetici e correttamente orientati). In tal modo possiamo anche spiegarci il motivo per cui la velocità della reazione aumenti in genere all'aumentare della concentrazione dei reagenti. Infatti una maggior concentrazione accresce la probabilità che le particelle si urtino e aumenta quindi anche la frequenza degli urti tra particelle sufficientemente energetiche e correttamente orientate.
Nella teoria degli urti le molecole che partecipano alla reazione sono viste come sfere rigide (hard spheres) le cui dimensioni (diametro d di sfera rigida) e massa influenzano la frequenza degli urti. Vi sono diverse modalità per stimare le dimensioni di sfera rigida di una molecola, tuttavia il modo più semplice è calcolarne il raggio di van der Waals a partire dal valore tabulato della costante b (covolume) di van der Waals, che compare nell'equazione di stato dei gas reali (equazione di van der Waals). La relazione tra covolume b e dimensione di sfera rigida d delle molecole di un gas è, come abbiamo già visto, la seguente
![]()
con N numero di Avogadro
Una buona stima del covolume si può ottenere conoscendo la densità dell'aeriforme liquefatto
Esempio
Stimiamo le dimensioni di sfera rigida della CO2, sapendo che la densità dell'anidride carbonica liquida è 1032 g dm-3
Calcoliamo la concentrazione della CO2 liquefatta (numero di moli per unità di volume), dividendo la densità per la massa molare della CO2.
![]()
calcolando ora il reciproco della concentrazione otteniamo il volume molare del liquido (volume occupato da una mole) che risulta essere una buona stima del covolume b (il covolume tabulato per la CO2 è b = 0,04267 L mol-1)
![]()
Stimiamo ora il diametro di sfera rigida della CO2
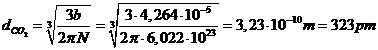
* * * * * *
La teoria degli urti da un significato fisico ai parametri dell'equazione di Arrhenius e dimostra che il fattore esponenziale rappresenta, ad una data temperatura T, la frazione di urti sufficientemente energetici (con energia superiore a Eatt), mentre il fattore pre-esponenziale A viene espresso come prodotto di altri due fattori A = Z∙P, dove:
- Z è il fattore di frequenza correlato alla frequenza totale degli urti. Dipende dalle dimensioni delle particelle (diametro di sfera rigida), dalla loro massa e dalla loro temperatura. Le variazioni di temperatura incidono comunque, come vedremo, in modo trascurabile sulla frequenza degli urti rispetto all'elevata influenza che manifestano sul fattore esponenziale
- P è il fattore sterico (o fattore di probabilità) che dipende essenzialmente dalla geometria delle molecole e misura la probabilità che i reagenti, aventi una certa struttura geometrica, si scontrino con un opportuno orientamento.
L'equazione di Arrhenius può dunque essere riscritta nella forma
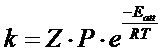
Per ricavare tale relazione procediamo per passi successivi.
Iniziamo ipotizzando che ogni urto tra molecole dei reagenti sia efficace e generi i prodotti di reazione (urto semplice). Questa ipotesi semplificatrice ci permetterà di definire il fattore di frequenza Z.
Fattore di frequenza Z (urto semplice → tutti gli urti sono efficaci→ k = Z)
Per semplicità consideriamo la reazione elementare in fase gassosa
A + B prodotti
L'ipotesi è che la velocità di reazione sia proporzionale alla frequenza degli urti di A con B.
Si consideri allora un contenitore di volume V in cui siano presenti n moli di B. La teoria cinetica dei gas (Meccanica statistica) dimostra che la frequenza ZA degli urti di una molecola A con le nN molecole B (N = numero di Avogadro) è
![]()
dove
![]() è la densità
particellare di B (numero di particelle per unità di volume)
è la densità
particellare di B (numero di particelle per unità di volume)
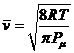 è la velocità
relativa media delle molecole A e B. Pm è
la massa molare ridotta delle molecole A e B, definita come
è la velocità
relativa media delle molecole A e B. Pm è
la massa molare ridotta delle molecole A e B, definita come ![]() . La teoria cinetica dimostra infatti che, alla
medesima temperatura T, molecole di
massa diversa presentano diversa velocità media. Tuttavia si dimostra anche che
il comportamento dinamico del sistema è equivalente se assumiamo che tutte le molecole si muovano con la
velocità media di una particella di massa pari alla loro massa ridotta.
. La teoria cinetica dimostra infatti che, alla
medesima temperatura T, molecole di
massa diversa presentano diversa velocità media. Tuttavia si dimostra anche che
il comportamento dinamico del sistema è equivalente se assumiamo che tutte le molecole si muovano con la
velocità media di una particella di massa pari alla loro massa ridotta.
s è la sezione d'urto. La sezione d'urto relativa a due molecole A e B è l'area attorno alla molecola A in cui deve trovarsi il centro di una molecola B perché avvenga una collisione. Se i diametri delle due molecole sono dA e dB il raggio della sezione d'urto è d dA dB) = (rA + rB) e la sua area è s pd
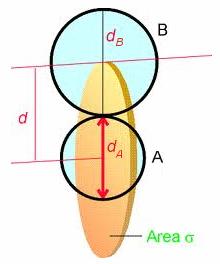
In un secondo la particella A percorrerà uno spazio ![]() ed urterà tutte le particelle il cui centro si
trova all'interno del cilindro disegnato dalla sua sezione d'urto (cilindro d'urto), avente base σ = pd e altezza h =
ed urterà tutte le particelle il cui centro si
trova all'interno del cilindro disegnato dalla sua sezione d'urto (cilindro d'urto), avente base σ = pd e altezza h =![]() .
.
Il cilindro d'urto è il volume spazzato dalla sezione d'urto nell'unità di tempo.
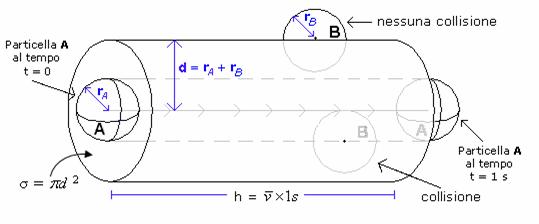
Per calcolare il numero di particelle che si trovano all'interno del
cilindro, e dunque il numero di particelle B che la particella A urta
nell'unità di tempo (ZA), è sufficiente moltiplicare il volume del
cilindro spazzato dalla sezione d'urto (![]() ) per il numero di molecole di B che si trovano
nell'unità di volume (densità particellare di B = ρB).
) per il numero di molecole di B che si trovano
nell'unità di volume (densità particellare di B = ρB).
![]()
Per calcolare il numero di urti ZAB che subiscono tutte
le molecole di A con tutte le molecole di B, nell'unità di tempo e nell'unità
di volume è necessario moltiplicare ZA (urti per particella per
secondo) per la densità particellare di A, pari a ![]() .
.
![]() (s-1 m-3)
(s-1 m-3)
Poiché abbiamo ipotizzato che tutti gli urti siano reattivi, ZAB rappresenta il numero di molecole che reagiscono al secondo per unità di volume e dunque rappresenta la velocità v della reazione.
Per trasformare il numero di molecole che reagiscono nel corrispondente numero di moli è sufficiente dividere la densità degli urti ZAB per il numero di Avogadro
v ![]()
Confrontando la relazione precedente con la legge cinetica
![]()
si ottiene
![]()
La
quantità ![]() è definita fattore di frequenza Z.
è definita fattore di frequenza Z.
In definitiva, se ipotizziamo che tutti gli urti siano efficaci, la costante cinetica k risulta essere uguale al fattore di frequenza Z, il quale può essere calcolato usando la seguente espressione
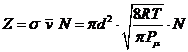
Esempio.
Calcoliamo la costante di velocità per la reazione elementare
H2 + I2 = 2HI
alla temperatura di 300 C, sapendo che i diametri di sfera rigida d(H2) = 272 pm e d(I2) = 635 pm e nella ipotesi che ogni urto dia luogo ad un atto reattivo (k = Z)
La massa molare ridotta per il sistema idrogeno-iodio è data da
![]()
Il diametro medio è
d = ½ (272 + 635) m = 453.5 m
e dunque la sezione d'urto è
s pd2 = 3.14 ) 2 m2 = 6.461 m2
La velocità media relativa si ottiene dall'espressione
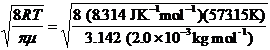 = 2463 m s
= 2463 m s
Infine la costante di velocità è il prodotto
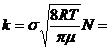 (6.461 m2 ) ( 2463 m s ) ( 6.02 1023 mol
(6.461 m2 ) ( 2463 m s ) ( 6.02 1023 mol
108 m3 mol s 1011 L mol s
Questo numero è enormemente superiore al valore sperimentale di k = 1.15 L mol s
* * * * * * *
Fattore esponenziale
(urto attivato → solo gli urti
attivati sono efficaci → ![]() )
)
I valori teorici di k che si ottengono nell'ipotesi che ogni urto sia efficace (reattivo) sono enormemente più elevati (come abbiamo visto dall'esempio precedente) dei valori sperimentali della costante cinetica. Si ipotizza pertanto che un urto sia efficace a patto che sia attivato, cioè tale che la somma delle energie cinetiche di A e B non sia inferiore ad una soglia detta energia di attivazione:
EA + EB Eatt
La frazione di urti che soddisfano tale condizione si calcola
(Boltzmann) come ![]()
Quindi la costante di velocità diventa
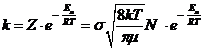
Esempio
Calcoliamo la costante di velocità dell'esempio precedente nell'ipotesi che l'energia di attivazione sia di 170 kJ mol
Il fattore esponenziale si calcola come
![]() = 3.21
= 3.21
Quindi la costante di velocità è data dal prodotto
k = (9.58 1011 L mol s ) ( 3.21 L mol s
Questo numero approssima abbastanza il valore sperimentale di k = 1.15 L mol s , ma tuttavia risulta ancora maggiore.
Esempio
Calcoliamo la fazione di urti sufficientemente energetici a 30°C in una reazione avente Eatt = 15 kJ/mol
![]()
26 urti su 10.000 risultano sufficientemente energetici
* * * * * * *
Il significato fisico attribuito dalla teoria degli urti al fattore esponenziale si colloca all'interno della meccanica statistica. Come abbiamo già visto, la meccanica statistica dimostra che, ad una data temperatura, non tutte le particelle possiedono la stessa energia cinetica, ma le energie cinetiche si distribuiscono in modo caratteristico secondo una curva di frequenza detta maxwelliana.
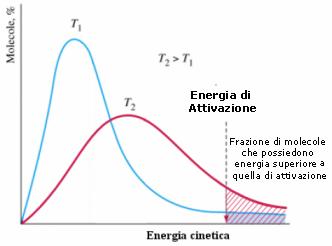
Dall'osservazione del grafico si può facilmente comprendere come, all'aumentare della temperatura, aumenti anche la frazione di molecole che possiede energia superiore all'energia di attivazione.
Si noti infine come una variazione di Temperatura modifichi la velocità di una reazione agendo in modo duplice, producendo effetti sia sul fattore esponenziale che sul fattore di frequenza Z. È tuttavia facile verificare che gli effetti su Z sono trascurabili rispetto agli effetti sul fattore esponenziale.
Esempio
Confrontiamo gli effetti sul fattore esponenziale e sul fattore di frequenza di un aumento di temperatura del 50%, da 303 K a 454,5 K, per una reazione con Eatt = 15 kJ/mol).
Calcoliamo il rapporto dei fattori esponenziali alle due temperature
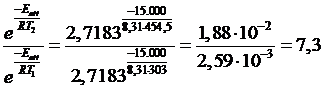
calcoliamo il rapporto dei fattori di frequenza alle due temperature
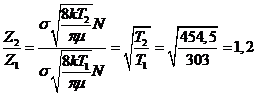
La velocità aumenta di 7,3 volte per il fattore esponenziale e solo del 20% per il fattore di frequenza
* * * * * * *
Fattore sterico P (urto attivato ed orientato → ![]() )
)
I valori teorici delle costanti di velocità, calcolati partendo dall'ipotesi dell'urto attivato, non coincidono in genere (come abbiamo già visto in un esempio precedente) con i valori sperimentali misurati.. Tali differenze sono tanto più vistose quanto più complesse sono le molecole dei reagenti e ciò fa ritenere che le discrepanze con i valori attesi siano da imputare alle diverse geometrie delle molecole che si urtano. Se infatti consideriamo la reale geometria delle molecole, non tutti gli urti avverranno con la corretta orientazione.
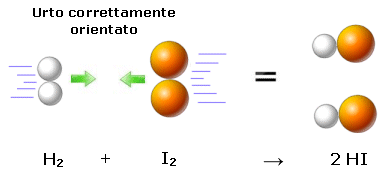
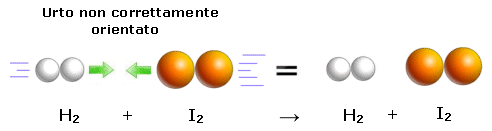
Per risolvere questo problema viene introdotto un fattore correttivo P, noto come fattore sterico (o fattore di probabilità). P rappresenta la probabilità che le molecole dei reagenti coinvolte in un urto siano correttamente orientate e viene definito come il rapporto tra il valore sperimentale misurato e quello teorico calcolato della costante cinetica..
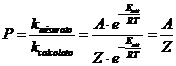
Dalla relazione precedente si osserva come P può essere ottenuto anche come rapporto tra il fattore pre-esponenziale A di Arrhenius ed il fattore di frequenza F definito nella Teoria degli urti.. Si avrà pertanto anche
A = Z∙P
In definitiva, la teoria degli urti esprime il fattore pre-esponenziale di Arrhenius come il prodotto tra il fattore sterico P (che tiene conto della geometria delle molecole) e del fattore di frequenza F (correlato alla frequenza complessiva degli urti tra le molecole)
Esempio
Calcoliamo il fattore sterico P per la reazione di sintesi dell'acido iodidrico dai suoi elementi (H2 + I2 = 2HI) sapendo che il valore sperimentale di k = 1.15 L mol s , mentre il valore calcolato tramite la teoria degli urti (vedi esempi precedenti) è k = 3.07 L mol s
![]()
Ogni 100 urti 37 possiedono la giusta orientazione per essere efficaci.
Esempio
Calcoliamo il fattore sterico P a 2500K per la reazione elementare CO + O2 = CO2 + O sapendo che la costante cinetica a 2500K vale k = 1.22 105 L mol s , mentre a 2800K il suo valore diventa k = 3.66 105 L mol s . Siano inoltre i diametri di sfera rigida d(CO) = 360 pm e d(O2) = 350 pm
stimiamo l'energia di attivazione della reazione
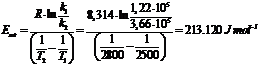
stimiamo il fattore pre-esponenziale A
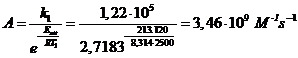
calcoliamo il fattore di frequenza Z
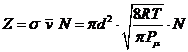
La massa molare ridotta per il sistema CO-O2 è data da
![]()
Il diametro medio è
d = ½ (360 + 350) m = 355 m
e dunque la sezione d'urto è
s pd2 = 3.14 ) 2 m2 = 3.96 m2
La velocità media relativa si ottiene dall'espressione
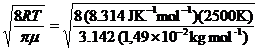 = 1885 m s
= 1885 m s
Infine il fattore di frequenza Z vale
![]() m2 ) ( 1885 m s ) ( 6.022 1023 mol 108 m3 mol s
m2 ) ( 1885 m s ) ( 6.022 1023 mol 108 m3 mol s
1011 L mol s
Calcoliamo infine il fattore di probabilità P
![]()
84 urti correttamente orientati ogni 10.000.
* * * * * * *
Tuttavia, alcune reazioni presentano fattori sterici che assumono valori superiori all'unità. Ciò significa semplicemente che la reazione procede più rapidamente di quanto calcolato in modo teorico attraverso il modello della teoria degli urti. Tipicamente ciò accade per le reazioni in soluzione. Si ricordi infatti che la teoria degli urti è ricavata dalla teoria cinetica dei gas e dunque descrive in modo migliore le reazioni in fase gassosa. Nel caso di reazioni in soluzione, il solvente ha infatti l'effetto di aumentare l'efficacia delle collisioni, producendo valori di P > 1.
Si tenga comunque presente che tutti gli sforzi effettuati per correlare i valori assunti da tale fattore con la struttura o le proprietà molecolari non hanno avuto successo. Sarebbe dunque preferibile limitarsi a considerare il fattore sterico come un generico "fattore di correzione", senza volergli attribuire particolari significati fisici.
 |
| Appunti su: urti totali urti efficaci, teoria degli urti, teoria degli urti limiti, teoria degli urti e fattore sterico, teoria degli urti efficaci, |
|
| Appunti Biologia |  |
| Tesine Geografia |  |
| Lezioni Ingegneria tecnico |  |