 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1829 | Gradito: |
Leggi anche appunti:La termodinamicaLA TERMODINAMICA 2H2O+O2=2H2O Tutti sappiamo che le combustioni sono spontanee, Sali complessiSali complessi Si definiscono complessi quei sali che dissociandosi formano Liquidi e solidiLiquidi e solidi Nella esperienza di Andrews abbiamo visto che i gas possono passare |
 |
 |
Il calcolo del pH di acidi e basi deboli poliprotici, implicando più equilibri di dissociazione, ognuno caratterizzato da una propria costante di equilibrio, risulta essere più complesso. In generale è infatti necessario risolvere sistemi di più equazioni.
Molto spesso accade però che le costanti di dissociazione successive alla prima presentino valori molto minori. In tal caso è possibile dimostrare che la concentrazione di equilibrio degli ioni H+ dipende in pratica solo dal primo equilibrio. Inoltre i calcoli per la determinazione di tutte le concentrazioni di equilibrio possono venire notevolmente semplificati considerando ciascun equilibrio di dissociazione separatamente ed in modo indipendente dagli altri.
Per esemplificare quanto affermato calcoliamo il pH di una soluzione
0,5 M di acido solforoso, sapendo che la costante di prima dissociazione è ![]() , mentre la costante di seconda dissociazione vale
, mentre la costante di seconda dissociazione vale ![]() .
.
I due equilibri di dissociazione sono
H2SO3 ![]() H+ + HSO3-
H+ + HSO3-
HSO3- ![]() H+ + SO32-
H+ + SO32-
Per risolvere correttamente il problema è necessario considerare contemporaneamente i due equilibri in quanto gli ioni H+ prodotti dalla prima dissociazione tendono a spostare verso sinistra il secondo equilibrio e viceversa.
Chiamando x il numero di mol/L di acido solforoso che si dissociano nel primo equilibrio e y il numero di mol/L di HSO3- che si dissociano nel secondo equilibrio, avremo
per il primo equilibrio
|
Specie |
Concentrazioni iniziali |
Concentrazioni all'equilibrio |
|
H2SO3 |
|
0,5 - x |
|
H+ |
|
x + y |
|
HSO3- |
|
x - y |
Infatti alle x mol/L di ioni H+ prodotti dal primo equilibrio è necessario aggiungere le y mol/L di ioni H+ prodotti dal secondo equilibrio, mentre alle x mol/L di anioni HSO3- prodotti dal primo equilibrio è necessario togliere le y mol/L che si dissociano nel secondo equilibrio.
per il secondo equilibrio
|
Specie |
Concentrazioni iniziali |
Concentrazioni all'equilibrio |
|
HSO3- |
|
x - y |
|
H+ |
|
x + y |
|
SO32- |
|
y |
Sarebbe quindi necessario risolvere il seguente sistema di equazioni, che garantisce che entrambe le condizioni di equilibrio siano contemporaneamente soddisfatte.
![]()
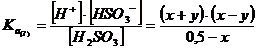

La risoluzione risulta però lunga e laboriosa, generando tra l'altro un'equazione di grado superiore al secondo.
Nel caso si tenga conto anche dell'equilibrio di dissociazione dell'acqua la formula risolutiva esatta è
![]()
con x = [H+]
mentre, se si trascura l'equilibrio di dissociazione dell'acqua, l'equazione si abbassa di un grado e si ha
![]()
In questo caso possiamo comunque risolvere il problema in modo approssimato poiché la costante di seconda dissociazione risulta essere di ben 5 ordini di grandezza inferiore della costante di prima dissociazione e possiamo quindi ragionevolmente ritenere che gli ioni H+ prodotti dal secondo equilibrio siano trascurabili rispetto a quelli prodotti dal primo. E' possibile quindi considerare il primo equilibrio di dissociazione prevalente e procedere alla soluzione separata dei due equilibri.
Prendiamo dunque in considerazione il primo equilibrio come se non fosse presente il secondo
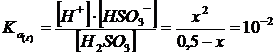
La soluzione dell'equazione di 2° grado ci fornisce il seguente valore
x = [H+]I = [HSO3-] = 6,59.10-2
Dove [H+]I rappresenta la concentrazione di ioni H+ prodotti dalla prima dissociazione.
Utilizziamo ora la concentrazione di HSO3- trovata, come concentrazione iniziale per la seconda dissociazione e teniamo conto in questo caso che gli ioni H+ provenienti dalla prima dissociazione spostano l'equilibrio verso sinistra

Essendo la ka estremamente piccola y avrà un valore che potrà essere tranquillamente trascurato sia nella somma a numeratore che nella differenza a denominatore. Otteniamo in tal modo il seguente risultato
y = [H+]II = [SO32-] = 2,6.10-7
Come si può notare la concentrazione di ioni H+ provenienti dalla seconda dissociazione è talmente bassa che, anche se sommata alla concentrazione degli ioni H+ proveniente dalla prima dissociazione non ne modifica il valore
[H+]tot = [H+]I + [H+] II = x + y = 6,59.10-2 + 2,6.10-7 = 6,59.10-2
Possiamo inoltre verificare che gli ioni H+ provenienti dalla seconda dissociazione sono in concentrazione talmente esigua da giustificare la trattazione separata del primo equilibrio. La loro presenza in soluzione sposta infatti l'equilibrio di prima dissociazione verso sinistra di una quantità assolutamente trascurabile.
In generale è possibile trattare gli equilibri separatamente, senza commettere grossi errori, quando le costanti di dissociazione differiscono di almeno 3 - 4 ordini di grandezza.
Naturalmente quando si considerano separatamente i due equilibri valgono tutte le considerazioni fatte per gli acidi deboli monoprotici.
Sarà dunque necessario scegliere la formula risolutiva semplificata più appropriata in relazione ai valori della concentrazione C e della costante di prima dissociazione acida ka1.
Esempio
Calcoliamo [H+] di una soluzione 10-1 M di acido metasilicico H2SiO3 (ka1 = 2 10-10, ka2 =1 10-12) e di una soluzione 10-5 M del medesimo acido.
Consideriamo solo l'equilibrio di prima dissociazione e verifichiamo le condizioni di applicabilità delle formule semplificate per gli acidi deboli monoprotici.
![]()
![]()
Il pH di una soluzione viene normalmente misurato tramite uno strumento detto piaccametro. Per ottenere una indicazione qualitativa del pH di una soluzione si usano particolari sostanze chimiche dette indicatori.
Un indicatore è generalmente costituito da un acido o da una base debole che assume un colore diverso in relazione al pH della soluzione.
Il valore del pH in corrispondenza del quale un indicatore cambia colore è detto pH di viraggio.
Usando un indicatore unico non è quindi possibile sapere qual è il pH di una soluzione, ma solo se la soluzione presenta un pH superiore o inferiore al pH di viraggio di quell'indicatore.
Per conoscere il valore approssimato del pH di una soluzione è necessario utilizzare una striscia di carta impregnata con più indicatori (indicatore universale), che assume diversi colori a seconda del pH.
Se indichiamo con HIn un generico indicatore costituito da un acido debole, il suo equilibrio di dissociazione sarà
HIn ![]() H+ + In-
H+ + In-
La capacità dell'indicatore di assumere due diversi colori è legata al fatto che la forma indissociata HIn presenta un colore diverso dell'anione In-.
L'equilibrio dell'indicatore si sposta per il principio di Le Chatelier verso destra o verso sinistra, facendo prevalere una delle due forme colorate sull'altra, a seconda che esso si trovi in presenza di una soluzione basica o acida.
Infatti se aumentiamo la [H+] l'equilibrio dell'indicatore tende a spostarsi verso sinistra e prevale HIn, mentre se diminuiamo la [H+] l'equilibrio si sposta verso destra e prevale In-.
Così se l'indicatore viene posto in una soluzione acida, parte degli ioni H+ presenti in soluzione reagiscono con gli ioni In- per ridare la forma indissociata HIn e l'equilibrio dell'indicatore si sposta verso sinistra.
Mentre se l'indicatore viene posto in una soluzione basica, parte degli ioni OH- presenti in soluzione si associano con gli ioni H+ provenienti dalla dissociazione dell'indicatore per formare H2O indissociata (l'equilibrio di dissociazione dell'acqua è infatti molto spostato verso sinistra) . La diminuzione degli ioni H+ costringe l'indicatore a dissociarsi ulteriormente ed il suo equilibrio si sposta verso destra.
Naturalmente il punto di viraggio viene raggiunto quando la concentrazione della specie indissociata HIn eguaglia la concentrazione dell'anione In-.
punto di viraggio [HIn] = [In-]
Il pH di viraggio è facilmente determinabile conoscendo il valore della costante di dissociazione dell'indicatore, infatti

da cui
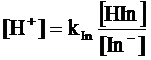
ricordando infine che al punto di viraggio [HIn] = [In-],
allora
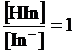
e quindi
![]()
passando infine ai logaritmi, si dimostra che il pH di viraggio è uguale al logaritmo negativo della costante di dissociazione dell'indicatore o pK
![]()
Naturalmente se l'indicatore è una base debole sarà
![]()
e
![]()
In realtà ciascun indicatore vira (cambia colore) in corrispondenza di un intervallo di pH necessario affinché l'occhio possa apprezzare il cambiamento di colore. L'occhio umano riesce infatti ad apprezzare il colore quando le due concentrazioni variano almeno di 10 volte.
Ad esempio per un generico indicatore acido HIn, il colore A predomina quando il rapporto [In-]/[HIn] < 1/10 ed il colore B quando [In-]/[HIn] > 10
L'intervallo di pH di viraggio di un indicatore sarà dunque pari a pkind ± 1. Supponendo ad esempio di impiegare un indicatore acido con ka= 10-5, il viraggio del colore verrà apprezzato quando il pH varia tra 6 e 4 (intervallo di viraggio dell'indicatore). Infatti
quando [HIn] = 10 [In-] si avrà

quando [In-] = 10 [HIn] si avrà
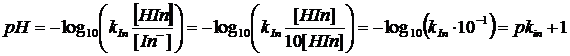
|
Indicatore |
Intervallo di Viraggio (pH) |
Colore |
|
|
Forma acida |
Forma basica |
||
|
Blu timolo |
|
Rosso |
Giallo |
|
|
|
Giallo |
Blu |
|
Blu bromofenolo |
|
Giallo |
Blu |
|
Metilarancio |
|
Rosso |
Giallo-rame |
|
Rosso congo |
|
Blu |
Rosso |
|
Verde di bromocresolo |
|
Giallo |
Blu |
|
Rosso di metile |
|
Rosso |
Giallo |
|
Bromocresolo porpora |
|
Giallo |
Porpora |
|
Blu di bromotimolo |
|
Giallo |
Blu |
|
Rosso fenolo |
|
Giallo-arancio |
Rosso |
|
Cresolo porpora |
|
Giallo |
Rosso-porpora |
|
Fenolftaleina |
|
Incolore |
Rosso |
|
Timoftaleina |
|
Incolore |
Blu |
|
Giallo di alizarina |
|
Incolore |
Violetto |
 |
| Appunti su: appuntimania, |
|
| Appunti Geografia |  |
| Tesine Biologia |  |
| Lezioni Ingegneria tecnico |  |