 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 6085 | Gradito: |
Leggi anche appunti:Il Meccanismo delle Reazioni OrganicheNei casi più semplici, le reazioni possono avvenire in un unico stadio o in due Transizioni di fase: Equazione di Clausius-ClapeyronTransizioni di fase: Equazione di Clausius-Clapeyron Per un generico passaggio BerillioBERILLIO Il berillio di numero atomico 4, peso atomico 9,0122 fu individuato |
 |
 |
Il legame che tiene uniti gli atomi metallici all'interno del solido è detto legame metallico.
Tra i modelli più semplici ed intuitivi che descrivono il legame metallico vi è quello di P.Drude (1863-1906), secondo il quale gli atomi metallici perdono facilmente gli elettroni superficiali trasformandosi in ioni positivi. Gli ioni si accatastano in modo da lasciare il minor spazio vuoto possibile (massimo impaccamento), andando così ad occupare posizioni ben determinate all'interno di precise strutture geometriche. Gli elettroni persi non appartengono più ai singoli atomi, ma a tutto il reticolo solido (modello a mare di elettroni). Essi sono liberi di muoversi (elettroni delocalizzati) tra gli ioni positivi garantendo la neutralità del sistema e agendo da collante per i cationi.
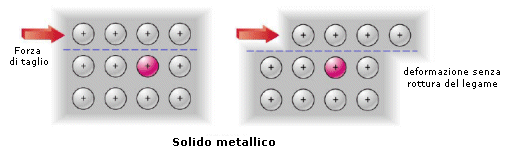
La libertà di movimento degli elettroni all'interno del reticolato cationico fa sì che il legame metallico manifesti una natura non direzionale. Non vi sono elettroni localizzati, come nel legame covalente, che irrigidiscono la struttura. Gli stessi cationi possono, se sollecitati meccanicamente, muoversi all'interno del mare di elettroni senza che il legame venga spezzato, a differenza di quanto accade in un legame ionico in cui anioni e catoni devono mantenere le loro posizioni reciproche. .Il legame metallico è adirezionale. Ciò spiega le caratteristiche di duttilità e malleabilità dei metalli i quali, se sottoposti a sollecitazioni meccaniche, si deformano in modo permanente senza spezzarsi.
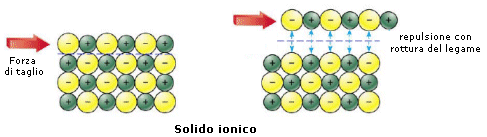
Se ad esempio sottoponiamo un solido metallico ed un solido ionico ad una forza di taglio che faccia slittare reciprocamente un piano di atomi rispetto ad un altro, possiamo notare che:
il legame metallico si conserva. La posizione che assumono i cationi nel mare di elettroni è infatti indifferente rispetto all'efficacia del legame
il legame ionico viene spezzato. Anioni e cationi vengono infatti a trovarsi di fronte a cariche dello stesso segno e si respingono.
Questo modello di legame giustifica una struttura costituita da un denso reticolato di ioni positivi molto vicini tra loro secondo il principio del massimo impaccamento. Il numero di atomi adiacenti a ciascun atomo è detto numero di coordinazione (N.C.) e per i metalli è molto elevato, tipicamente 8 o 12. Per questo motivo la densità dei metalli è generalmente superiore a quella degli altri materiali.
La disposizione degli atomi metallici all'interno del reticolo cristallino può essere di tipo compatto o di tipo non-compatto.
Le disposizioni di tipo compatto sono le più frequenti (90%) e si basano su stratificazioni di atomi con distribuzione esagonale.

distribuzione esagonale
Vanno a formare reticoli cristallini con elevato numero di coordinazione (12):
reticolo cubico a facce centrate (CFC)
reticolo esagonale compatto (EC).
Le disposizioni di tipo non-compatto si basano su stratificazioni di atomi con distribuzione quadrata.

distribuzione quadrata
Vanno a formare reticoli cristallini con numero di coordinazione inferiore:
reticolo cubico semplice (CS) o cubico primitivo (CP) con numero di coordinazione 6
reticolo cubico a corpo centrato (CCC) con numero di coordinazione 8
I diversi reticoli cristallini vengono descritti mediante l'individuazione di un elemento geometrico di base, detto cella elementare o cella unitaria, che si ripete al loro interno.
In un modello a sfere rigide lo spazio occupato dagli atomi all'interno di un reticolato cristallino viene misurato dal fattore di compattazione atomica o coefficiente di impaccamento definito dal rapporto tra il volume degli atomi contenuti in una cella unitaria del reticolo ed il volume della cella.
Reticolo Cubico Semplice o Cubico Primitivo - CS (sc - simple cubic packing)
La cella unitaria è costituita da otto atomi ai vertici di un cubo.

Ciascuno degli 8 atomi che si trovano ai vertici della cella è però condiviso da altre sette celle e appartiene quindi a ciascuna di esse per 1/8. In totale ogni cella contiene quindi un numero di atomi equivalenti pari a 8·1/8 = 1.

La distribuzione avviene per strati di sfere con disposizione quadrata. Le sfere del secondo strato giacciono esattamente sopra le sfere del primo strato. In questo modo ciascuna sfera è in contatto con altre sei sfere ed il numero di coordinazione è 6.
Si tratta di un reticolo estremamente raro nei metalli che compare solo nel Polonio.
Lo spigolo della cella elementare è detto costante reticolare a (o parametro di cella).
La distanza tra due atomi in contatto corriponde a 2r (due volte il raggio atomico) ed è uguale in questo caso al parametro di cella a. Poiché infatti vi sono 2 atomi a contatto lungo un lato della cella cubica, la costante reticolare è pari a 2 volte il raggio atomico
a = 2r
Il volume della cella elementare in funzione del raggio atomico r è quindi
![]()
Il coefficiente di impaccamento (fattore di compattazione atomica) si ottiene come rapporto tra il volume degli atomi equivalenti (sfere contenute nella cella elementare, in questo caso 1) ed il volume della cella elementare.
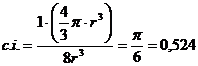
|
Reticolo cubico semplice |
|
|
Esempi |
Po |
|
Numero di atomi per cella elementare |
1 |
|
Numero di coordinazione |
6 |
|
Distanza tra atomi più vicini |
a |
|
Coefficiente di impaccamento |
p |
|
Dimensione della cella (costante reticolare a) |
2r |
Reticolo Cubico a Corpo Centrato - CCC (bcc - body centered cubic)
La cella unitaria è costituita da un atomo al centro di essa e da otto atomi ai vertici.

In questo modo gli atomi ai vertici non sono in contatto tra loro. Viceversa sono in contatto gli atomi sulla diagonale del corpo della cella nella sequenza "vertice-centro cella-vertice".
L'atomo centrale è dunque in contatto con 8 sfere ed il numero di coordinazione è 8
Ciascuno degli 8 atomi che si trovano ai vertici della cella è però condiviso da altre sette celle e appartiene quindi a ciascuna di esse per 1/8. In totale ogni cella contiene quindi un numero di atomi equivalenti pari a 1 + 8·1/8 = 2.
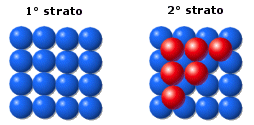
La distribuzione avviene per strati di sfere con disposizione quadrata. Le sfere del secondo strato giacciono nelle depressioni create dal primo strato, mentre le sfere del terzo strato giacciono nelle depressioni create dal secondo strato in modo da trovarsi esattamente sopra le sfere del primo strato
Lo spigolo della cella elementare è detto costante reticolare a.
Poiché vi sono 3 atomi a contatto lungo la diagonale D della cella cubica, la diagonale è pari a 4 volte il raggio atomico
D = 4r
Ricordando che in un cubo la diagonale è pari
D = a
con a = spigolo del cubo, la relazione tra il raggio atomico r e la costante reticolare a diventa
![]()
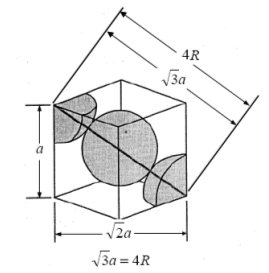
La minima distanza tra due atomi (2r) vale quindi (a · 3) / 2 = 0,866 a
Il volume della cella elementare in funzione del raggio atomico r è
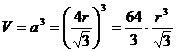
Il coefficiente di impaccamento (fattore di compattazione atomica) si ottiene come rapporto tra il volume degli atomi equivalenti (sfere contenute nella cella elementare, in questo caso 2) ed il volume della cella elementare.
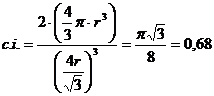
|
Reticolo cubico a corpo centrato |
|
|
Esempi |
Fe-a (a = 2,861Å), Cr (a = 2,878Å), Na (a = 4,240Å) |
|
Numero di atomi per cella elementare |
2 |
|
Numero di coordinazione |
8 |
|
Distanza tra atomi più vicini |
a · 3 / 2 = 0,866 · a |
|
Coefficiente di impaccamento |
p |
|
Dimensione della cella (costante reticolare a) |
(4/ 3)r |
Esempio
Il tungsteno (W) presenta una struttura cubica a corpo centrato. Calcoliamo la sua densità sapendo che il suo raggio atomico è 137 pm ed il suo peso molare è 183,84 g/mol
La densità del tungsteno può essere calcolata come rapporto tra la massa degli atomi contenuti in una cella ed il volume della cella. In una cella cubica a corpo centrato sono contenuti 2 atomi la cui massa è pari a
![]()
Per una cella cubica a corpo centrato la relazione tra le dimensioni dello spigolo a della cella ed il raggio r dell'elemento è
a = r (4/ 3) = 1,37 10-8 x ((4/ 3) = 3,164 10-8 cm
ed il volume della cella sarà
Vcella = a3 = (3,164 10-8)3 = 3.167 10-23 cm3.
La densità del Tungsteno sarà dunque
![]() g/cm3
g/cm3
Reticolo Cubico a Facce Centrate - CFC (fcc - face centered cubic)
Detto anche cubico compatto (CC). Nessun atomo giace interamente all'interno della cella unitaria ma vi sono 8 atomi ai vertici e 6 atomi al centro di ognuna delle facce.
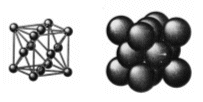
Così che ciascun atomo delle 6 facce è condiviso anche da un'altra cella e conta per 1/2 (contenuto in atomi = 6 x 1/2 = 3), mentre gli otto atomi ai vertici, come nella cella CCC, contano per 1/8 (8 x 1/8 = 1) Quindi in totale vi sono 4 atomi equivalenti per cella.

In questa cella gli atomi lungo la diagonale del cubo non sono in contatto tra loro. Viceversa sono in contatto gli atomi lungo la diagonale delle facce nella sequenza "vertice-centro faccia-vertice".
La distribuzione avviene per strati sovrapposti di sfere con disposizione esagonale. Le sfere del secondo strato giacciono nelle depressioni create dal primo strato, mentre le sfere del terzo strato giacciono nelle depressioni create dal secondo strato, non sopra le sfere del primo strato, ma in corrispondenza delle depressioni del primo strato non occupate dalle sfere del secondo strato.
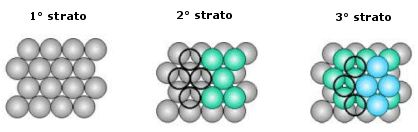
Solo le sfere del quarto stato si posizionano nelle depressioni del terzo in modo da sovrapporsi esattamente alle sfere del primo strato. Ne deriva una successione di strati esagonali di tipo ABCA..
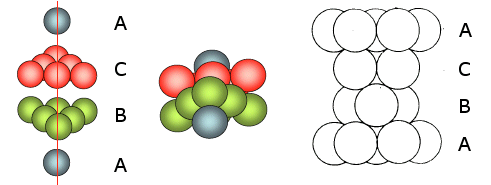
In questa cella sono in contatto 3 atomi lungo la diagonale DF della faccia del cubo,
DF = 4r
Ricordando che in un cubo la diagonale di una faccia è pari
DF = a
con a = spigolo del cubo, la relazione tra il raggio atomico r e la costante reticolare a diventa
![]()

La minima distanza tra due atomi (2r) vale quindi (a · 2) / 2 = 0,707 a
Il volume della cella elementare in funzione del raggio atomico r è
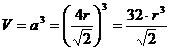
Il coefficiente di impaccamento (fattore di compattazione atomica) si ottiene come rapporto tra il volume degli atomi equivalenti (sfere contenute nella cella elementare, in questo caso 4) ed il volume della cella elementare.
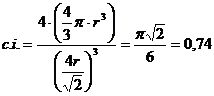
Il numero di coordinazione è il massimo raggiungibile con atomi dello stesso raggio e vale 12. La percentuale di spazio occupata è la più grande possibile in una struttura cristallina ad arriva al 74%, eguagliata soltanto da quella ottenibile nell'impaccamento esagonale compatto, come quello del titanio metallico.
|
Reticolo cubico a facce centrate |
|
|
Esempi |
Fe-g (a = 3,601), Ag (a = 4,078Å), Al (a = 4,041Å), Cu (a = 3,608 Å) |
|
Numero di atomi per cella elementare |
4 |
|
Numero di coordinazione |
12 |
|
Distanza tra atomi più vicini |
a · 2 / 2 = 0,707 · a |
|
Coefficiente di impaccamento |
p |
|
Dimensione della cella (costante reticolare a) |
(4/ 2)r |
Reticolo Esagonale Compatto - EC (hcp - Hexagonal closest packing)
12 atomi sono disposti ai vertici di un prisma a base esagonale, 2 atomi al centro di ciascuna base e 3 atomi all'interno della cella, a metà altezza, a formare i vertici di un triangolo equilatero

Ciascun atomo è circondato da altri 12 atomi
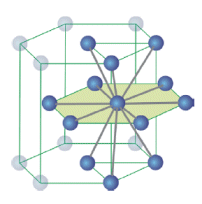
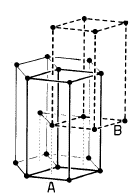
Le sfere del secondo strato giacciono nelle depressioni create dal primo strato, mentre le sfere del terzo strato giacciono nelle depressioni create dal secondo strato in modo da trovarsi esattamente sopra le sfere del primo strato
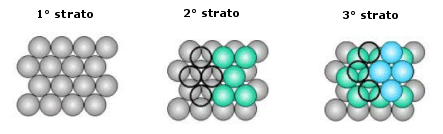
Ne deriva una successione di strati esagonali di tipo ABA
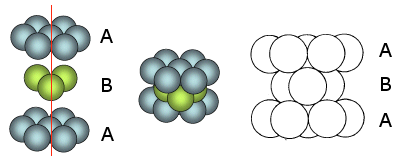
Il reticolo esagonale compatto è caratterizzato da un cella elementare prismatica esagonale che contiene 12 atomi posizionati ai vertici, 2 atomi posizionati al centro delle basi e 3 atomi ai vertici di un triangolo equilatero posizionati a metà altezza all'interno della cella elementare.
I 3 atomi interni appartengono completamente alla cella elementare. Ciascuno dei 12 atomi ai vertici è condiviso con altre 5 celle e quindi conta per 1/6 (contenuto in atomi = 12 x 1/6 = 2), mentre ciascuno dei due atomi posizionati al centro delle basi è condiviso con un'altra cella e conta per ½ (2 x 1/2 = 1) Quindi in totale vi sono 6 atomi equivalenti per cella.
Il lato dell'esagono di base costituisce la costante reticolare a ed essendo costituito da due sfere a contatto vale
a = 2r
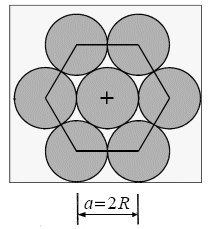
Calcoliamo ora il volume del prisma esagonale in funzione del raggio atomico r.
Consideriamo il sito tetraedrico costituito da 2 sfere poste su due vertici della base, dalla sfera posta al centro della base e da una sfera posta all'interno del tetraedro.
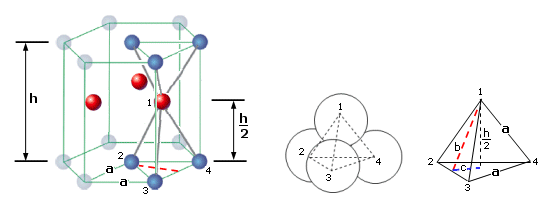
Il tetraedro ha un'altezza h/2 pari alla metà dell'altezza h del prisma ed è formato da 4 facce equilatere di lato a. L'altezza b di una faccia (triangolo equilatero) del tetraedro coincide con l'apotema dell'esagono di base del prisma e vale
b = (a ·
L'altezza del tetraedro è
h/2 = (a ·
e quindi l'altezza del prisma vale
h = (2a ·
L'area di base A del prisma è
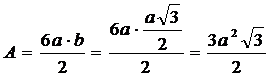
Il volume V del prisma
![]()
e, poiché a = 2r, il volume V, espresso in funzione del raggio atomico r, diventa
![]()
Il coefficiente di impaccamento (fattore di compattazione atomica) si ottiene come rapporto tra il volume degli atomi equivalenti (sfere contenute nella cella elementare, in questo caso 6) ed il volume della cella elementare.

|
Reticolo esagonale compatto |
|
|
Esempi |
Ti, Zn, Mg, Be |
|
Numero di atomi per cella elementare |
6 (cella a base esagonale) |
|
Numero di coordinazione |
12 |
|
Distanza tra atomi più vicini |
a |
|
Coefficiente di impaccamento |
p |
Esempio
Sapendo che il Titanio (d = 4,507 g/cm3 - PM = 47,867 g/mol) presenta una struttura esagonale compatta, calcoliamo il suo raggio atomico
Il volume della cella elementare può essere calcolato facendo il rapporto tra la massa di 6 atomi di Titanio (presenti nella sua cella elementare) e la densità del Titanio.
Calcoliamo la massa di 6 atomi di Titanio
![]()
Calcoliamo il Volume della cella elementare
![]()
Ricordando che il volume di una cella esagonale compatta in funzione del raggio atomico vale
![]()
possiamo ora calcolare il raggio atomico
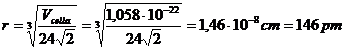
Raggio metallico
Il raggio metallico viene spesso definito come la metà della distanza che separa i nuclei di atomi adiacenti nel solido a temperatura e a pressione ambiente.
Tuttavia tale distanza dipende dal numero di coordinazione e generalmente, cresce con esso, come si osserva studiando i polimorfi dei metalli (metalli che cristallizzano con diverse celle elementari) e i composti intermetallici (Goldschmidt)
Per confrontare i vari elementi si corregge la distanza ínternucleare empirica riportandola al valore prevedibile per l'elemento in un ipotetico impacchettamento compatto (numero di coordinazione. = 12) dividendo il raggio osservato per i seguenti fattori di correzione
|
Numero Coordinazione |
Fattore di correzione |
|
|
|
|
|
|
|
|
|
|
|
|
Ad esempio il raggio metallico del Sodio con N.C = 8 è 1.85 Å. Dividendo tale valore per 0,97 si ottiene 1,91 Å, il raggio che il Sodio avrebbe se fosse compatto.
I valori «corretti» di Goldschmidt sono quelli normalmente tabulati.
Modello a bande
Il modello di Drude è oggi sostituito da un modello quantistico del legame metallico che si deve a F.Bloch, ed e' conosciuto come modello a bande.
Il modello a bande è un'applicazione della Teoria dell'Orbitale Molecolare (MO) ai metalli.
Si consideri ad esempio la molecola Li2. Ciascun atomo di Litio presenta un orbitale atomico 2s semisaturo. La molecola forma pertanto due orbitali molecolari sigma: un orbitale legante (σ2s) saturo ed un orbitale antilegante (σ2s*) vuoto.
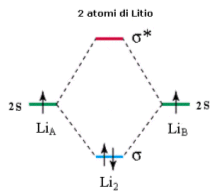
Si considerino ora 4 atomi di Litio legati. In questo caso si formeranno 2 orbitali di legame (σ2s) saturi e due orbitali di antilegame (σ2s*) vuoti. Questo sistema a 4 atomi è più stabile del precedente essendo caratterizzato da un maggior numero di orbitali di legame saturi.
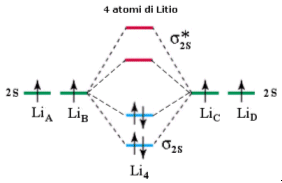
Se estendiamo il ragionamento ad n atomi otterremo un sistema costituito da n/2 orbitali di legame (σ2s) saturi ed n/2 orbitali di antilegame (σ2s*) vuoti. Gli orbitali di legame saturi e quelli di antilegame vuoti si dispongono su livelli energetici talmente vicini da formare una banda continua di energia.
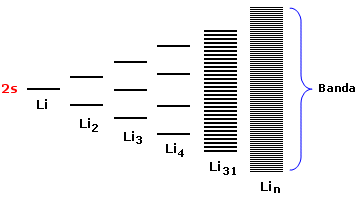
In altre parole all'interno di ciascuna banda le differenza energetiche tra gli orbitali molecolari sono così piccole che possiamo considerare la distribuzione energetica come non quantizzata.
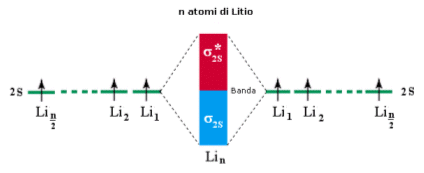
Come per il legame covalente, anche nel caso del legame metallico la forza del legame dipende dalla differenza tra il numero di elettroni negli orbitali leganti ed il numero di elettroni negli orbitali antileganti. Quanti più elettroni vi sono negli orbitali di legame rispetto agli orbitali di antilegame e tanto più il legame sarà intenso ed il metallo presenterà maggiore durezza e più elevato punto di fusione.
Questo significa che queste proprietà saranno massime al centro di un periodo di transizione. Per metalli con configurazione del tipo nd5 o adiacenti. In questo caso infatti, poiché ogni atomo ha i propri orbitali esterni semisaturi, gli orbitali molecolari leganti saranno completi, mentre quelli antileganti saranno vuoti. È una situazione analoga a quella del Litio, con la differenza che il numero di orbitali interessato al legame è notevolmente superiore.
Durezza e punto di fusione dei metalli hanno quindi un andamento periodico. Crescono dall'inizio fino al centro di una serie di transizione per poi decrescere proseguendo verso destra.

In un metallo la banda più esterna che contiene elettroni è detta banda di valenza Le bande possono essere separate da brevi intervalli energetici, dette zone proibite (band gap), in cui gli elettroni non possono essere presenti.
Il livello energetico più elevato occupato da elettroni (HOMO = Highest occupied molecular orbital) all'interno della banda di valenza alla temperatura dello zero assoluto è detto livello di Fermi (o energia di Fermi). Ad esempio per il Litio metallico il livello di Fermi si situa esattamente a metà della banda di valenza 2s.
Dunque a zero gradi kelvin gli elettroni del Litio, si trovano tutti ad energie minori dell'energia di Fermi, che si colloca a metà della banda 2s
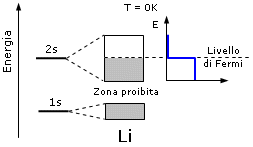
Ma a temperature superiori a zero kelvin gli elettroni, in quanto fermioni, obbedediscono alla distribuzione statistica di Fermi-Dirac. Anche per piccoli aumenti di temperatura, si rendono disponibili (nel senso statistico del termine) stati conduttivi, ossia elettroni che prima erano "congelati" nella metà inferiore della banda 2s, possono essere promossi ad energie più elevate e dunque risultano liberi di muoversi nel metallo e di condurre energia.
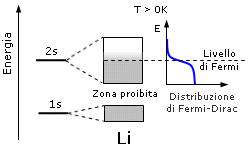
In un tale conduttore esistono stati liberi al di sopra del livello di Fermi e se si applica un campo elettrico gli elettroni si muovono nella direzione opposta al campo contribuendo a creare corrente. Al processo di conduzione non partecipano le bande di energia inferiore che sono totalmente occupate. Le bande ad energia inferiore, costituite dagli orbitali più interni e completamente sature, sono in genere poco estese e ben distanziate energeticamente (intervalli proibiti estesi). All'aumentare dell'energia le bande diventano più larghe e più ravvicinate fino, in alcuni casi, a sovrapporsi.
Nei metalli che, come il Litio, presentano la banda di valenza non completamente piena, banda di valenza e banda di conduzione coincidono.
In altre parole si tratta di considerare che, se un metallo presenta la banda di valenza non completamente piena di elettroni, essa è disponibile ad essere popolata da elettroni con energia sufficiente e diventare così una banda di conduzione. Questo meccanismo avviene tipicamente ad opera di schemi di eccitazione termica. Se una banda non è completamente piena, gli elettroni ad energia più alta possono facilmente essere promossi a stati di energia leggermente superiore, e contribuiscono significativamente alla conducibilità.
Questo accade per il Litio e per tutti i metalli che presentano una banda di valenza semisatura, ma è possibile anche per un metallo come il Berillio che, pur avendo la banda 2s completamente satura (sia quella di legame che quella di antilegame), presenta la banda 2s parzialmente sovrapposta alla banda 2p vuota che diventa dunque la banda di conduzione
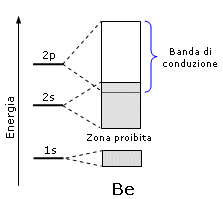
Presentano dunque un comportamento metallico gli elementi con:
la banda di valenza occupata solo parzialmente che funge da banda di conduzione
la banda di valenza satura parzialmente sovrapposta alla banda di conduzione vuota
La conducibilità dei metalli diminuisce all'aumentare della temperatura poiché l'aumento dei moti vibrazionali dagli atomi va ad interferire con il moto degli elettroni.
La facilità con cui gli elettroni di conduzione possono muoversi attraverso il reticolo metallico spiega anche la buona conducibilità termica dei metalli. Quando un metallo viene avvicinato ad una fonte di calore gli elettroni di conduzione aumentano la loro energie cinetica media che, data la loro mobilità può essere facilmente trasferita alle particelle adiacenti.
La lucentezza dei metalli si spiega infine con la vicinanza degli orbitali molecolari all'interno della banda di conduzione. In pratica gli elettroni, avendo a disposizione moltissimi livelli energetici adiacenti, possono facilmente esservi promossi assorbendo luce su tutte le lunghezze d'onda per poi riemetterla per tornare allo stato fondamentale.
La teoria delle bande, oltre a giustificare le caratteristiche metalliche è in grado di fornire una spiegazione semplice ed immediata dell'esistenza dei semiconduttori e degli isolanti.
Isolanti
Gli isolanti sono caratterizzati da un sistema di bande nel quale quella più alta occupata è completamente piena (banda di valenza) e quella successiva, completamente vuota (banda di conduzione), si trova separata da un intervallo proibito talmente esteso da non poter essere superato se non sottoponendo il materiale a differenze di potenziale estremamente elevate.
La caratteristica di un isolante è quindi quella di possedere una banda di valenza completamente satura separata dalla banda di conduzione vuota da un intervallo di energia proibito molto maggiore della tipica energia termica. In tali condizioni la temperatura non è in grado di promuovere un elettrone nella banda superiore che è vuota e dunque, in presenza di un campo elettrico, non si ha passaggio di coerente. Un tipico isolante è il diamante in cui l'intervallo di energia proibito è circa duecento volte l'energia termica a temperatura ambiente. Alcuni fisici separano gli isolanti dai semiconduttori ponendo arbitrariamente pari a 4 eV le dimensioni energetiche della zona proibita.
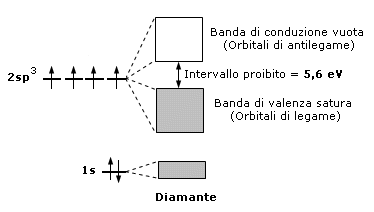
Semiconduttori
Sono semiconduttori elementi come il silicio ed il germanio che presentano una banda piena ed un intervallo di banda (zona proibita) con un valore non eccessivamente alto, tale comunque da poter essere superato fornendo adeguate quantità di energia al cristallo.
E' questo il motivo per cui nei semiconduttori la resistenza al passaggio di corrente elettrica diminuisce all'aumentare della temperatura. Le proprietà di semiconduttori o di isolanti dipendono quindi dall'intevallo (gap) tra la banda di valenza e quella di conduzione.
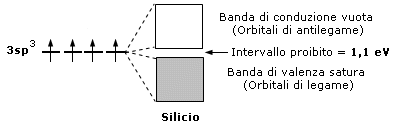
I semiconduttori hanno bassa conducibilità elettrica a temperatura ambiente, ma questa aumenta fortemente all'aumentare della temperatura. Il livello di Fermi si posiziona tipicamente tra la banda di valenza e quella di conduzione. All'aumentare della temperatura la distribuzione di Fermi-Dirac si modifica aumentando la probabilità che gli elettroni possiedano energia sufficiente a popolare la banda di conduzione.
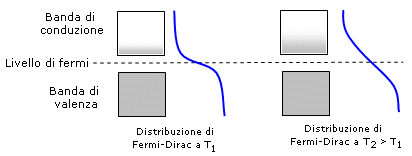
Semiconduttori con particolari caratteristiche si possono costruire attraverso il processo di drogatura, aggiungendo ad un semiconduttore piccole percentuali di impurezze. Ad esempio mescolando al silicio piccole, ma ben definite quantità di arsenico o di gallio.
La drogatura con arsenico è detta di tipo n (negativa) in quanto viene aggiunto un elemento chimico che presenta la stessa configurazione superficiale del silicio più un elettrone. Gli elettroni in più vanno a disporsi nella banda superiore e sono disponibili per la conduzione.
La drogatura con gallio viene detta di tipo p (positiva) in quanto viene aggiunto un elemento chimico che presenta la stessa configurazione superficiale del silicio meno un elettrone. Gli elettroni in meno creano delle lacune elettroniche nella banda più superficiale del silicio creando le premesse per la conduzione.
 |
| Appunti su: legame metallico, legame metallico riassunto, descrizione legame metallico in parole semplici, legame metallico drude, Punto di fusione dei metalli, |
|
| Appunti Biologia |  |
| Tesine Ingegneria tecnico |  |
| Lezioni Geografia |  |