 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 4870 | Gradito: |
Leggi anche appunti:La nomenclatura dei composti organiciLa nomenclatura dei composti organici I composti organici sono molti milioni. Esercitazione di chimicaESERCITAZIONE DI CHIMICA SCOPO DELL' ESPERIENZA: Estrazione e cromatografia Entalpia (H) e termochimicaEntalpia (H) e termochimica Dagli esempi visti finora sulle interazioni |
 |
 |
Il legame ionico è il legame che si realizza quando un atomo a bassa energia di ionizzazione si combina con un atomo ad elevata affinità elettronica. È il tipo più semplice di legame chimico ed è interpretabile in base alle leggi classiche dell'elettrostatica. Si assume un completo trasferimento di elettroni dall'atomo a bassa energia di ionizzazione all'atomo ad alta affinità elettronica. Il legame si produce come conseguenza dell'attrazione elettrostatica che si manifesta tra i due ioni di carica opposta che si formano.
Un esempio classico di legame ionico si ha nella formazione del Cloruro di Sodio a partire dal Sodio e dal Cloro elementari.
Nella reazione tra Sodio e Cloro, il Sodio metallico (configurazione superficiale 3s1) cede al Cloro (configurazione superficiale 3s23p5) il suo elettrone con formazione del Cloruro di Sodio, un composto ionico in cui gli ioni Na+ e gli ioni Cl- risultano uniti tramite legame ionico.
![]()
Il Sodio raggiunge in questo modo la configurazione stabile del gas nobile che lo precede (Elio), mentre il Cloro quella del gas nobile che lo segue (Argon).

Ricordiamo tuttavia che non esiste una singola molecola di Cloruro di Sodio, come abitualmente e convenzionalmente si scrive. L'attrazione tra cariche di segno opposto, come sono cationi ed anioni, non si sviluppa infatti solo in un'unica direzione, ma agisce uniformemente in tutte le direzioni con simmetria sferica producendo aggregati ionici macroscopici strutturati in cui anioni e cationi si alternano in un reticolo ordinato. Per questo motivo il legame ionico, a differenza del legame covalente, non è direzionale.
Il numero di anioni che circonda un catione all'interno del reticolo cristallino è detto numero di coordinazione del catione.
Il numero di cationi che circonda un anione all'interno del reticolo cristallino è detto numero di coordinazione dell'anione.
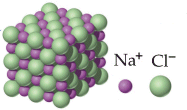
Nel Cloruro di Sodio, ad esempio, ogni ione Na+ risulta circondato da 6 ioni Cl- e viceversa., formando uno sconfinato reticolato cubico, in cui ioni di carica opposta si alternano ordinatamente nelle tre direzioni dello spazio. Tale disposizione ordinata è detta cristallina, poichè genera macroscopicamente un cristallo che conserva la geometria della sottostante struttura atomica.
Nei composti ionici dunque, come abbiamo già avuto modo di dire, la formula chimica non descrive una struttura molecolare autonoma, ma indica il rapporto numerico esistente nel cristallo tra ioni positivi e negativi (formula minima). Allo stesso modo è più corretto, riferendosi ai composti ionici, parlare di peso formula piuttosto che di peso molecolare.
Nel caso del Cloruro di Sodio, ad esempio, la formula NaCl ci informa che il rapporto numerico tra ioni Na+ e Cl- all'interno del reticolo è di 1:1.
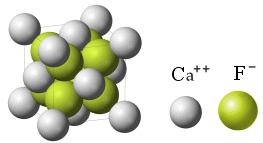
Se la reazione fosse avvenuta tra il Calcio ed il Fluoro, il Calcio avrebbe ceduto due elettroni a 2 atomi di Fluoro, ciascuno dei quali avrebbe acquistato un elettrone.
In tal caso, affinchè il reticolato ionico sia nel complesso neutro è necessario che per ciascun ione Ca2+ siano presenti 2 ioni F-.
La formula CaF2 indica dunque che nel reticolo cristallino del Fluoruro di Calcio (Fluorite) il rapporto tra ioni Calcio e ioni Fluoro è 2:1.
In un solido ionico si assume che la distanza tra gli ioni di carica opposta (distanza internucleare) sia uguale alla somma dei raggi ionici del catione e dell'anione. Le distanze internucleari possono essere misurate molto accuratamente con i metodi cristallografici, ma il problema è ovviamente stabilire quanto contribuisca il raggio di ciascun ione alla distanza totale misurata. In altre parole il problema è di assegnare a ciascun ione la sua frazione di distanza internucleare (il suo raggio ionico).
La determinazione dei raggi ionici si effettua in genere assumendo come noto il raggio ionico di uno ione e calcolando tutti gli altri per differenza.
Le prime misure di raggi ionici si devono a Pauling (1928), che assunse per lo ione ossido O2- un raggio ionico di 140 pm. L'anione O2- presenta il vantaggio di trovarsi combinato con moltissimi elementi e di essere accettabilmente non polarizzabile, per cui la sua dimensione non varia molto cambiando l'intorno.
|
Raggio Ionico (pm) - Pauling |
||||||||
|
Li+ |
Be2+ |
|
B3+ |
C |
N3- |
O2- |
F- |
|
|
Na+ |
Mg2+ |
Al3+ |
Si |
P3- |
S2- |
Cl- |
||
|
K+ |
Ca2+ |
Sc3+ |
Zn2+ |
Ga3+ |
Ge |
As3- |
Se2- |
Br- |
|
Rb+ |
Sr2+ |
Y3+ |
Cd2+ |
In3+ |
Sn |
Sb3- |
Te2- |
I- |
|
Cs+ |
Ba2+ |
La3+ |
Hg2+ |
Tl3+ |
Pb |
Bi |
Po |
At |
Successivamente Shannon e Prewitt (1969,1970) proposero valori oggi ritenuti più attendibili in cui i cationi sono significativamente più grandi e gli anioni più piccoli rispetto ai valori assegnati in precedenza.
I raggi ionici sono utili per prevedere la struttura geometrica del reticolato ionico, ma vanno usati con attenzione poiché, mescolando valori provenienti da fonti diverse, si può incorrere in grossolani errori.
Inoltre i raggi ionici non sono costanti per un certo ione, ma aumentano in genere all'aumentare del numero di ioni di carica opposta che lo circondano (numero di coordinazione). Il confronto dei raggi ionici richiede dunque l'uso di valori basati su un unico numero di coordinazione (in genere tipicamente 6).
Di seguito riportiamo i raggi ionici proposti da Shannon per il numero di coordinazione 6 (tra parentesi sono riportati eventuali numeri di coordinazione diversi)
|
Raggio Ionico (pm) - Shannon |
||||||||||||||||||
|
|
H+ |
|
He |
|||||||||||||||
|
|
Li+ |
Be2+ |
|
B3+ |
C4+ |
N3- |
O2- |
F- |
Ne |
|||||||||
|
|
Na+ |
Mg2+ |
|
Al3+ |
Si4+ |
P5+ |
S2- |
Cl- |
Ar |
|||||||||
|
|
K+ |
Ca2+ |
Sc3+ |
Ti4+ |
V5+ |
Cr6+ |
Mn7+ |
Fe3+ |
Co3+ |
Ni3+ |
Cu2+ |
Zn2+ |
Ga3+ |
Ge4+ |
As5+ |
Se2- |
Br- |
Kr |
|
|
Rb+ |
Sr2+ |
Y3+ |
Zr4+ |
Nb5+ |
Mo6+ |
Tc7+ |
Ru3+ |
Rh3+ |
Pd2+ |
Ag+ |
Cd2+ |
In3+ |
Sn4+ |
Sb3+ |
Te2- |
I- |
Xe |
|
|
Cs+ |
Ba2+ |
La3+ |
Hf4+ |
Ta5+ |
W6+ |
Re7+ |
Os4+ |
Ir4+ |
Pt4+ |
Au3+ |
Hg2+ |
Tl3+ |
Pb4+ |
Bi3+ |
Po4+ |
At |
Rn |
|
|
Fr+ |
Ra2+ |
Ac |
Rf |
Db |
Sg |
Bh |
Hs |
Mt |
Ds |
Rg |
Uub |
Uut |
Uuq |
Uup |
Uuh |
Uus |
Uuo |
Il numero di ioni di carica opposta che circondano un dato ione dipende da fattori geometrici secondo il principio del massimo impaccamento. In altre parole la geometria di un composto ionico è quella che rende minima l'energia del sistema, per cui ogni ione deve essere circondato dal massimo numero di ioni di segno opposto e la distanza tra ione positivo e ione negativo deve essere la minima possibile. L'impaccamento si produce come se gli ioni fossero sfere rigide che si sistemano in modo da rendere minimi gli spazi vuoti tra una sfera e l'altra (in effetti gli ioni non si comportano come sfere rigide, ma si deformano (polarizzazione) in funzione delle forze elettrostatiche di attrazione e repulsione).
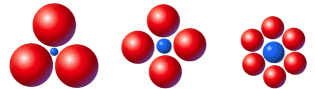
Tipi di coordinazione planare tra ioni con rapporti di raggi ionici diversi.
Il numero massimo di anioni che è possibile porre a contatto con un catione (numero di coordinazione del catione) e quindi il tipo di impaccamento e di reticolato geometrico dipende sostanzialmente dalle dimensioni relative degli ioni positivi e negativi. Più esattamente, dipende dal rapporto fra il raggio dello ione più piccolo (in genere il catione) ed il raggio dello ione più grande (in genere l'anione) o rapporto radiale (Rr = r+/r-).
|
Numero di Coordinazione (NC) |
Rapporto radiale (Rr = r+/ r-) |
Geometria di coordinazione |
|
|
Rr < 0,155 |
Lineare |
|
|
Rr < 0,224 |
Trigonale |
|
|
Rr < 0.414 |
Tetraedrica |
|
|
Rr < 0,732 |
Ottaedrica |
|
|
Rr < 1 |
Cubica |
|
|
Rr = 1 |
Cubo-ottaedrica |
Ad esempio, nel Cloruro di Cesio il rapporto radiale tra il raggio ionico di Cs+ e quello di Cl- vale rCs+/rCl- = 167/181 = 0,923. Il cesio presenterà dunque un numero di coordinazione NC = 8 ed una geometria cubica
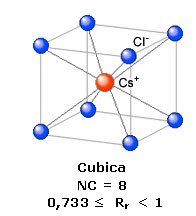
Ogni ione Cs+ è circondato da 8 ioni Cl- e, poiché il rapporto ionico e 1:1, anche ogni ione Cl- sarà circondato da 8 ioni Cs+
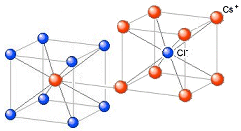
Nel Fluoruro di Calcio (CaF2 Fluorite) il rapporto radiale tra il raggio ionico di Ca2+ e quello di F- vale rCa2+/rF- = 100/133 = 0,75. Il Ca2+ presenterà dunque un numero di coordinazione NC = 8 ed una geometria cubica a facce centrate.
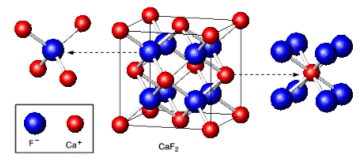
Ogni ione Ca2+ è circondato da 8 ioni F- disposti al vertice di un ottaedro. Ma, poiché il rapporto ionico e 1:2, ogni ione F- sarà circondato da 4 ioni Ca2+ disposti ai vertici di un tetraedro
Nel Cloruro di Sodio (NaCl) il rapporto radiale tra il raggio ionico di Na+ e quello di Cl- vale rCa+/rCl- = 102/181 = 0,56. Il Na+ presenterà dunque un numero di coordinazione NC = 6 ed una geometria ottaedrica.
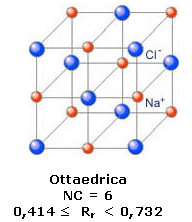
Ogni ione Na+ è circondato da 6 ioni Cl- disposti al vertice di un ottaedro e, poiché il rapporto ionico e 1:1, anche ogni ione Cl- sarà circondato da 6 ioni Na+ disposti al vertice di un ottaedro
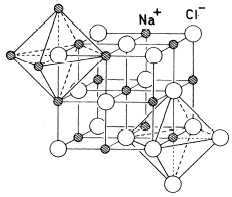
Per sapere perché le sostanze ioniche formino cristalli e non si limitino a costituire coppie ioniche isolate, occorre fare alcune considerazioni energetiche sui legami ionici.
Consideriamo allora il legame ionico dal punto di vista energetico, analizzando ancora una volta la reazione di sintesi del Cloruro di Sodio.
2Na(s) + Cl2(g) → 2 NaCl(s) + 196,6 kcal
L'energia che si libera durante la formazione del legame è pari a 96,3 kcal per mole di NaCl (Entalpia di formazione ΔHf = -96,3 kcal/mol). Evidentemente trasformandosi in ioni entrambi gli atomi hanno raggiunto una configurazione più stabile ed hanno diminuito il loro contenuto energetico.
Tuttavia se confrontiamo semplicemente le variazioni di energia associate alla formazione degli ioni, il processo non sembra energeticamente favorito.
Il Sodio presenta una energia di ionizzazione molto bassa
Na(g) + 118,5 kcal/mol → Na+(g) + e-
mentre il Cloro ha una Affinità elettronica molto elevata
Cl(g) + e- → Cl-(g) + 83,4 kcal/mol
In effetti, sommando l'Energia di ionizzazione del Sodio e l'energia di Affinità elettronica del Cloro, il processo di formazione del legame ionico non sembrerebbe favorito, richiedendo 35,1 kcal
Na(g) + 118,5 kcal → Na+(g) + e- +
Cl(g) + e- → Cl-(g) + 83,4 kcal =
![]()
Na(g) + Cl(g) + 35,1 kcal → Na+(g) + Cl-(g)
Il fatto è che la reazione precedente non descrive la formazione del cloruro di sodio, ma quella dei suoi ioni allo stato gassoso, idealmente posti a distanza infinita l'uno dall'altro. Il processo di avvicinamento degli ioni, sotto l'azione delle reciproche forze di attrazione, fino a formare il composto ionico fa notevolmente diminuire l'energia del sistema.
Si definisce energia reticolare l'energia liberata nella formazione del reticolo cristallino dagli ioni componenti allo stato gassoso portati da distanza infinita a distanza di legame.
L'energia reticolare dipende da diversi fattori, ma in particolare dalla densità di carica (q/r = rapporto carica/raggio). Più elevata è la densità di carica maggiore è l'energia reticolare.
|
|
|
Li+ |
Na+ |
K+ |
Rb+ |
Cs+ |
|
Be2+ |
Mg2+ |
Ca2+ |
Sr2+ |
Ba2+ |
|
|
q/r |
|
|
|
|
|
|
|
|
|
|
|
|
F- |
|
|
|
|
|
|
|
|
|
|
|
|
|
Cl- |
|
|
|
|
|
|
|
|
|
|
|
|
|
Br- |
|
|
|
|
|
|
|
|
|
|
|
|
|
I- |
|
|
|
|
|
|
|
|
|
|
|
|
Densità di carica (q/r) ed energia reticolare (kJ mol-1) misurata e calcolata (tra parentesi)
per gli alogenuri dei metalli alcalini ed alcalino-terrosi
Tuttavia va tenuto presente che se il catione è troppo piccolo (densità di carica eccessivamente elevata) esso non riesce ad inserirsi efficacemente nel reticolo cristallino poiché gli anioni verrebbero a contatto, e tenderà pertanto a stabilizzarsi tramite legami covalenti. Così ad esempio gli elementi del II gruppo formano tutti composti ionici ad eccezione del Be2+ (troppo piccolo). Così non sono noti composti ionici del B3+ e del C4+.
L'energia reticolare risulta essenzialmente data dalla combinazione di due termini opposti la repulsione tra i gusci elettronici (energia di repulsione elettronica) e l'attrazione tra ioni di carica opposta (energia di Madelung).
Quando idealmente gli ioni di carica opposta si avvicinano, l'energia reticolare diminuisce fino ad arrivare ad un valore minimo per una distanza tra gli ioni pari alla somma dei loro raggi ionici.
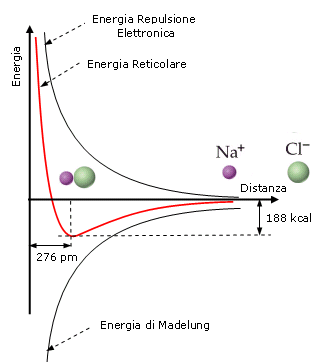
Nel caso del Cloruro di Sodio, ad esempio, l'energia reticolare è pari a 188 kcal/mol in corrispondenza ad una distanza interionica di 276 pm (picometri) = 181 pm (raggio ionico Cl-) + 95 pm (raggio ionico Na+).
Per valutare l'entità dell'energia reticolare di un cristallo di Cloruro di Sodio, iniziamo a calcolare l'energia potenziale coulombiana di una coppia ionica gassosa di NaCl. Studiando la molecola di cloruro di sodio biatomica gassosa, si è trovato che la sua distanza internucleare è 2,38 Å, per cui l'energia potenziale coulombiana è
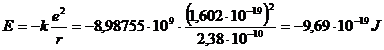
per ottenere l'energia di una mole di coppie ioniche è necessario moltiplicare il risultato precedente per il numero di Avogadro
-9,69·10-19 x 6.022·1023 = -583,6 kJ mol-1 = -139,6 kcal mol-1
Ora, per trovare l'energia di formazione sviluppata quando un cristallo di cloruro di sodio si forma dagli ioni gassosi, si deve calcolare l'energia potenziale coulombiana di uno ione quando esso è sotto l'azione di tutti gli altri ioni del cristallo. A tal fine consideriamo il modello semplificato monodimensionale seguente e calcoliamo l'energia coulombiana degli ioni rispetto allo ione sodio centrale
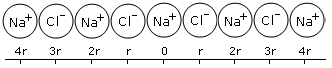
I primi due ioni di cloro vicini, disposti ad una distanza r, contribuiranno all'energia potenziale con un valore pari a -2ke2/r , mentre i successivi due ioni sodio contribuiranno con +2ke2/2r (il segno positivo deriva dalla repulsione tra le cariche eguali sugli ioni di sodio).
Continuando il ragionamento si ha:
![]()
Come si può osservare, l'espressione dell'energia totale è data da uno sviluppo in serie in cui il valore di ogni addendo dipende dalla carica degli ioni che interagiscono e dalla posizione che questi occupano nel reticolo, mentre è indipendente dalla natura chimica degli ioni che effettivamente occupano le posizioni.
Lo sviluppo in serie è costituito da una sequenza di addendi alternativamente negativi e positivi ma di entità sempre più piccola, che converge verso un valore numerico M maggiore di 1, detto Costante di Madelung, indipendente dal valore di r.
La costante di Madelung dipende dunque solo dal tipo di reticolo e dalla mutua posizione geometrica dei singoli ioni.
|
Esempio |
Numero di coordinazione dei cationi |
Numero di coordinazione degli anioni |
Costante di Madelung |
|
NaCl |
|
|
|
|
CsCl |
|
|
|
|
ZnS (wurtzite) |
|
|
|
|
ZnS (blenda) |
|
|
|
|
CaF2 (fluorite) |
|
|
|
|
TiO2 (rutilo) |
|
|
|
Poiché la costante di Madelung è sempre maggiore di uno, l'energia di attrazione elettrostatica globale è di conseguenza sempre maggiore (in valore assoluto) nel reticolo rispetto al caso di una singola coppia ionica.
Questa energia, che si ottiene moltiplicando l'energia di interazione della coppia per la costante di Madelung relativa, con le debite correzioni, si chiama Energia di Madelung, principale responsabile della stabilità dei cristalli delle sostanze ioniche. Se essa non ci fosse, esisterebbero solo coppie ioniche isolate.
Per il reticolo cristallino del cloruro di sodio è M = 1,75, per cui, a parità di tutte le altre condizioni, il solido ionico ha un'energia che è il 75% più bassa di quella della molecola biatomica gassosa. Questo ulteriore abbassamento di energia si verifica perché uno ione sodio nel solido è legato mediante forze coulombiane a tutti gli ioni nel cristallo.
Essendo la distanza tra gli ioni nel cristallo del cloruro di sodio pari a 2,76 Å (maggiore che nella molecola biatomica) si ha
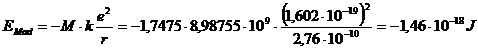
per ottenere l'energia di Madelung di una mole è necessario moltiplicare il risultato precedente per il numero di Avogadro
-1,46·10-18 x 6.022·1023 = -879,5 kJ mol-1 = -210,4 kcal mol-1
Per calcolare l'energia reticolare è ora necessario stimare anche l'energia repulsiva che si genera tra le nuvole elettroniche degli ioni quando questi si trovano a piccole distanze.
Eret = EMad + Erep
Tale repulsione è della stessa natura delle repulsioni di van der Waals fra gli atomi neutri di cui ci occuperemo nel prossimo capitolo ed ha una dipendenza dalla distanza interatomica r del tipo
![]()
con
n > 6 (con valori caratteristici 9, 12 o 14 in relazione al tipo di ioni. Spesso n può essere calcolato studiando la compressibilità del cristallo)
B = coefficiente caratteristico del solido ionico
L'espressione dell'energia reticolare diventa dunque
![]()
Tuttavia B può essere eliminato dall'espressione dell'energia reticolare considerando che al valore di r in cui il cristallo è più stabile (r di legame) l'energia reticolare assume il suo valore minimo (pendenza nulla e derivata della funzione uguale a zero dE/dr=0).
![]()
da cui
![]()
che, sostituita nella relazione dell'Energia reticolare, fornisce
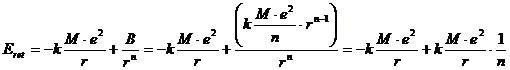
Dunque, poiché n 10, l'energia di repulsione risulta circa 1/10 dell'energia di Madelung e quindi, per il cloruro di sodio
Eret = EMad + Erep = -210,4 + 21,04 = 189 kcal mol-1
Il valore sperimentale dell'energia reticolare per NaCl è di 188 kcal mol-1
L'energia reticolare può essere sperimentalmente determinata tramite un ciclo di Born-Haber, in cui il processo di formazione del legame ionico viene spezzato in una serie di fasi che trasformano i reagenti negli ioni gassosi e successivamente gli ioni gassosi nel solido ionico.
Vaporizzazione del Sodio (Energia di vaporizzazione)
Na(s) + ½ Cl2(g) + 26 kcal → Na(g) + ½ Cl2(g)
Dissociazione del Cloro (½ dell'energia di legame Cl-Cl)
Na(g) + ½ Cl-Cl(g) + 28,6 kcal → Na(g) + Cl.(g)
Ionizzazione del Sodio (Energia di Ionizzazione)
Na(g) + Cl.(g) + 118,5 kcal → Na+(g) + Cl.(g) + e
Ionizzazione del Cloro (Energia di Affinità elettronica)
Na+(g) + Cl.(g) + e → Na+(g) + Cl+(g) + 83.4 kcal
Formazione legame a partire dagli elementi gassosi (Energia reticolare)
Na+(g) + Cl+ (g) → NaCl(s) + 188 kcal
Sommando membro a membro le 5 reazioni precedenti si ottiene la reazione di formazione del Cloruro di Sodio a partire dai suoi elementi e la relativa Energia di formazione
Na(s) + ½ Cl2(g) → NaCl(s) + 98,3 kcal
I diversi stadi vengono spesso schematicamente rappresentati attraverso il cosiddetto ciclo di Born-Haber, dove, secondo la convenzione, le energie assorbite hanno segno positivo, quelle cedute segno negativo
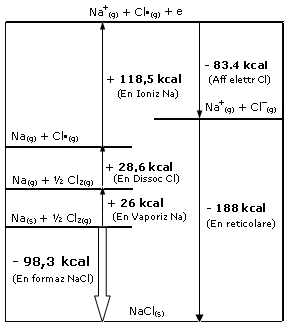
Come si può osservare, nella formazione di sostanze ioniche è particolarmente importante il confronto tra l'energia di ionizzazione e l'energia reticolare, trattandosi dei due termini energetici più rilevanti. In prima approssimazione un composto ionico si formerà se l'energia spesa per la ionizzazione verrà compensata dall'energia reticolare. Ad esempio, il composto ionico MgCl con Mg+ non si osserva, nonostante lo ione Mg+ richieda meno energia per formarsi rispetto allo ione Mg2+ (Mg = Mg+ + e + 738 kJ mol-1 contro Mg+ = Mg2+ + e + 1450 kj mol-1). Ciò è dovuto al fatto che l'energia reticolare di MgCl è troppo piccola.
 |
| Appunti su: energia reticolare chimica, energia reticolare, legame ionico, raggi ionici shannon cristalli, |
|
| Appunti Biologia |  |
| Tesine Geografia |  |
| Lezioni Ingegneria tecnico |  |