 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2663 | Gradito: |
Leggi anche appunti:Reattività degli addotti MX2(N,N'-C12H6N2O2); M = Co,Fe, X = Cl; M = Ni, X = BrReattività degli addotti MX2(N,N'-C12H6N2O2); M = Co,Fe, X = Cl; M = Ni, X = Br. 1.1.1. Reazione Il modello atomico di BohrIl modello atomico di Bohr Preso in considerazione l'atomo di Idrogeno, Bohr Limiti di applicabilità della relazione di Henderson-HasselbachLimiti di applicabilità della relazione di Henderson-Hasselbach Nell'equazione |
 |
 |
Nella seconda metà dell'Ottocento Maxwell e Boltzmann riuscirono a formulare una descrizione coerente del comportamento della materia e dell'energia applicando una teoria chiamata Meccanica Statistica.
Il presupposto alla base della meccanica statistica è che, essendo i sistemi materiali composti da un numero enorme di elementi (atomi o molecole), non è possibile , per ragioni pratiche, applicare alle singole particelle le leggi della meccanica classica, calcolando per ciascuna la posizione, la velocità e l'energia di ciascuna particella. Pur tuttavia rimane possibile descrivere tali sistemi prendendo in considerazione i valori medi che assumono le variabili dinamiche e cinematiche in gioco.
In altre parole tale teoria è una descrizione statistica delle proprietà dinamiche e cinematiche degli aggregati di particelle che costituiscono un sistema materiale.
La meccanica statistica è giunta per tale via ad ottenere risultati di grande rilievo, riuscendo a dimostrare che le variabili macroscopiche che descrivono lo stato esteriore della materia, come il volume, la pressione e la temperatura sono collegabili alle variabili microscopiche che descrivono il comportamento dinamico delle singole particelle, come l'energia cinetica media, la frequenza degli urti tra particelle etc.
Quella parte della meccanica statistica che descrive il moto disordinato delle particelle gassose viene comunemente indicata come teoria cinetica dei gas.
La teoria cinetica si applica ai gas perfetti e vale quindi solo se sono rispettate le seguenti condizioni:
1) Il volume delle particelle (covolume) è trascurabile rispetto al volume del gas.
2) Le forze intermolecolari sono trascurabili
3) il moto caotico delle particelle produce urti reciproci e con le pareti del recipiente perfettamente elastici.

Uno dei risultati più significativi della teoria cinetica dei gas è
l'aver dimostrato che la Pressione di un gas dipende dall'energia cinetica
media delle particelle che lo compongono![]() e dalla concentrazione del gas (numero di particelle
per unità di volume).
e dalla concentrazione del gas (numero di particelle
per unità di volume).
Per una mole di gas, composto da N molecole in un volume V, vale
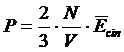
|
Relazione tra pressione , energia cinetica media e concentrazione delle particelle Consideriamo per semplicità una mole di un gas, ossia N molecole, contenute in un cubo di lato l, sufficientemente grande da poter trascurare gli urti reciproci tra particelle (il gas deve cioè essere sufficientemente rarefatto).Le particelle sono perciò libere di rimbalzare attraverso urti perfettamente elastici avanti e indietro tra due pareti opposte del cubo. Si supponga infine, per semplicità che 1/3 delle particelle si muova
parallelamente all'asse x, 1/3 parallelamente all'asse y ed 1/3
parallelamente all'asse z, con velocità media
Consideriamo ora una particella di massa m che rimbalza tra due pareti opposte con velocità Ad ogni rimbalzo la variazione della quantità di moto sarà dunque pari a Dalla dinamica sappiamo che l'impulso sulla parete (F.t) è pari alla variazione della quantità di moto Vogliamo ora calcolare la frequenza degli urti sulla parete, pari al numero di particelle che urta la parete nell'unità di tempo. Poiché tra un urto e l'altro la particella percorre uno spazio pari a
2l e lo spazio s percorso nel tempo
di un secondo è pari a s = numero urti al secondo = La quantità di moto che 1 molecola trasmette alla parete in un secondo è quindi pari alla frequenza degli urti per l'impulso di un singolo urto quantità di moto per particella al secondo = Poiché il numero di particelle che urtano una parete è N/3, la quantità di moto totale per secondo è Quantità
di moto totale per secondo = Ricordando che essa è pari all'impulso Ft e che in questo caso t è pari ad un secondo, la forza F che le particelle esercitano su di una parete è pari a poiché la pressione P è pari al rapporto tra forza F e superficie l2, otteniamo con l3 pari al volume V del recipiente La relazione permette di affermare che la Pressione è direttamente proporzionale al numero di particelle per unità di volume (N/l3) (concentrazione del gas) e all'energia cinetica media delle particelle. Si è ottenuta una relazione tra variabili macroscopiche (Pressione) e variabili microscopiche (concentrazione delle particelle ed energia cinetica media). |
La relazione può essere scritta anche
![]()
Analoga all'equazione di stato dei gas per 1 mole
PV = RT
Eguagliando i due secondi membri si ottiene

dove k è una nuova costante, detta costante di Boltzmann, pari al rapporto tra la costante dei gas R ed il numero di Avogadro N.
k = 1,3806 10-23 J/K (nel sistema SI)
k = 1,3806 10-16 erg/K (nel sistema cgs)
La relazione mette in evidenza il rapporto esistente tra un'altra
variabile macroscopica, la Temperatura, ed una variabile microscopica,
l'energia cinetica media delle particelle (![]() ).
).
La teoria cinetica dei gas dimostra per la prima volta che la temperatura di un corpo non è altro che l'espressione del moto disordinato delle sue particelle. Più precisamente possiamo affermare che la temperatura è una misura dell'energia cinetica media delle molecole che formano il gas
Attraverso la relazione precedente è ovviamente possibile calcolare la velocità quadratica media con cui si muovono delle molecole di massa nota, all'interno di un gas di temperatura T
![]() da
cui
da
cui 
La velocità quadratica media vrms (rms = root mean square) corrisponde alla radice quadrata della
media dei quadrati delle velocità delle particelle (in statistica è nota come
media quadratica) ed è leggermente diversa dalla velocità media ![]() .
.
Tenendo presente che k = R/N e che la massa di una molecola si può calcolare facendo il rapporto tra il suo peso molare ed il numero di Avogadro (m = Pm/N), sostituendo opportunamente la relazione diventa
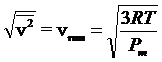
in cui utilizziamo i valori dei pesi molari, più comodi rispetto ai valori delle masse atomiche assolute (m) espresse in grammi.
L'equazione dimostra che ad una certa temperatura tutti i gas presentano la stessa energia cinetica media, ma velocità quadratica media diversa in funzione della loro massa.
Calcoliamo ad esempio la velocità quadratica media dell'Ossigeno molecolare O2 (Pm = 32 g/mol) a 20°C. Per ottenere il risultato in m/s è necessario usare tutte unità di misura del sistema internazionale. Dunque R = 8.31 Pa m3 K-1, mentre il peso molare andrà espresso in Kg/mol e dunque per l'Ossigeno sarà 32 10-3 kg/mol
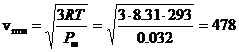 m/s
m/s
La velocità quadratica media può essere infine calcolata in funzione della pressione e della densità ρ (massa volumica) del gas.
Moltiplichiamo numeratore e denominatore sotto radice per il numero di moli n e per il volume V del recipiente, ottenendo
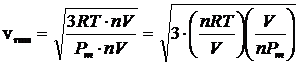
Si noti che la quantità (n·Pm)/V è il rapporto tra il peso di n moli ed il volume in cui sono contenute e rappresenta pertanto la densità ρ del gas (o massa volumica) espressa in kg/m3 (o, il che è lo stesso, in g/dm3 o g/L). La relazione diventa quindi
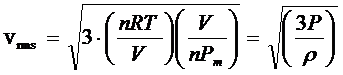
Calcoliamo ad esempio la velocità quadratica media di 3 moli di Ossigeno molecolare O2 (Pm = 32 g/mol) a 20°C contenute in un recipiente di 5L.
Anche in questo caso per ottenere il risultato in m/s è necessario usare tutte unità di misura del sistema internazionale. La pressione dell'ossigeno in pascal sarà
![]() Pa
Pa
3 moli di Ossigeno pesano 3 x 32 = 96 g = 0.096 kg e quindi la densità del gas è 0.096/0.005 = 19,2 kg/m3.
Sostituendo opportunamente si avrà in definitiva
 m/s
m/s
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Biologia |  |
| Lezioni Ingegneria tecnico |  |