 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2896 | Gradito: |
Leggi anche appunti:Parallassi annue e Parallassi di gruppoParallassi annue e Parallassi di gruppo Parallassi annue Eseguendo due osservazioni La recessione delle galassie: Red-shift e legge di HubbleLa cosmologia studia la struttura, l'origine e l'evoluzione dell'universo. Il Le leggi che regolano il sistema solareLe leggi che regolano il sistema solare Nonostante la complessità del Sistema |
 |
 |
Le leggi che regolano il sistema solare
Nonostante la complessità del Sistema solare, il moto che i pianeti compiono intorno al Sole può essere descritto da tre regole fondamentali assai semplici, chiamate leggi di Keplero, dal nome dell'astronomo e matematico che le scoprì nel XVII secolo:
La prima legge riguarda la forma
dell'orbita: i pianeti, compresa
La seconda legge riguarda la velocità con la quale i pianeti si muovono sulla loro orbita: ogni pianeta si muove sulla sua orbita in modo tale che la linea (raggio vettore) che lo congiunge al Sole, spazza aree uguali in tempi uguali. La terza legge mette in relazione la distanza di un pianeta dal Sole con il tempo necessario a percorrere l'intera orbita: il rapporto tra il quadrato dei tempi di rivoluzione dei pianeti e il cubo della loro distanza media dal sole è costante.
Le leggi di Keplero, essendo leggi empiriche, si limitano a descrivere il moto dei pianeti senza chiarirne le cause. Esse stabiliscono, introducendo elementi totalmente nuovi nelle concezioni dell'astronomia, che le orbite dei pianeti non sono circolari e che la velocità del loro moto non è costante.
La soluzione alla domanda rimasta fino ad allora insoluta, del perché i pianeti si muovano su un'orbita ellittica, fu trovata da Newton alla fine del XVII secolo. Egli riuscì a dimostrare che il moto dei pianeti e le scoperte di Keplero trovano spiegazione ammettendo che fra due corpi agisca una forza di attrazione F, che è direttamente proporzionale al prodotto delle masse m e m' e inversamente proporzionale al quadrato della loro distanza r. E' questa l'importantissima legge di gravitazione universale, espressa dalla formula:
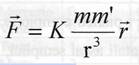
dove K è la costante di gravitazione universale e vale 6,67 x 10-11 Nm2 Kg-2 .
Un'altra legge che si dimostra fondamentale nella definizione matematica delle leggi di Keplero è la seconda legge della dinamica di Newton:
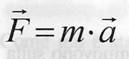
dove a è l'accelerazione del corpo di massa m soggetto alla forza F.
In particolare: poiché la forma delle orbite di un corpo intorno ad un altro risulta essere, a seconda della posizione e della velocità iniziali, una conica, cioè un'ellisse o una parabola o un ramo di iperbole, i due corpi in movimento reciproco descrivono tale orbita intorno al baricentro comune. Se tuttavia uno dei due corpi è più massiccio dell'altro, il baricentro coincide con la sua posizione e si può parlare di moto di un corpo intorno all'altro. La terza legge di Keplero viene precisata da Newton nella forma:
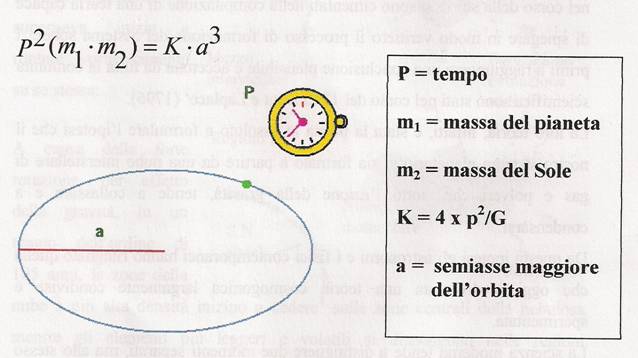
Nel Sistema solare la somma delle due masse, in prima approssimazione, si considera praticamente costante e pari alla sola massa solare, data la relativa piccola massa dei pianeti. Nel caso di sistemi binari di stelle, nei quali le masse stellari possono essere dello stesso ordine di grandezza, la terza legge di Keplero va utilizzata nella forma generalizzata di Newton.
Illustrate, dunque, queste note preliminari all'analisi delle circostanze di formazione del nostro sistema planetario è ora possibile analizzare dettagliatamente il modo in cui esso si è effettivamente formato e di come sia giunto alla sua situazione attuale.
 |
| Appunti su: |
|
| Appunti Archeologia |  |
| Tesine Geografia |  |
| Lezioni Ecologia ambiente |  |