 |
|
| Appunti tecniche |
|
 |
|
| Appunti tecniche |
|
| Visite: 1187 | Gradito: |
Leggi anche appunti:RELAZIONE D'ELETTRONICA - Rilievo della risposta di un filtro passa basso e passa altoRELAZIONE D'ELETTRONICA Rilievo della risposta di un filtro passa basso Controllo di CorrenteControllo di Corrente Il controllo di Corrente è stato inserito in modo Amplificatore antilogaritmicoAmplificatore antilogaritmico Scambiando l'elemento di ingresso con quello |
 |
 |
Ritardi introdotti dalle interconnessioni
Nel realizzare un circuito integrato bisogna effettuare delle interconnessioni che introducono una
serie di fenomeni non ideali (ritardi, ecc ). I materiali che possono essere utilizzati per fare un collegamento tra due nodi, in un dato layout, sono:

metal (m1) metal (m2) polisilicio (poly)
diffusioni n, p (ndiff, pdiff)
Il materiale migliore è probabilmente una linea di
metallo; quanti più livelli di metallo si hanno a disposizione, tanto più semplicemente si effettuano
le interconnessioni. Noi supporremo di avere a disposizione due livelli di metallo, che chiameremo
metal e metal , che sono separati da uno strato
isolante di ossido; quindi, sono indipendenti fra di loro, a meno di capacità parassite che eventualmente li possono collegare. Oltre a questi due livelli di metallo, per realizzare delle
interconnessioni, possiamo utilizzare del polisilicio ed anche delle diffusioni n e/o p. Ad esempio (Fig.
1.15), supponiamo di avere due linee
in metal1 nodi A e B) che vogliamo collegare fra di loro e tra le quali
passano trasversalmente un'altra linea di metal1 ed una linea di metal2.
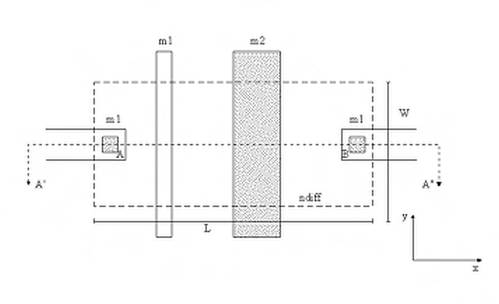
Fig. 1.15 -Esempio di interconnessione: utilizzo di una diffusione
Per collegare questi due terminali A e B bisogna realizzare due vie di collegamento ed utilizzare o del polisilicio oppure una diffusione n (o una diffusione p). La scelta del tipo di materiale sarà fatta in conformità a quale di questi è il migliore dal punto di vista dei parametri parassiti, cioè resistenza e capacità.
Per valutare la capacità di un rettangolo di regione diffusa ricordiamo che questa realizza con il substrato una giunzione.
dove Cj0 la capacità per unità di area e A=W.L è l'area del nostro rettangolo. Osserviamo che non possiamo pensare di utilizzare delle capacità variabili con la tensione, dato che vogliamo avere delle stime semplificate dei ritardi. Quindi, per effettuare una stima approssimativa dei ritardi, ci si pone nel caso (un pò irrealistico) peggiore possibile, ossia che la tensione inversa sia V=0. In tal caso si ha:
C C j A
Consideriamo la sezione A-A' del circuito di Figura 1.15. Come è possibile osservare (Fig. 1.16), oltre alla capacità per unità di area bisogna considerare anche il contributo dovuto alle regioni perimetrali. Allora è possibile approssimare questo aspetto scrivendo la capacità della nostra regione diffusa nel modo seguente:
C C b A C s P

Fig. 1.16 - Interconnessione mediante una diffusione:sezione del layout
dove Cb si misurerà in fF/ m e CS in fF/ m Tali parametri saranno forniti dal costruttore del circuito integrato in base alla tecnologia utilizzata e, quindi, non sono dei parametri di progetto su
cui è possibile agire, ma piuttosto delle costanti che sono assegnate una volta definita la tecnologia utilizzata. Questo discorso vale sia per le diffusioni n che per le diffusioni p.
Ridisegniamo la sezione del layout quando viene utilizzato il polisilicio per collegare i terminali A e
B, anziché la diffusione (Fig. 1.17).
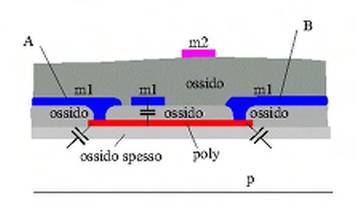
Fig. 1.17 - Interconnessione mediante polisilicio:sezione del layout
Osserviamo che lo strato di polisilicio è depositato su uno strato di ossido spesso (dato che non vogliamo realizzare un mosfet). Anche per il polisilicio possiamo esprimere la capacità come un
contributo per unità di area (C'b) moltiplicata per l'area A:
b
C C A
Osserviamo, però, che questa espressione è valida nel caso in cui si ha un condensatore le cui armature hanno un'estensione indefinita. Nel nostro caso, ci saranno anche dei fenomeni di bordo (sia nella direzione x che nella direzione y) che possono essere tenuti in conto, in maniera
approssimata, introducendo una capacità per unità di perimetro (C'S). ovvero si ha:
b
C C
A C P
S
Notiamo che i coefficienti C'b e C'S saranno completamente diversi da Cb e CS sia numericamente sia per il motivo fisico che è alla loro base. Nel caso del polisilicio si ha un condensatore che non è a facce piane e parallele, e quindi risente degli effetti di bordo; nel caso delle diffusioni c'è invece il
discorso delle diffusioni laterali e dei profili di drogaggio non
costanti.
Per il metall e il metal2 vale esattamente lo stesso discorso che è stato fatto per il polisilicio. Anche in questo caso si hanno dei condensatori in cui c'è dell'ossido come isolante, che sarà più spesso (essendo sottoposto a più passi tecno1ogici) e, quindi, le capacità saranno più piccole.
Osserviamo che oltre a queste capacità, fra linee e massa, esistono anche capacità fra linee e linee, che, in alcuni casi, possono essere significative. Ad esempio, ci sarà una capacità fra la linea di metall e quella di polisilicio (o di diffusione). Analogamente, ci sarà una capacità fra la linea di metal2 e il polisilicio, fra il metal2 ed il metal1, e così via. In definitiva, date le numerose linee presenti nel nostro circuito, dovremo definire una matrice di capacità molto complessa e stabilire anche dei criteri in base ai quali calcolare queste cross-capacitance (essendo impensabile valutarle tutte, dato che ciò renderebbe impraticabile qualsiasi tipo di simulazione). In pratica, per ogni linea, si definisce una sorta di "regione d'influenza" (valutata con algoritmi più o meno sofisticati), all'interno della quale si calcolano le capacità che eventualmente collegano tale linea con altre circostanti.
Nel nostro caso andremo semplicemente a valutare la capacità verso massa, disinteressandoci delle capacità fra linee distinte. Ciò potrebbe comportare dei problemi dato che, se queste ultime capacità sono abbastanza grandi, potrebbero dar luogo a fenomeni di malfunzionamento del nostro circuito che però si manifestano in maniera apparentemente casuale. Quindi, nel caso in cui si dispone di un tool di sviluppo sufficientemente accurato sarebbe opportuno tener conto di questo aspetto.
Per la valutazione delle resistenze parassite, consideriamo una linea di dimensioni l x w x t Fig.
1.18) attraversata da una certa corrente.
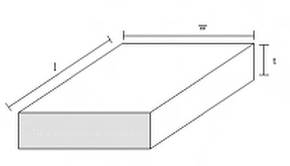
Fig. 1.18 - Valutazione delle resistenze parassite
Ad esempio, considerando una tecnologia a L=0.6 µm (ovvero =0.3 µm), i valori di resistenza e capacità sono i seguenti:
|
|
Cb [fF/ m |
CS [fF/ m] |
|
|
ndiff |
0.87 |
0.23 |
75 |
|
pdiff |
0.67 |
0.93 |
80 |
|
poly |
0.078 |
0.015 |
25 |
|
metal1 |
0.033 |
0.043 |
0.013 |
|
metal2 |
0.022 |
0.069 |
0.06 |
|
C'OX |
2.97 |
- |
- |
|
via m2 m1 |
- |
- |
3 |
|
via m1/poly |
- |
- |
25 |
Tab. 1.1 - Valori di resistenza e capacità per una tecnologia a L=0.6 m
Osservando la Tabella 1.1, è facile comprendere che gli elementi più sfavoriti per quel che riguarda la capacità sono le diffusioni n e p; il valore di queste capacità è circa un ordine di grandezza maggiore rispetto a quello del polisilicio. Ciò è dovuto al fatto che nel caso delle diffusioni l'equivalente del dielettrico è la sottile regione di svuotamento relativa alla giunzione, mentre nel caso del polisilicio è l'ossido spesso, che sicuramente ha uno spessore maggiore. Questo fatto ci spinge ad evitare (laddove possibile) l'utilizzo di diffusioni n e p per realizzare un collegamento. Notiamo ancora che la capacità per unità di area del metal1 è meno della metà di quella del polisilicio, e ancora più piccola è quella del metal2. Ciò dipende al fatto che ci sono strati di ossido via via più spessi che separano gli stati di metallo dal substrato. Dunque, i due layers metal1 e metal2 sono da preferire al polisilicio; d'altra parte la capacità per unità di perimetro tende ad essere maggiore per il metal1 e metal2 rispetto al polisilicio (dato che nei primi gli effetti di bordo sono più evidenti rispetto al polisilicio, che è più vicino al substrato). In ogni caso, in ordine di priorità, si considera prima il metallo e poi, eventualmente, il polisilicio. D'altro canto, ci sono una serie di vantaggi nel fare le interconnessioni in polisilicio, dato che esso va direttamente sulla gate di un mosfet (non è necessario fare dei contatti) e si può fare più sottile del metal (ci sono delle regole di progetto meno stringenti), e ciò fa si che molto spesso le interconnessioni vengano comunque realizzate in polisilicio anziché in metal.
Consideriamo l'esempio di layout di Figura 1.19 per avere un'idea dell'ordine di grandezza delle capacità in gioco.
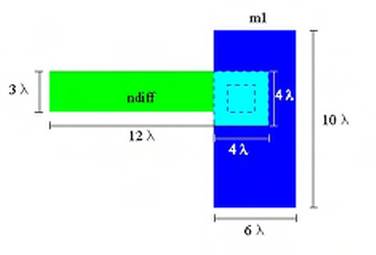
Fig. 1.19 - Esempio di layout: valutazione dell'ordine di grandezza delle capacità
Abbiamo una regione diffusa di tipo n larga e lunga 12 , una regione di contatto x λ e regione di metal1 di 6 x I valori di capacità (calcolati facendo riferimento alla Tabella 1.1) sono quelli riportati di seguito.
|
|
CAREA [fF] |
CPERIMETRO [fF] |
|
ndiff |
4.07 |
2.76 |
|
metal1 |
0.18 |
0.41 |
|
CTOT |
7.42 |
|
Notiamo che, per quanto riguarda il metal1, si potrebbe porre il problema di come considerare la zona in cui il metal1 corre sopra la diffusione. In altre parole, dobbiamo calcolare l'area come il prodotto 6 x 10 oppure dobbiamo sottrarre l'elemento 4 x 4 ? E, nel perimetro, dobbiamo portare in conto o meno tale zona? Teoricamente, dovremo eliminare la zona relativa al contatto dal calcolo dell'area della linea di metall, dato che sotto di esso non c'è il substrato, ma la regione diffusa. Inoltre, la capacità fra questi due elementi è cortocircuitata essendoci la via di collegamento. Comunque, questi sono tutti aspetti del secondo ordine; pertanto, in prima approssimazione, possiamo trascurare la presenza di queste sovrapposizioni e calcolare l'area come il prodotto W.L.
La capacità che abbiamo ottenuto (di circa 7fF) risulta essere legata quasi essenzialmente alla diffusione n (il metal1 contribuisce in maniera poco sensibile). Notiamo, inoltre, che per il metal1 è più importante la capacità perimetrale che non quella per unità di area. Tale valore va confrontato con la capacità di gate di un mosfet ad area minima, il cui valore è dato da:
Cg0=C'OX Wmin Lmin 5 (2 1.6 fF
Quindi la capacità delle interconnessioni è pari alla capacità di gate di un mosfet tutt'altro che ad area minima; quindi, la capacità CTOT è una capacità abbastanza significativa, ciò perché è stata utilizzata una regione diffusa di dimensioni abbastanza rilevanti.
Analogamente, calcoliamo la resistenza di una possibile interconnessione per avere un'idea dell'ordine di grandezza. A tale scopo consideriamo un'interconnessione in polisilicio del tipo mostrato in Figura 1.20
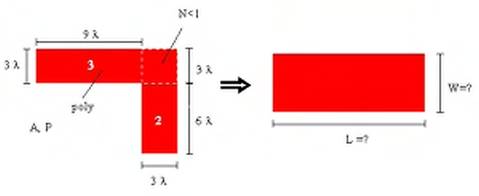
Fig. 1.20 - Esempio di interconnessione: valutazione della resistenza
Come osserviamo dalla Tabella 1. , le più grandi sono quelle relative alle regioni diffuse, con quella relativa alla diffusione p un poco più grande di quella della regione n, forse meno di quanto
ci aspettavamo, essendo la mobilità delle lacune minore di quella degli elettroni. Nonostante ciò, il rapporto delle due ρ è prossimo ad uno, il che vuol dire che la regione p è probabilmente più drogata della regione n (il che compensa la differenza di mobilità). La ρ del polisilicio è abbastanza più piccola delle regioni diffuse, ma non trascurabile. Invece il metal1 e il metal2 hanno delle resistenze di strato molto più basse; in particolare, il metal2 avrà uno spessore maggiore rispetto a quello del metal1, visto che la p è circa la metà di quella del metal1. Anche per quanto riguarda la resistenza delle interconnessioni, in ordine di priorità, è preferibile utilizzare il metal, poi il polisilicio ed, infine (proprio come ultima risorsa), le diffusioni.
Ritornando al nostro esempio, per valutare la resistenza bisogna calcolare il numero di quadrati in cui è possibile suddividere l'interconnessione. Questo calcolo non è così ovvio visto che la struttura dell'interconnessione non rettilinea. In ogni caso, c'è un tratto orizzontale che presenta 3 quadrati ed un tratto verticale che ne presenta 2, e resta da stabilire come valutare il quadrato in corrispondenza dell'angolo. In questo caso bisognerebbe risolvere un problema tutt'altro che banale: bisognerebbe imporre le condizioni al contorno, risolvere l'equazione di Laplace, vedere come vanno le linee di corrente e calcolare la resistenza. Ovviamente non possiamo operare in questo modo; è invece ragionevole considerare l'elemento d'angolo con un peso minore di 1 perché il cammino medio della corrente è minore di quello che si ha per un elemento rettilineo. Quindi, in definitiva, per il nostro numero di quadrati possiamo dire che 5<N<6.
Nel caso la struttura sia ancora più complessa, è possibile utilizzare degli algoritmi semplificati per avere una stima di N. L'algoritmo più semplice si basa sulla possibilità di sfruttare i parametri necessari a calcolare le capacità, quali sono l'area ed il perimetro. Dato il nostro elemento di interconnessione, consideriamo una sorta di rettangolo equivalente, di dimensioni L x W, che ha la stessa area e lo stesso perimetro della nostra interconnessione, ovvero:
W L A W L :
W L P
dove, in questo caso, la Isat è la corrente di saturazione di un NMOS con W/L 3/2. Da questo confronto è possibile stabilire se la resistenza dell'interconnessione è più o meno significativa.
Sappiamo che i valori di R0 sono dell'ordine del K ; quindi, nel nostro esempio la resistenza dell'interconnessione di 150 è in pratica trascurabile (visto che è un ordine di grandezza più
piccola). Osserviamo però che se il mosfet che pilota questa linea non è ad area minima ma ha un'area più grande, avrà una resistenza più bassa, e quindi la resistenza della linea di polisilicio potrebbe non essere più trascurabile.
Quindi, ancora una volta, nulla si può dire a priori: bisogna vedere dove è piazzato l'elemento di interconnessione, ovvero da quali mosfet è pilotato e, dal confronto con la resistenza equivalente di quest'ultimo, possiamo decidere di trascurare o meno la sua resistenza. Tipicamente, il confronto viene fatto con la resistenza equivalente dell'NMOS utilizzato come pull-down o del PMOS utilizzato come pull-up.
 |
| Appunti su: |
|
| Appunti Ingegneria tecnico |  |
| Tesine Gestione |  |
| Lezioni costruzione |  |