 |
|
| Appunti tecniche |
|
 |
|
| Appunti tecniche |
|
| Visite: 1632 | Gradito: |
Leggi anche appunti:RifasamentoRIFASAMENTO Le reti per la distribuzione per l'energia elettrica sono destinate Ritardi introdotti dalle interconnessioniRitardi introdotti dalle interconnessioni Nel realizzare un circuito integrato ComparatoreComparatore Il comparatore è simile al rilevatore di ero a parte il fatto |
 |
 |
Effetti dei ritardi introdotti dalle interconnessioni sulle prestazioni del circuito
Analizziamo ora, in maniera molto semplificata, in che modo la presenza delle capacità parassite introdotte dalle interconnessioni può influire sulle prestazioni (sui tempi di propagazione) del nostro circuito.
L'influenza di questi parametri parassiti dipende molto dal dimensionamento dei dispositivi attivi che fanno parte del nostro circuito integrato. Per chiarire meglio questo aspetto, consideriamo un semplice circuito di prova costituito da due invertitori in cascata (Fig. 1.21)
Fig. 1.21
- Esempio di interconnessione: valutazione
della resistenza

Come sappiamo i dispositivi di questo circuito sono dimensionati in modo tale che tutti abbiano la stessa L, pari alla dimensione minima che è possibile realizzare (per una data tecnologia ; il nostro grado di libertà è costituito dalle W dei dispositivi.
Supponiamo, per i dispositivi a canale n di scegliere una certa W, che indichiamo con Wn. Inoltre, per rendere simmetrico il funzionamento del nostro invertitore, la W del PMOS dovrà essere pari a Wn per un fattore che tiene conto della differente mobilità delle lacune rispetto agli elettroni. Questo fattore, µn/µp è un numero il cui valore è compreso fra 2 e 2.5 (secondo la particolare tecnologia realizzativa considerata). Supponendo, ad esempio (e per comodità di calcolo), che sia pari a 2, si ha Wp Wn
In definitiva, si ha che il nostro circuito è dimensionato a meno di un grado di libertà, che è il fattore Wn. Tale grado di libertà che abbiamo per l'invertitore nel nostro esempio, in realtà, lo possiamo avere per una qualsiasi porta logica CMOS. Ci si chiede, allora, come conviene scegliere questo grado di libertà: per rispondere a tale domanda analizziamo il tempo di propagazione del nostro circuito. Preventivamente dobbiamo valutare le capacità di carico, dovute alla capacità di gate dello stadio a valle (Cg e alle interconnessioni (Ci
Per valutare come bisogna scegliere Wn per minimizzare i ritardi basta analizzare l'andamento della costante di tempo in funzione di Wn (Fig. 1.22).
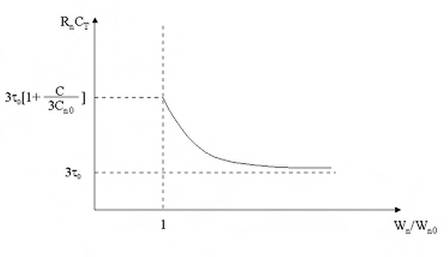
Fig. 1.22 - Andamento di Rn CT in funzione di Wn
Come è possibile osservare, al tendere di Wn Wn all infinito, la costante di tempo tende a in corrispondenza del valore minimo di Wn (ovvero Wn ), si ha un ritardo pari a 3 0 (l+Ci/3Cn Si
deduce allora che il dimensionamento del nostro circuito deve essere fatto avendo almeno un'idea di quella che sarà la capacità dell'interconnessione che bisogna pilotare. Se tale capacità è molto piccola, possiamo anche pensare di fare i dispositivi all'incirca ad area minima, dato che il ritardo 3 0 (l+Ci/3Cn0) sarà poco più grande di 3 0. Viceversa, se Ci è molto più grande di 3Cn0 si rischia, realizzando il circuito ad area minima, di avere un ritardo molto maggiore del valore teorico 3 0 che si può ottenere. Ovviamente, dato che la diminuzione del ritardo da un certo punto in poi diventa poco significativa, non conviene aumentare a dismisura Wn dato che, dopo un certo valore, si otterrebbero dei marginali miglioramenti del tempo di propagazione, a fronte di un aumento dell'area sempre maggiore. Quanto detto ci fa capire che, in pratica, non si utilizzano quasi mai dispositivi ad area minima, altrimenti il ritardo potrebbe essere sensibilmente influenzato da un'interconnessione, anche di dimensioni ridotte.
In tutto questo discorso non abbiamo tenuto in conto le capacità delle regioni diffuse dei nostri dispositivi (dei drain dell'NMOS e del PMOS). Bisogna stabilire se anch'esse sono proporzionali a Wn in tal caso per esse è possibile fare un discorso analogo a quanto fatto per Cg Inoltre ciò sarà uno stimolo a non fare dispositivi troppo grandi, dato all'aumentare di Wn, aumenta la capacità (Cn0+Cd ). Se invece, in base a come si riesce a realizzare il layout, le aree di drain risultano non proporzionali (o almeno non proporzionali con un fattore 1 di proporzionalità) a Wn potrebbe questo essere un ulteriore stimolo a non fare dispositivi ad area minima.
Quanto detto finora per l invertitore, vale per qualsiasi porta logica CMOS complessa. Anche in questo caso è possibile realizzare il nostro progetto avendo, alla fine, un grado di libertà (la dimensione di uno dei dispositivi). La scelta del valore da attribuire a tale grado di libertà dipende dalla capacità delle interconnessioni.
Un'interconnessione, oltre ad una capacità parassita, presenta anche una resistenza parassita. Consideriamo una situazione del tutto ideale in cui una linea d'interconnessione non è caricata in uscita (Fig. 1.23) ed è pilotata in ingresso da un generatore ideale di tensione. Pure in questo caso, del tutto ideale, ci sarà un ritardo fra il segnale d'ingresso applicato all'interconnessione ed il segnale d'uscita. Questa situazione ideale ci consente di valutare il cosiddetto ritardo intrinseco introdotto dall'interconessione

Fig. 1.23 - Caso ideale: linea di interconnessione non caricata in uscita
E' importante valutare questo ritardo intrinseco essenzialmente per stabilire se esso (come si spera) è sufficientemente piccolo in modo da poterlo trascurare. Tale ritardo intrinseco è dovuto al fatto che ogni pezzettino della linea d'interconessione, che è da considerarsi come una linea a parametri distribuiti, ha una resistenza ed una capacità; quindi, ognuno di questi pezzettini introduce un elemento di ritardo. Per studiare questo circuito, dividiamo la nostra linea in tanti pezzettini, ognuno dei quali è approssimato con una resistenza R ed una capacità C verso massa. Supponendo che tali pezzettini abbiano tutti le stesse dimensioni, associamo loro uno stesso valore di R e di C. Il sistema che ne risulta è di tipo passa-basso, quindi possiamo approssimare la risposta del nostro sistema mediante un sistema equivalente del primo ordine, utilizzando la tecnica delle costanti di tempo.
Dunque si ha che eq L , il che è evidente visto che sia RT che CT aumentano con L. Ciò che forse è meno evidente è che il eq cresce al diminuire di W. Questo è dovuto al fatto che, mentre la
resistenza è inversamente proporzionalmente a W, la capacità presenta il termine perimetrale che è all'incirca indipendente da W. Questo fattore aggiuntivo fa si che la costante di tempo equivalente cresce al decrescere di W. Per avere un'idea dell'ordine di grandezza di tale costante di tempo consideriamo una linea in polisilicio con L =300µm e W=0.6µm; in tal caso si ottiene un ritardo pari a 0.69 eq 0.l8ns (che è lo stesso ordine di grandezza del parametro 0 di un invertitore). In questo esempio, però, abbiamo considerato una linea di polisilicio lunga 300µm; quindi, nei casi pratici (a meno di casi particolarmente strani) il ritardo intrinseco introdotto da un'interconnessione può essere tranquillamente trascurato. Infatti, se, invece del polisilicio, avessimo usato una linea di metallo tale ritardo si sarebbe ridotto di più di un ordine di grandezza. Ricordiamo, però, che tale ritardo cresce comunque con il quadrato della lunghezza della linea.
In definitiva, i modelli che possiamo utilizzare per portare in conto il ritardo introdotto dalle interconnessioni sono, sostanzialmente, quelli riportati in Figura 1.24.
Considerando due invertitori in cascata, al livello di approssimazione (1) consideriamo la sola capacità introdotta dall'interconnessione Ci. Al livello di approssimazione (2) possiamo tenere in conto anche della resistenza serie R dell'interconnessione. Al livello (3) sono considerati anche gli aspetti distribuiti, ovvero l'interconnessione è considerata come una linea di trasmissione. Ovviamente c'è anche il livello (0) in cui sono trascurati del tutto gli effetti parassiti delle interconnessioni.
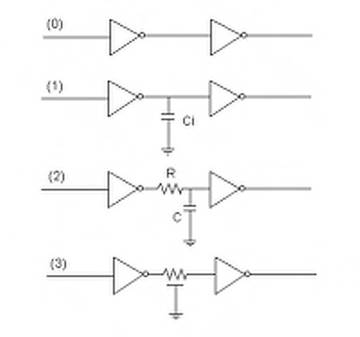
Fig. 1.24 - Modelli per portare in conto il ritardo delle interconnessioni
Dall'analisi fatta in precedenza deduciamo di poter tranquillamente trascurare il modello che considera gli elementi distribuiti, poiché l effetto del ritardo intrinseco è generalmente molto piccolo. Inoltre, l'effetto della resistenza serie della linea di interconnessione può essere trascurato o meno in base alle resistenze equivalenti dei dispositivi che costituiscono la nostra porta logica. Se, come tipicamente accade, queste resistenze sono abbastanza più grandi di R, allora l'effetto di tale resistenza può essere trascurato nei nostri calcoli. Quindi per la maggior parte dei casi faremo riferimento al modello (1), in altre parole approssimando l'interconnessione con una semplice capacità. Viceversa, non portare in conto la capacità dell'interconnessione può comportare degli errori molto grandi, quali ad esempio quello di dimensionare tutti i dispositivi ad area minima, che abbiamo visto non essere una buona scelta.
Solo per alcune linee particolarmente critiche può essere utile valutare l effetto della resistenza serie dell'interconnessione, considerando quest'ultima sempre come un elemento a parametri concentrati. Il ritardo dovuto alle resistenze serie delle interconnessioni è particolarmente importante per una sola interconnessione del nostro circuito, quella relativa alla linea di clock. Infatti, se abbiamo un sistema sequenziale, si avranno dei registri di memoria che catturano il dato al loro ingresso in corrispondenza dei fronti del segnale di clock. Il funzionamento del nostro circuito si basa sull'ipotesi che questi fronti del segnale di clock arrivino, nello stesso istante, a tutti registri del nostro circuito. Nel momento in cui ciò non accade, un registro può memorizzare un dato quando questo ancora non è valido, o quando questo sta ancora cambiando. Questo, ovviamente, non significa peggiorare le prestazioni del nostro sistema ma, piuttosto, che il sistema non funziona più. E' importante stabilire qual è il ritardo massimo che possiamo aspettarci sulla linea di clock e adottare le opportune contromisure. Abbiamo un ritardo sulla linea di clock proprio perché la linea di interconnessione non è ideale. Bisogna, allora, saper stimare il ritardo clock su questa linea di clock e, una volta stimato tale ritardo, garantire la funzionalità del nostro circuito.

Fig. 1.25 - Stima del ritardo sulla linea del clock
Consideriamo una situazione limite mostrata in Figura 1.25. Abbiamo un circuito che genera il segnale di clock (clock driver), un primo registro che si trova nelle immediate vicinanze del clock driver e una lunga linea di interconnessione (schematizzata con la sua resistenza e la sua capacità) che pilota un banco di registri posizionati ad una certa distanza dal primo registro. Dobbiamo valutare allora il ritardo clock fra l'istante di tempo in cui il fronte di clock arriva al registro in prossimità del clock driver e l'istante di tempo in cui il fronte arriva dall'altra parte della linea. Tale ritardo é dato da:
clock Rclock C
La capacità totale C è la somma di due contributi: un contributo dovuto alle interconnessioni (Ci) ed uno legato alle capacità di gate dei vari flip-flop comandati dalla linea di clock (Cg). Ad esempio, supponiamo di avere un registro da 16 bit (16 flip-flop). Ogni flip-flop ha, al suo interno, i seguenti elementi di layout: un rettangolo equivalente di metal1 di 30µm x 12µm, un rettangolo equivalente di poly di 20µm x 0.8µm, 8 NMOS con W/L=12 e 8 PMOS con W/L=30 (ipotizzando =0.3µm). La capacità totale C risulta essere pari a circa l80fF per ogni flip-flop ed è dovuta quasi essenzialmente ai mosfet (la capacità delle interconnessioni risulta essere, infatti, dell'ordine di 5÷6fF). La capacità associata all'intero registro è allora pari a Cregistro=l6xl80fF 2.9pF. La capacità associata all'interconnessione sarà certamente più piccola di tale valore, possiamo quindi trascurarla; viceversa, non possiamo trascurarne la resistenza. Se supponiamo che questa linea di interconnessione sia realizzata in polisilicio, lunga 4 m e larga 0. m si ha 0.69 Rclock Cregistro
ns, che risulta essere un ritardo abbastanza consistente (il che può portare ad errori di sincronizzazione del nostro circuito). Se utilizziamo il metallo per tale interconnessione, a parità di dimensioni, otteniamo un ritardo di circa 30 ps (valore certamente più accettabile rispetto a quello relativo al polisilicio) Osserviamo, però, che se consideriamo un banco di 32 registri da 16 bit otteniamo, anche se utilizziamo una linea in metal, un ritardo di circa 900 ps. In questo caso il ritardo risulta essere non più accettabile e ciò che ci resta da fare allargare la linea, in modo da ridurne la resistenza Rclock.
Quanto detto risulta essere uno dei problemi più significativi, in particolare per i microprocessori
più avanzati, in cui le capacità che si hanno sul clock sono dell'ordine di decine di nF; quindi è fondamentale avere un'idea del ritardo sulla linea di clock. In questi casi un parametro importante può essere la resistenza del contatto; pertanto si realizzano più contatti in parallelo per ridurre la resistenza serie ad essi associata.
In ogni caso questo ritardo non si riesce a portarlo zero, ma sarà ridotto ad un certo valore minimo. In queste condizioni bisogna garantire che il circuito funzioni correttamente, e ciò può sempre essere realizzato progettando opportunamente la temporizzazione del nostro sistema.
Linee di alimentazione
Per le linee di alimentazione possiamo individuare due tipi di problemi, uno legato al fenomeno dì migrazione metallica ed un altro legato alla presenza dei cosiddetti "rimbalzi" delle linee.
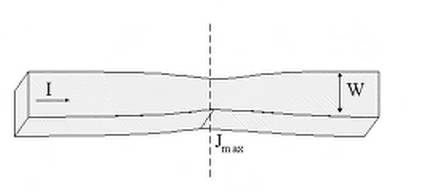
Fig. 1.26 - Effetti della migrazione metallica
Consideriamo una linea di metal nella quale passa una certa corrente I (Fig. 1.26) e supponiamo che una parte di questa linea, a causa di un imperfezione costruttiva, sia più sottile rispetto al resto della linea. La densità di corrente J=I/A (con A=sezione della linea) avrà un massimo proprio in corrispondenza di tale punto. I grani metallici che compongono la linea possono migrare seguendo il flusso della corrente, e tale migrazione è ovviamente tanto più forte laddove maggiore è la J. Nel nostro caso, tale fenomeno sarà particolarmente evidente nel punto in cui la linea è più stretta. Si innesca allora un fenomeno rigenerativo dato che, nel momento in cui i grani metallici migrano, la sezione della linea si riduce e ciò comporta un ulteriore aumento di J. Ciò può portare alla rottura della linea.
Il problema è che questo fenomeno può avvenire con scale dei tempi che possono essere molto lunghe, dando luogo a problemi di affidabilità del circuito. Per evitare che si abbia un fenomeno di questo tipo, è necessario limitare la corrente che passa in una linea, o meglio la densità di corrente deve essere sufficientemente bassa. Il costruttore del circuito integrato fornisce quindi un valore massimo di corrente assegnato in A/µm, ampere per µm di larghezza della linea, essendo la larghezza W 1'unico parametro su cui si può agire (dato che lo spessore dipende dalla tecnologia costruttiva). Questo valore di corrente massima, Imax è dell'ordine di 1mA/ m, che è da intendersi come valor medio di corrente. Essendo la corrente che attraversa la linea non perfettamente costante, ma anzi con picchi attorno ad un valore medio, il costruttore, oltre a fornire questo massimo valore di corrente media, fornisce anche i valori massimi tollerabili di corrente di picco.
Per valutare la corrente media, consideriamo il circuito di Figura 1.27 (per semplicità consideriamo un invertitore che pilota una capacità, ma si potrebbe adattare ad una qualsiasi porta logica, dato che la potenza si esprime sempre allo stesso modo).

Fig. 1.27 - Circuito per il calcolo di Imax
Bisogna perciò realizzare la linea di alimentazione sufficientemente larga, tale che la densità di corrente sia sufficientemente bassa ed il fenomeno di migrazione metallica non abbia a verificarsi. Anche il problema dei "rimbalzi" sulle linee di alimentazione impone un vincolo su W. Consideriamo ancora un invertitore ma potrebbe essere una qualsiasi porta logica), in cui la linea di alimentazione non è proprio ideale ma ha una sua resistenza serie R (Figura 1.28). Supponendo che l'ingresso abbia una transizione 1 0 si ha che il PMOS entra in conduzione, l'NMOS s'interdice e si ha una corrente che va a caricare la capacità C. Si ha allora una caduta di tensione sulla resistenza R pari a R ic. Questa caduta di tensione prende il nome di "rimbalzo" sull'alimentazione essendo una conseguenza della commutazione dell'uscita. La corrente ic non è la stessa del caso precedente, dato che qui si tratta di una corrente istantanea.

Fig. 1.28 - Circuito per la valutazione dei "rimbalzi"
La corrente istantanea può essere stimata valutando l'andamento della tensione di uscita vo (Fig. 1.29) e ricordando che ic=C dvo/dt
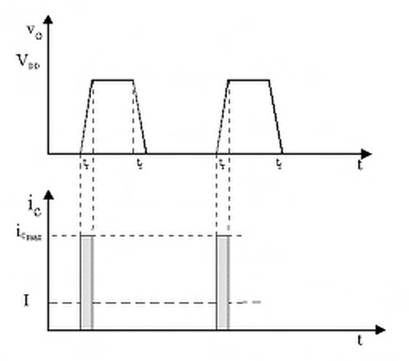
Fig. 1.29 - Andamento della tensione di uscita e della corrente ic
Il valore massimo di corrente sarà dato da:
i = C VDD
t
![]()
c max
r
Ciò vuoi dire che la corrente assorbita dall'alimentazione ha una serie di impulsi in corrispondenza dei fronti dell'uscita, il cui valore medio è pari ad I (di cui parlavamo a proposito della migrazione metallica, e che dipende dal periodo del segnale, ovvero dalla frequenza).
Tale rimbalzo della tensione d'uscita sulla linea di alimentazione è, ovviamente, fastidioso in quanto il potenziale corrispondente al nodo P, durante la commutazione, si abbassa di una quantità
proprio pari a VR. Se tale punto alimenta un'altra porta logica questa si troverà istantaneamente ad una tensione d'alimentazione più bassa di VDD e ciò può comportare tutta una serie di problemi (i margini di rumore cambiano, l'uscita di questa porta comincia a fluttuare invece di rimanere costante, ecc.). E' necessario allora limitare questo fenomeno di rimbalzo sulle linee di alimentazione; in altri termini, questo VR deve essere abbastanza più piccolo dei margini di rumore del nostro circuito (dell ordine di qualche centinaio di mV. essendo i margini di rumore dell'ordine di 1.5 2V, per una tensione di alimentazione di 5 V).
Sceglieremo dunque W come il valore massimo tra questo valore è quello che si ricava dal vincolo dovuto al fenomeno della migrazione metallica.
Ad esempio, consideriamo una frequenza f=50MHz, una capacità C=l00pF (la tipica capacità di una linea di clock), una tensione di alimentazione VDD=5V e un tempo di salita/discesa tr = tf 1ns. Per
valutare il primo vincolo, dovuto alla migrazione metallica, calcoliamo la potenza dissipata che vale PD= 125 mW, da cui il valore della corrente media, I=25 mA. Allora, se abbiamo una Imax di 1mA/µm si ha che W>25µm (anche se, per maggiore sicurezza, conviene fare la linea un poco più grande). Supponendo di aver progettato la linea in questo modo vediamo cosa si ha per quanto riguarda il problema dei rimbalzi. La icmax risulta essere pari a 0.5 A che per un circuito microelettronico è un valore molto grande, rispetto al valore medio di 25mA. Ciò, ovviamente, è dovuto al tempo di salita che è una piccola frazione del periodo. Il valore di W, a questo punto, sarà determinato dalla lunghezza della linea: per una lunghezza L=25 m (100 quadri con W=25 m) si avrebbe VR 0.5V, che sicuramente è un valore inaccettabile. Bisognerebbe, quindi, o aumentare W o cercare di ridurre L. Osserviamo che L=2 m può sembrare un valore molto grande, ma in realtà è un valore realistico, poiché bisogna tener presente che le linee di alimentazione devono arrivare a tutte le porte logiche del nostro chip. In definitiva, per ridurre il VR bisogna aumentare W oppure aumentare tr, in particolare per i terminali di uscita del chip che pilotano le capacità di carico, il cui valore può non essere noto a priori (e che può essere anche di centinaia di F). Per questo motivo, tutti i terminali di ingresso/uscita vengono progettati per minimizzare il ritardo di propagazione, ma portando in conto che il tempo di salita non deve essere troppo basso (altrimenti il picco di corrente che può passare diventa eccessivo, pregiudicando il funzionamento del circuito): in tal caso, si dice che c'è un limite sulla slew-rate della tensione d'uscita.
Layout editor: layout simbolici ed effettivi, stick-diagrams
Utilizzando un layout editor tipo MAGIC (distribuito dall'Università di Berkley) non vi è la necessità di dover disegnare la n-well, ossia la regione diffusa nel substrato per ospitare i PMOS; inoltre, nelle zone di contatto non sono evidenziate le regioni in cui sono effettivamente realizzate le vie di collegamento. Il motivo di ciò è che il layout-editor che comunemente utilizziamo è di tipo simbolico ed il layout che si ottiene rappresenta, in qualche modo, una sorta di livello di astrazione più alto rispetto al layout effettivo del circuito, altri non è che l'insieme delle maschere che servono per progettare il nostro circuito integrato. Con questo layout-editor, allora, non si disegnano le effettive maschere da utilizzare, ma qualcosa di più semplice da cui è possibile ottenere le maschere necessarie per la fabbricazione del nostro circuito. Il passaggio da layout simbolico a layout effettivo avviene, comunque, in maniera del tutto automatica, grazie a delle opportune routine: a partire dal layout simbolico, il layout effettivo è sicuramente corretto per costruzione.
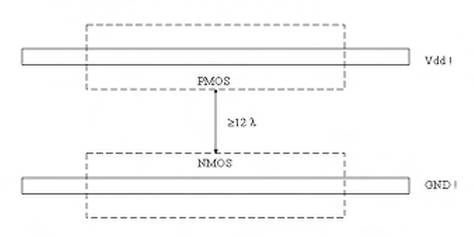
Fig. 1.30 - Struttura tipica di un layout
Fra le varie regole di progetto, la più rilevante è quella relativa alla distanza (spacing) fra le regioni n-diff e p-diff, che deve essere maggiore o uguale a 1 , un valore molto maggiore rispetto alle
altre regole di progetto. Le regioni diffuse di tipo n e di tipo p devono essere così distanti fra loro perché si deve consentire la realizzazione della n-well (che include le diffusioni di tipo p e i contatti relativi alla well). Quindi, questa è la regola più stringente ed è quella che vincola maggiormente il nostro progetto in termini di occupazione di area. Infatti, dovendo rispettare sia questa regola che il dover mettere quante più prese di substrato sia possibile vicino agli NMOS ed ai PMOS, il layout (qualunque esso sia) avrà sempre una struttura del tipo mostrato in Figura 1.30.
Come riportato in figura, si avranno due linee di alimentazione: una linea di alimentazione positiva chiamata, per convenzione, "Vdd !" ed una linea di massa, chiamata "GND!". Il punto esclamativo indica che si tratta di nodi globali, cioè riferimenti assoluti di alimentazione e massa.Lungo la linea Vdd! saranno piazzati i PMOS, mentre sulla linea GND! saranno piazzati gli NMOS, mantenendo una distanza di almeno 12 fra i dispositivi NMOS e PMOS. I PMOS sono piazzati vicino alla linea Vdd! (gli NMOS vicino alla linea GND!) perché così è più semplice realizzare le prese di substrato. Nel realizzare il layout del nostro circuito, invece che disegnare di volta in volta i vari rettangoli, conviene partire da un disegno semplificato, che prende il nome di stick-diagram (diagramma a stecchino). Nello stick-diagram si disegnano semplicemente le posizioni relative dei vari elementi, senza tener conto delle effettive dimensioni dei rettangoli. Ogni layer è rappresentato con una linea che avrà un colore o un tratteggio differente (Figura 1.31).
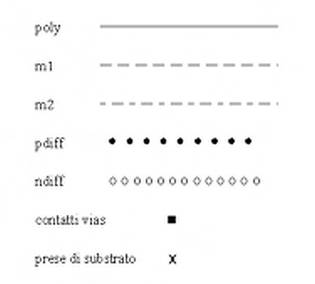
Fig. 1.31 - Rappresentazione dei layers in uno stick-diagram
Ad esempio, al polisilicio si fa corrispondere una linea continua, al metall una linea tratteggiata, ai metal2 una linea tratto e punto, alla diffusione n una sequenza di cerchi vuoti, alla diffusione p una sequenza di cerchi pieni, i contatti sono rappresentati mediante dei rettangoli pieni mentre le prese di substrato con delle 'x'. Ovviamente, per ognuno di questi layers, non specifichiamo né le dimensioni, né la distanza fra loro. Lo stick-diagram ci serve solo per capire come in seguito sarà organizzato il layout. Ciò è molto importante perché ci sono degli algoritmi che consentono, in molti casi, di ottenere in maniera automatica il layout, e quindi lo stick-diagram. Vediamo adesso cosa succede quando due linee si intersecano in uno stick-diagram; le varie combinazioni sono riassunte nella Tabella 1.2.
|
|
m2 |
m1 |
poly |
n-diff |
p-diff |
|
m2 |
corto circuito |
circuito aperto |
circuito aperto |
circuito aperto |
circuito aperto |
|
m1 |
circuito aperto |
corto circuito |
circuito aperto |
circuito aperto |
circuito aperto |
|
poly |
circuito aperto |
circuito aperto |
corto circuito |
NMOS |
PMOS |
|
n-diff |
circuito aperto |
circuito aperto |
NMOS |
corto circuito |
Illegale |
|
p-diff |
circuito aperto |
circuito aperto |
PMOS |
Illegale |
corto circuito |
Tab. 1.2 - Interpretazione delle possibili intersezioni tra layers in uno stick-diagram
Le intersezioni illegali sono ovvie in quanto i layer p-diff ed n-diff devono distare almeno 1

Fig. 1.32 - Stick-diagram di un invertitore
Ad esempio, lo stick-diagram di un invertitore sarà del tipo mostrato in Figura 1.32. Supponendo di dover passare una segnale k da sinistra a destra del circuito, la soluzione più immediata è quella di utilizzare una linea metal2. Supponiamo, però, di non poter utilizzare il metal2 (perché, ad esempio, ci sono altri due nodi da collegare, scavalcando anche il segnale k). Modifichiamo allora il nostro
1ayout in modo da renderlo, come suol dirsi, "trasparente al metal1". Una possibile soluzione è mostrata in Figura 1.33, in cui il collegamento verticale relativo all'uscita è realizzato in polisilicio, utilizzando altri due contatti orizzontali ed un altro contatto per riportare l'uscita da poly a metal1 (se necessario). Notiamo che non si può realizzare un contatto diretto fra diffusione e polisilicio poiché, essendo il processo autoallineato, il polisilicio è depositato prima delle diffusioni..
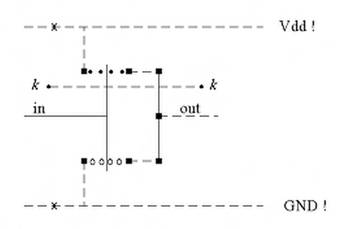
Fig. 1.33 - Stick-diagram di un invertitore "trasparente al metal1": prima soluzione
Gli svantaggi di quest'approccio sono dovuti al fatto che si è realizzata la linea verticale in uscita al polisilicio. La lunghezza di questa linea è dell'ordine di 12 , per una larghezza di almeno 2
Quindi la lunghezza di questa linea di poly è dell'ordine di 6 quadrati, ognuno dei quali presenta una resistenza di circa 3 ; in uscita, pertanto, si ottiene intorno ai 1 0 , che tipicamente è
inferiore alle resistenze equivalenti degli NMOS e dei PMOS. Quindi, l'effetto di questa resistenza, seppur presente, è abbastanza trascurabile. Ciò che, invece, non può sicuramente esser trascurata è la capacità della linea di polisilicio, che peggiora il nostro circuito in termini di velocità, potenza dissipata, e così via.
Un'altra possibile soluzione è riportata in Figura 1.34.
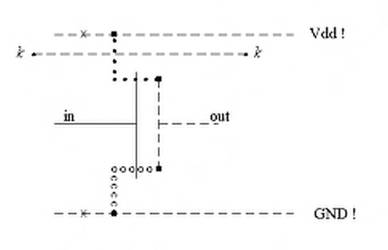
Fig. 1.34 - Stick-diagram di un invertitore "trasparente al metal1 : seconda soluzione
La soluzione qui adottata è cambiare la disposizione delle regioni diffuse, realizzandole ad angolo retto. In questo modo abbiamo guadagnato uno spazio (sopra il PMOS e sotto l'NMOS) attraverso cui è possibile far passare la linea di collegamento in metal1. Tale linea, ovviamente, non può essere in polisilicio altrimenti, in serie al PMOS, si crea un altro mosfet a canale p che pregiudica il funzionamento dell'invertitore. Rispetto all'invertitore originario, si sono aumentate le dimensioni delle regioni diffuse e, dunque, le resistenze e le capacità dei dispositivi. Per le resistenze vale un discorso analogo a quanto detto prima: il numero di quadrati aggiuntivi, per allungare le regioni diffuse, molto probabilmente non è così elevato da alterare apprezzabilmente la resistenza serie dei mosfet. Occorre allora stimare l'effetto delle sole capacità delle regioni diffuse (che sono abbastanza grandi).

Fig. 1.35 - Invertitore: circuito relativo allo stick-diagram di figura 1.34
Lo schema circuitale di Fig.1.35 illustra la collocazione delle capacità aggiuntive che, per come è stata progettata la linea in polisilicio che collega le gate dei mosfet, sono disposte tra i terminali di source e substrato dei due mosfet. Ma, poiché queste due regioni sono connesse all'alimentazione (PMOS) ed alla massa (NMOS), queste capacità sono cortocircuitate e, perciò, ininfluenti.
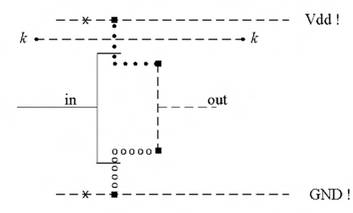
Fig. 1.36 -Influenza della capacità di diffusione
Viceversa, se modifichiamo lo stick-diagram come mostrato in Figura 1.36, le capacità sono collocate tra il drain ed il substrato dei mosfet, ossia in uscita all'invertitore. Ciò comporta un rallentamento del circuito ed un sensibile aumento della dissipazione di potenza.
Come ulteriore esempio, riportiamo in Figura 1.37 lo stick-diagram di una porta NAND con ingressi A e B. Si noti che i due NMOS in serie sono semplicemente dati dall'adiacenza delle due linee di polisilicio della gate. A meno che non vi siano motivi per accedere al nodo X, non c'è la necessità di usare una via, ed il collegamento tra il drain del NMOS sottostante X ed il source del NMOS sovrastante X è dato dalla continuità della regione ndiff.
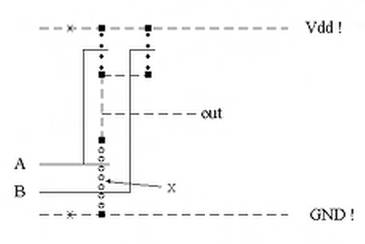
Fig. 1.37 - Stick-diagram di una porta NAND
 |
| Appunti su: |
|
| Appunti Ingegneria tecnico |  |
| Tesine costruzione |  |
| Lezioni Gestione |  |