 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2027 | Gradito: |
Leggi anche appunti:Schopenhauer, la liberazione nel piacere esteticoSchopenhauer, la liberazione nel piacere estetico Negli scritti di Arthur Integrale indefinitoINTEGRALE INDEFINITO Definizione (di funzione primitiva) Sia L'affascinante mondo dei frattaliL'AFFASCINANTE MONDO DEI FRATTALI LA |
 |
 |
Validazione Algoritmo
1 Implementazione software
Tra i vari problemi affrontati nell'implementare l'algoritmo nel simulatore ci sono stati difficoltà nell'integrare la funzione di minimizzazione nel simulatore preesistente causate da incompatibilità tra librerie. Il software usava librerie standard C++, quali la <math.h>, <iostream.h>, <fstream.h>, dovendo utilizzare delle funzioni ottimizzate che usavano la libreria <complex.h>, si sono creati conflitti tra istruzioni che avevano dichiarazioni contrastanti.
Inoltre, il simulatore su cui doveva essere implementata la funzione gestiva i numeri complessi dividendoli in parte Reale ed Immaginaria, quindi ogni vettore aveva dimensioni doppie del necessario per ospitare tutti gli elementi. La funzione per la decomposizione SVD della matrice usa invece la libreria <complex> che gestisce diversamente i numeri complessi.
Un matrice MxN da decomporre tramite SVD, è in realtà un vettore di dimensione MxN in cui gli elementi sono inseriti nel seguente modo:
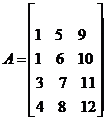
![]() A=[1,2,3,4,5,6,7,8,9,10,11,12]
A=[1,2,3,4,5,6,7,8,9,10,11,12]
Seguendo le fasi dell'implementazione dell'algoritmo LSQI, dobbiamo inizialmente creare la matrice C contenente i campioni dello spettro delle CCs. Ogni colonna della matrice corrisponde allo spettro di una CCs, alternando parte in fase e quadratura del segnale. Lo stesso per il vettore s che contiene i campioni dello spettro del segnale utile. Dobbiamo fare attenzione quando passiamo gli argomenti alla funzione che fa l'ottimizzazione:
sia la matrice che il vettore avranno dimensioni delle colonne pari alla metà di quelle di partenza, perché due elementi consecutivi su una colonna corrispondono ad un numero complesso.

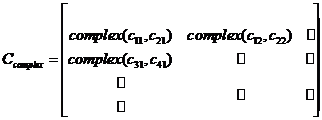
CCs1 CCs2 CCs3
![]() . In raltà
. In raltà ![]() sarà:
sarà: ![]() .
.
Dopo aver sistemato i vettori che devono essere elaborati dalla funzione zsvd (che fa la decomposizione SVD della matrice) è stato implementato il metodo di Newton per calcolare il vettore incognito dell'algoritmo LSQI.
Per verificare il giusto funzionamento dell'algoritmo abbiamo preso l'esempio numerico di [1] ed abbiamo fatto elaborare i dati dal nostro codice C++.
2 Verifica del funzionamento dell'algoritmo
Per avere una prima riprova della correttezza dell'algoritmo ci siamo messi in una situazione semplice computazionalmente.
E' stato inizialmente graficato uno spettro composto da 64 sottoportanti in totale, 60 di queste servono per la trasmissione dati, le rimanenti 4 sono le CCs.
Applichiamo l'algoritmo di minimizzazione provando a variare la potenza fornita alle CCs.
Illustriamo di seguito i grafici ottenuti nel caso:
Volendo graficare lo spettro centrato sullo zero, attiviamo le portanti [-30, 29] mentre le CCs risulteranno -32,-31, 30, 31, per un totale di 64 sottoportanti.
Il range di ottimizzazione comprende le code a sinistra della CCs= -32 e a destra della CCs=31. La risoluzione dei grafici non risulta buona, in quanto abbiamo preso due campioni per ogni lobo della sinc, quindi il campione sullo zero ed il campione sul massimo del lobo laterale come mostrato in Fig.1. Cosi facendo sono stati ridotti i massimi dei lobi laterali.

Fig.1
In Fig.2 mostriamo lo spettro del segnale dati.

Fig.2
Lo spettro delle CCs prima della pesatura è dato dalla somma delle sinc in Fig.3.
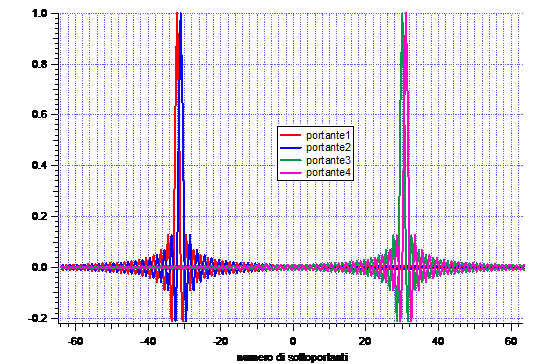
Fig.3
Il vettore delle incognite fornito dall'algoritmo di minimizzazione sarà composto da elementi Reali, questo perché i simboli sulle sottoportanti sono a parte Immaginaria nulla. I valori del vettore incognite in questo caso particolare sono i seguenti:
 .
.
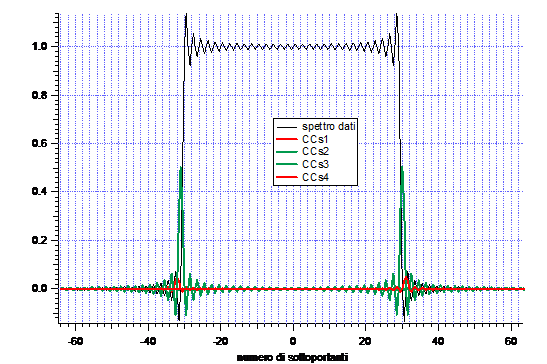
Fig.4
Risulta evidente come le code dello spettro di partenza vengano attenuate con l'introduzione delle CCs opportunamente pesate con l'algoritmo.
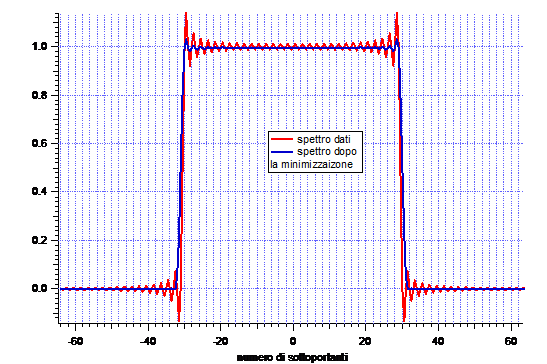
Fig.5
Il fattore A di cui si parla nel cap.III risulta essere A=0.99570166874728 < 1.
Aumentando la potenza spesa sulle CCs vediamo cosa otteniamo di diverso rispetto al caso precedente:
0.1% di potenza 
0.3% di potenza 
0.5% di potenza  che risulta essere lo
stesso vettore del caso di potenza pari al 5%.
che risulta essere lo
stesso vettore del caso di potenza pari al 5%.
Grafichiamo lo spettro al variare della potenza investita sulle CCs per verificare l'efficienza dell'algoritmo. Vediamo che aumentando la potenza da 0.1% allo 0.5% i lobi laterali vanno sempre più scomparendo.
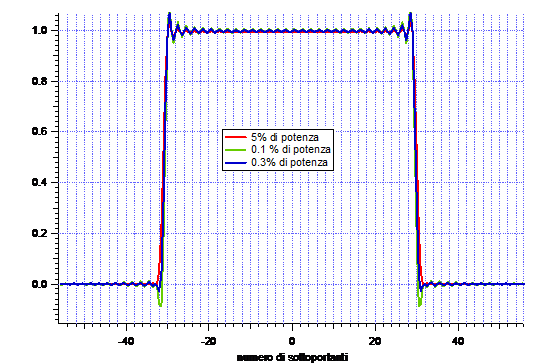
Fig.6
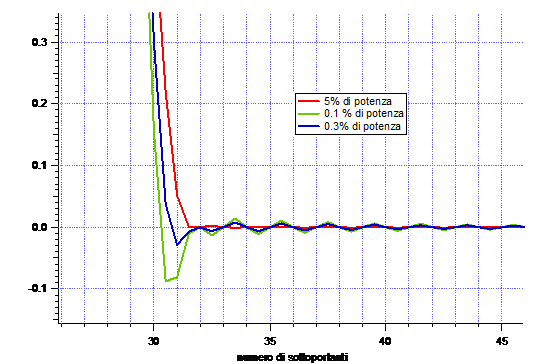
Fig.7
Nella Fig.7 viene riportato il particolare dei lobi laterali sulla destra dello spettro. Vediamo che aumentando la potenza dal 0.1% al 0.5% si ha un miglioramento, ma oltre lo 0.5% non ci sono cambiamenti, infatti il vettore delle incognite rimane invariato. Questo ci riconduce ai "Commenti sull'efficienza dell'algoritmo" del capitolo III. Cioè oltre un certo livello di potenza non si hanno più benefici sullo spettro. Infatti aumentando oltre lo 0.5% della potenza non si hanno più giovamenti. Ovviamente questo vale nel caso particolare di 64 sottoportanti di cui 4CCs. Cambiando i valori anche i risultati variano, poiché varia la matrice C che viene elaborata dall'algoritmo e quindi i valori singolari della decomposizione SVD (cap.III.5 Commenti sulla efficienza dell'algoritmo)
3 Validazione dei risultati forniti in letteratura
Un elemento di partenza per la sperimentazione era il riferimento [5]. Per avere la conferma che il nostro algoritmo funzionasse come richiesto abbiamo ricreato la condizione in [3].
Abbiamo supposto di avere un totale di 64 sottoportanti, ognuna delle quali trasporta un simbolo pari ad 1. Delle 64 sottoportanti 6 erano CCs, quindi le portanti dati erano in totale 58.
Come descritto precedentemente è stato calcolato lo spettro come sommatoria di sinc, quindi è stato stabilito un range di ottimizzazione e su questo è stato applicato l'algoritmo.
In letteratura sono forniti dati in condizioni ideali. La potenza dell'algoritmo viene testata senza modulazione, cioè trasmettendo sulle sottoportanti simboli pari ad 1.
Abbiamo adattato la simulazione al caso di 64 sottoportanti (58 dati e 6 CCs), quindi abbiamo graficato gli spettri.
I risultati forniti sono in termini di densità spettrale di potenza. Cerchiamo di mettere a confronto i risultati ottenuti con il nostro algoritmo e quello proposto in letteratura.
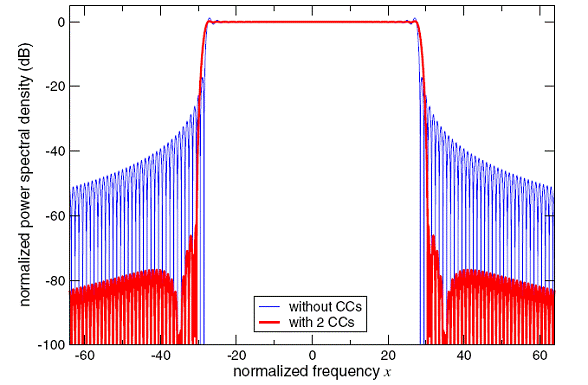
Fig. 8
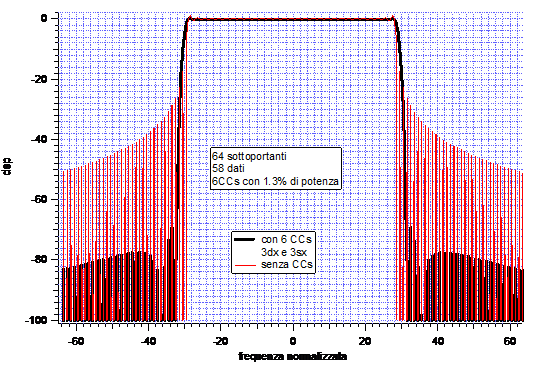
Fig.9
Vedendo i risultati delle simulazioni possiamo affermare che l'algoritmo implementato lavora come quello proposto in letteratura.
Una volta presa visione di questo lo applichiamo al nostro simulatore e cerchiamo di adattarlo ai nostri scopi.
Nel caso particolare del nostro simulatore gli spettri non sono stati calcolati come sommatoria di sinc poiché il modello di segnale è diverso. In un sistema simulato, dobbiamo tenere conto che il segnale deve essere sovracampionato nel tempo di un certo fattore L, inoltre noi non usiamo degli impulsi rettangolari nel tempo, ma RRCR con un certo fattore di rolloff, quindi lo spettro su cui andiamo ad applicare l'algoritmo di minimizzazione non sarà dato dalla somma di sinc.
Il modello del segnale a tempo continuo risulta:
![]() con
con ![]() e
e ![]()
Il segnale deve essere sovracampionato nel tempo con un certo fattore L, quindi
![]() passando al dominio
della frequenza otteniamo
passando al dominio
della frequenza otteniamo
![]()
![]()
![]()
Consideriamo ![]() dove k è l'indice della portante k-esima che contribuisce a
formare lo spettro.
dove k è l'indice della portante k-esima che contribuisce a
formare lo spettro.
Sviluppando in serie
di Taylor la sommatoria ![]() si ottiene:
si ottiene:
![]()
![]()


Con ![]()
Lo spettro delle
Cancellation Carriers si calcola allo stesso modo, usando i ![]() anziché gli
anziché gli ![]() che sono i simboli in
ingresso al convertitore serie/parallelo. Dall'algoritmo di minimizzazione
usciranno i valori delle incognite
che sono i simboli in
ingresso al convertitore serie/parallelo. Dall'algoritmo di minimizzazione
usciranno i valori delle incognite ![]() .
.
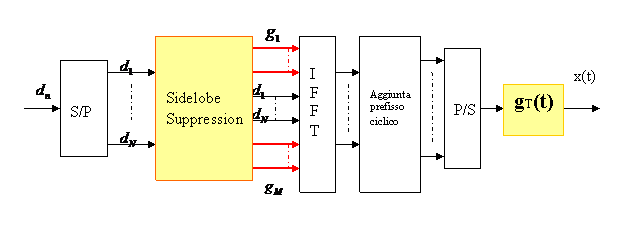
Fig. 10 schema a blocchi del trasmettitore OFDM
I risultati delle simulazioni sono riportati nel capitolo successivo
 |
| Appunti su: |
|
| Appunti Statistica |  |
| Tesine Geografia |  |
| Lezioni Contabilita |  |