 |
|
| Appunti scientifiche |
|
|
|
| Appunti scientifiche |
|
| Visite: 1857 | Gradito: |   [ Picolo appunti ] |
Leggi anche appunti:Le geometrie non euclideeLe geometrie non euclidee Il problema delle geometrie non euclidee e la rivoluzione La Sezione Aurea - Tra Matematica, Arte e NaturaLa Sezione Aurea Tra Matematica, Arte e Natura A coloro Limite di una funzioneLimite di una funzione Per introdurre il concetto di limite di una funzione |
 |
 |
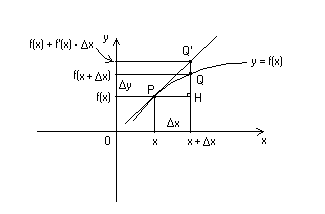
Consideriamo il grafico in figura che rappresenta la funzione f(x) e la sua tangente nel punto P[x ; f(x)].
Sia Q un punto della funzione di coordinate [x+x ; f(x+x)].
Osserviamo quindi che y = f(x+x)-f(x) = QH (1)
Analizziamo ora il triangolo rettangolo PHQ'. In esso sarà Q'H = PH tgα (2).
Ricordando la derivata ed il suo significato geometrico, la (2) può essere riscritta come Q'H = x f '(x), e cioé Q'H = df(x) = dy.
Geometricamente, quindi, il differenziale è la misura del segmento Q'H .
|
| Appunti su: significato geometrico del differenziale, |
|
| Appunti Geografia |  |
| Tesine Statistica |  |
| Lezioni Fisica |  |