 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1604 | Gradito: |
Leggi anche appunti:Risoluzione delle equazioniRisoluzione delle equazioni Per la risoluzione di un'equazione algebrica, Studio del diagramma di una funzioneSTUDIO DEL DIAGRAMMA DI UNA FUNZIONE I risultati fin qui ottenuti ci L'infinito matematicoL'INFINITO MATEMATICO 1.1.Il calcolo sublime L'origine del concetto matematico |
 |
 |
L'origine del concetto matematico di limite è da ricercarsi nella Magna Grecia, intorno al VI secolo a.C. più precisamente nella leggenda di Ippaso. Costui, allievo della scuola pitagorica, fu precipitato in mare dall'ira divina per aver violato il sacro vincolo della segretezza su quella che viene attualmente considerata la scoperta più importante dei Pitagorici: non il famoso teorema di Pitagora, già noto dagli Egizi, bensì i numeri irrazionali. I numeri irrazionali e di conseguenza l'incalcolabilità della √2, generavano il problema di segmenti costituito da un'infinità di punti: in che modo si doveva interpretare questa infinita divisibilità? Fu Zenone, membro della scuola eleatica, a fornire una risposta categorica. Nei suoi Argomenti contro il moto, Zenone afferma che data una distanza infinitamente divisibile tra due punti, risulta impossibile spostarsi dal primo al secondo in quanto ciò comporterebbe un tempo infinito. Pertanto il piè veloce Achille non potrà mai raggiungere la ben più lenta tartaruga.
A tali ragionamenti, che si presentavano come specchio della cultura filosofica ellenica del tempo, si deve la connotazione di base che sta alle origini della formulazione del concetto di limite. Circa 50 anni più tardi, veniva elaborato un metodo di calcolo del limite (peraV) detto di esaustione che trova una sua applicazione nel XII libro degli elementi di Euclide, in varie opere scritte da filosofi quali Platone e Aristotele, ma può essere attribuito solamente in via ipotetica a Eudosso di Cnido[1].
Il metodo di esaustione permetteva di trovare aree o volumi di regioni curve mediante approssimazione successive con l'uso di poligoni (o poliedri) iscritti e circoscritti dei quali le aree (o i volumi) erano note.
Un altro matematico che riveste una grande importanza nello studio dei limiti matematici è Archimede. Questi intorno al 225 a.C. vi fornì un importante contributo attraverso lo studio delle successioni aritmetiche continue. Servendosi del metodo di esaustione, Archimede studiò le aree di superfici curve più complesse (segmento parabolico, ellisse). Dimostrò, ad esempio, che l'area delimitata da un segmento di parabola corrisponde ai 4/3 dell'area di un triangolo costruito sullo stesso segmento e sul vertice della parabola, e ai 2/3 dell'area del parallelogramma ad esso circoscritto.
I lavori di Archimede furono dimenticati per oltre duemila anni e si ricostituirono solo a partire dal 1600. Tra i maggiori continuatori possiamo ricordare Bonaventura Cavalieri. Egli, allo stesso modo di quanto fatto da Archimede nel Metodo (testo ritrovato a Istanbul solo nel 1906), considera un'area come costituita da un numero indefinito di segmenti paralleli equidistanti e un volume come composto da un numero indefinito di aree piane parallele; questi elementi sono detti rispettivamente indivisibili di area e di volume (i moderni infinitesimi). Come semplificazione consideriamo il triangolo di figura:
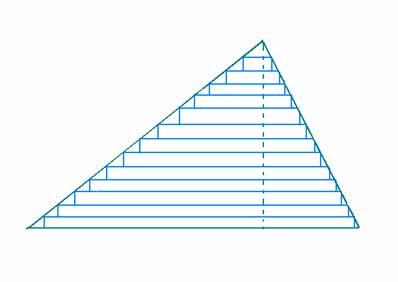
Figura - Metodo di esaustione applicato ad un triangolo scaleno
Esso è tagliato in tante strisce parallele. L'area del triangolo è il limite a cui tende lo scaloide inscritto quando il numero n delle strisce tende ad infinito. Per calcolare questo limite occorre conoscere la formula che dà la somma dei primi n numeri naturali (1+2+3+.+n = n(n+1)/2).
 Tuttavia risulta inevitabile e, anzi, necessario compiere un salto di
diversi secoli prima di giungere a risultati realmente soddisfacenti e
anticipatori della teorizzazione più coerente e completa del calcolo dei
limiti: quella alla quale giunsero, separatamente ma nella stessa epoca
storica, Leibniz e Newton.
Tuttavia risulta inevitabile e, anzi, necessario compiere un salto di
diversi secoli prima di giungere a risultati realmente soddisfacenti e
anticipatori della teorizzazione più coerente e completa del calcolo dei
limiti: quella alla quale giunsero, separatamente ma nella stessa epoca
storica, Leibniz e Newton.
Malgrado numerosi dibattiti, non si è ancora giunti a stabilire chi dei due conseguì prima i suoi risultati. Tuttavia la critica moderna riconosce una formale precedenza a Leibniz che espresse i suoi risultati nell'articolo Nova Methodus pro Maxima et Minimi (itemque tangentibus, quae nec fractas nec irrationales quantitates moratur, et singulare pro illis calculi genus) pubblicato sugli Acta Eruditorum nel 1684 ossia ben tre anni
Figura - Ritratto di Gottfried Wilhelm Leibniz
prima dei Philosophiae Naturalis Principia Matematica newtoniani.
Sin dagli appunti che tale studioso compose prima dell'articolo suddetto, si rileva all'interno della sua speculazione la centralità del problema di trovare le tangenti alle curve (definizione di derivata), inteso direttamente oppure inversamente, ossia come ricerca delle aree e dei volumi per sommazione. Questo concetto era espresso dalla conclusione che "l'integrazione come procedimento di sommazione è l'inverso della differenziazione"
Senza avere un concetto chiaro di area (delimitata da una
curva su un piano cartesiano), Leibniz 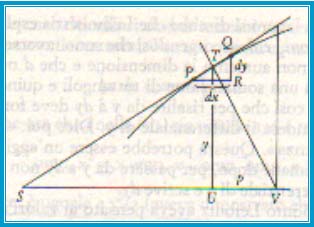 intendeva quest'ultima come somma di numerosi rettangoli molto piccoli
e la differenza fra tale somma e la superficie reale come trascurabile. Oltre
alla sostanziale ripresa del metodo greco di esaustione, notiamo qui anche un
importante elemento innovativo: la definizione di dx e dy come quantità
arbitrariamente piccole e tali che il loro rapporto costituisse la derivata
alla curva nel punto P(x,y), vale a dire la tangente alla curva stessa in quel
punto (come mostra l'immagine a lato).
intendeva quest'ultima come somma di numerosi rettangoli molto piccoli
e la differenza fra tale somma e la superficie reale come trascurabile. Oltre
alla sostanziale ripresa del metodo greco di esaustione, notiamo qui anche un
importante elemento innovativo: la definizione di dx e dy come quantità
arbitrariamente piccole e tali che il loro rapporto costituisse la derivata
alla curva nel punto P(x,y), vale a dire la tangente alla curva stessa in quel
punto (come mostra l'immagine a lato).
Figura - Tangente a una curva
L'articolo contenuto negli Acta eruditorum inizia proprio con la descrizione delle regole di derivazione.
Sebbene nell'elaborazione dell'articolo in questione Leibniz si limiti alla presentazione del solo calcolo differenziale (df (x)/dx), la corrispondenza intrattenuta con Newton durante gli anni precedenti, ci dimostra che egli era in possesso anche delle idee fondamentali dell'aspetto inverso, ossia del calcolo integrale ( f(x)dx).
L'importanza dell'opera di Leibniz nel campo dell'analisi matematica e, quindi, della nascita del calcolo infinitesimale, è generalmente individuata dai critici nella sua attenzione al problema della notazione: ancora attualmente, infatti, si usa indicare le derivate con dx, dy e dx/dy, e gli integrali con il segno ∫ (il simbolo ∫ è la stilizzazione di S, che è l'iniziale di somma). Leibniz, infatti, aveva compreso l'importanza di una simbologia chiara. Nel 1686 scriveva: "Raccomando di non omettere dx, errore frequentemente commesso e che impedisce di andare più oltre". Inoltre poneva i fattori costanti fuori del segno di integrale e determinando che la somma di due integrali è uguale all'integrale della somma. Nel 1694 definisce il concetto di funzione: "Si dice che y è funzione di x, quando a certi valori di x corrispondono valori determinati di y". Fu sempre egli ad introdurre la dizione di "calculus differentialis", quello che permetteva di trovare le tangenti e di "calculus integralis" che realizzava le quadrature (calcolo di area o volume). L'esposizione più organica del calcolo infinitesimale di Leibniz fu data nel 1684 con l'articolo già citato Nova Methodus pro Maxima et Minimi.
 Meno 'universale' rispetto a Leibniz ma, forse, più
'geniale' si rivelò l'opera di Sir Isaac Newton.
Meno 'universale' rispetto a Leibniz ma, forse, più
'geniale' si rivelò l'opera di Sir Isaac Newton.
Il suo capolavoro Philosophiae naturalis Principia mathematica, come precedentemente ricordato, uscì nel 1687. L'introduzione al primo libro conteneva alcuni teoremi sul calcolo infinitesimale, che già erano stati affidati a tre redazioni precedenti: quella del De analysi per aequationes numero terminorum infinitas, composta nel 1669, ma pubblicata solo nel 1711, quella della Methodus fluxionum et serierum infinitarum (in cui compare la terminologia e la notazione tipica delle flussioni), redatta nel 1671 e pubblicata nel 1742, e quella
Figura - Ritratto di Isaac Newton
del De quadratura curvarum (in cui si trova Metodo delle prime ed ultime ragioni[2] col cui aiuto si dimostra le cose che seguono).
Newton generalizzò le idee sul calcolo infinitesimale già presenti nei matematici a lui precedenti, e le caratterizzò mediante metodi pienamente maturi. Non riuscì però a fornire una notazione rigorosa, in quanto maggiormente interessato alle loro applicazioni pratiche, in particolare nell'ambito della fisica.
È certo che la struttura del calcolo di Leibniz e Newton era carente. Ci sono voluti almeno altri cento anni affinché la matematica acquistasse il rigore necessario con l'opera di Lagrange[3] prima (1797) e di Cauchy poi (1829).
Come avviene per altri concetti fondamentali quali lo spazio e il tempo, il concetto di numero sembra abbastanza difficile da definire. Alla domanda "Che cos'è il numero?", il logico Frege rispondeva: "È una cosa!"
La voce di Frege si inseriva nel dibattito attorno al concetto di numero naturale che ha impegnato i più grandi matematici di fine Ottocento. Secondo il matematico Von Helmholtz, l'aritmetica è fondata su fatti puramente psicologici. Secondo Frege l'aritmetica non ha nulla a che vedere con le sensazioni e con le immagini interne ma è una logica sviluppata. Secondo Dedekind, ancora, i numeri sono libere creazioni del pensiero umano, di cui studia le proprietà.
Per Dedekind la scienza dei numeri si basa sulla capacità della mente di mettere in relazione un oggetto con un altro oggetto. Per caratterizzare la successione dei numeri naturali, Dedekind utilizza la nozione primitiva di insieme di oggetti e di corrispondenza univoca tra insiemi. Egli privilegia l'aspetto ordinale del concetto di numero naturale (1,2,3). Attraverso la nozione di sistema, egli costruisce la successione dei numeri naturali in forma assiomatica[4]. Quando si parla di successione dei numeri un concetto è fondamentale: quello di infinito. La successione numerica non ha termine. Infatti, dopo un numero n grande si può sempre considerare il numero successivo n+1: la successione dei numeri naturali offre l'esempio più semplice di infinito matematico. Come avrebbe detto Aristotele, si tratta di un infinito in potenza per distinguerlo dall'infinito in atto come quello del continuo matematico. Senza infinito non si hanno i numeri naturali e non si fa un passo in matematica."Da sempre l'infinito ha eccitato l'animo umano; ma l'infinito e un'astrazione spaventosa che senza speciali precauzioni non è ammissibile nemmeno in matematica. Non proviene dall'esperienza, ma si presenta alla mente non appena essa tenta di formalizzare in termini matematici l'esperienza" (David Hilbert). L'infinito è un prodotto della mente.
Ma l'infinito potenziale può manifestarsi in forme meno elementari come nel caso dei numeri razionali. Infatti, l'insieme dei numeri razionali è un insieme denso: tra due numeri razionali, per quanto vicini, ce ne sono infiniti maggiori del più piccolo e minori del più grande Ad esempio, sono infiniti i numeri razionali compresi tra 0 ed 1 che sono tutte frazioni che hanno il numeratore più piccolo del denominatore. Se poi consideriamo, il segmento di estremi 0 ed 1 ed associamo ogni frazione tra essi compresa ad un punto di tale segmento, possiamo osservare che tali frazioni rappresentano infinite divisioni del suddetto segmento.
Prima di Pitagora, i greci avevano la convinzione che tutti i rapporti di due misure potessero venire scritti come una frazione: 3/4, 9/1, 355/113 (numeri razionali).
L'infinito potenziale espresso dai numeri razionali è perciò un infinito ottenuto per divisione. La caratteristica di tale infinito è che esso è interamente contenuto in una totalità limitata: dividendo all'infinito un segmento in parti sempre più piccole, risulta evidente che tutti gli elementi della divisione sono in realtà già assegnati e presenti, prima ancora che la stessa divisione abbia inizio; appartenendo ad una forma limitata essi non possono sfuggire e non possono che essere ritrovati durante un processo all'infinito che inevitabilmente li raggiunge tutti.
L'applicazione del teorema di Pitagora a un triangolo isoscele rettangolo mise in evidenza che il rapporto lato/diagonale (√2) non poteva mai essere espresso sotto forma di numero frazionario; servirebbe, infatti, un numero infinito di cifre sia al numeratore che al denominatore. Viene posto così il problema di un nuovo tipo di numero che non è razionale, cioè rappresentabile come frazione: il numero irrazionale.
In pochi anni la trattazione dell'infinito cambia completamente. Il merito va al matematico Georg Cantor. Egli ribalta il punto di vista mantenuto per oltre duemila anni, rivalutando il concetto di infinito attuale. L'idea dominante fino a Cantor è che se l'infinito esiste allora è unico e insuperabile. Cantor dimostrò invece che non si poteva semplicemente parlare di un infinito ma che bisognava parlare di infiniti infiniti e soprattutto di infiniti più grandi e di infiniti più piccoli. Cantor, nel 1873, fece fare un passo avanti al pensiero matematico e filosofico provando l'esistenza dell'infinito attuale transfinito, sempre accrescibile. Infatti, egli dimostrò, per esempio, che l'insieme dei punti di un segmento, ovvero l'insieme dei numeri reali R non è numerabile[5]; più in generale, nel 1891, Cantor riuscì a dimostrare l'esistenza di infiniti numeri transfiniti maggiori di X (alef con zero), ovvero per ogni insieme infinito se ne può trovare un altro che ha un numero di elementi maggiore.
Eudosso di Cnido (410-356 a.C.), coetaneo e amico di Platone. Per i suoi studi sulla teoria delle proporzioni e sulla teoria dei rapporti irrazionali, Eudosso deve essere riguardato come uno dei più sottili matematici dell'antichità, precursore nell'uso dei limiti e nell'introduzione del calcolo infinitesimale.
Giuseppe Luigi Lagrange (1736-1813) compì studi fondamentali in svariati ambiti della matematica e della meccanica celeste. Si occupò anche dell'elaborazione del procedimento del calcolo delle derivate.
 |
| Appunti su: |
|
| Appunti Statistica |  |
| Tesine Geografia |  |
| Lezioni Fisica |  |