 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3119 | Gradito: |
Leggi anche appunti:Il calcolatore universaleIl calcolatore universale Nasce il 1° AGOSTO 1945 'MARK 1'. (ufficialmente Spazi vettorialiSPAZI VETTORIALI Siano K un campo e V un insieme. Diremo che V e` uno spazio Teorema sul limite delle funzioni composteTEOREMA SUL LIMITE DELLE FUNZIONI COMPOSTE E' molto importante per le applicazioni |
 |
 |
MATEMATICA:
C'E' UNA COSA DI CUI I "NON MATEMATICI" NON SI RENDONO CONTO, ED E' CHE LA MATEMATICA E' IN REALTA' QUASI INTERAMENTE UN SOGGETTO ESTETICO.
John Conway
La discussione sull'aspetto estetico della matematica ha da sempre interessato gli appassionati e in particolare i matematici stessi.
Infatti, coloro che vedono la matematica solamente come una scienza esatta, scienza dell'ordine e dell'analisi, non si riescono a soffermare sull'aspetto più affascinante di questa disciplina.
La matematica è fatta di numeri e tra questi un piccolo gruppo attira l'attenzione di molti, fin dalla loro scoperta.
Un esempio fra tutti è il valore di π che lega la circonferenza al proprio diametro.
Quello che più interessa di questo numero è il suo essere irrazionale, cioè non rappresentabile attraverso una frazione, rendendo quindi diametro e circonferenza incommensurabili tra loro.
Un numero meno conosciuto, ma con caratteristiche altrettanto peculiari è il meno noto Φ.
Questo valore, conosciuto fin dall'epoca classica, è il numero irrazionale (√5+1)/2 che si diceva generare la divina proporzione, e a cui si attribuivano particolari proprietà estetiche.
Quando usiamo il termine proporzione vogliamo indicare un rapporto tra cose caratterizzato da una particolare armonia; diversamente però viene utilizzato in matematica dove proporzione è l'uguaglianza tra due rapporti. Nel caso della divina proporzione, significato estetico e quantitativo diventano un'unica realtà.
Questo numero, per certi versi anche molto misterioso, acquisì nel Rinascimento la denominazione di gioiello della geometria da Keplero e più recentemente anche il nome di numero aureo, rapporto aureo e sezione aurea.
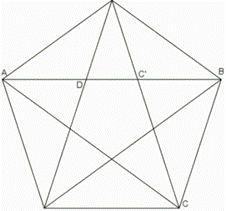
Ancora più interessante appare la determinazione di tale rapporto anche in altre figure geometriche come il pentagono equilatero ed equiangolo, dove le diagonali di due angoli consecutivi intercettano parti (a due a due congruenti) che stanno tra loro in rapporto aureo. Dato che la parte maggiore è anche pari al lato del pentagono, si può anche dire che la diagonale del pentagono è pari al prodotto del lato per il rapporto aureo.
Anche nel pentagramma, cioè la stella a 5 punte che si può disegnare dentro al pentagono, si può rintracciare un rapporto aureo: infatti in ciascuno dei triangoli isosceli che formano le punte, il rapporto tra uno dei due lati e l'ipotetica base è proprio Φ!
AB:AC'=AC':C'B → AB/AC'= Φ
AC'=BC → AB/BC = Φ
Inoltre:
BC'/C'D = Φ
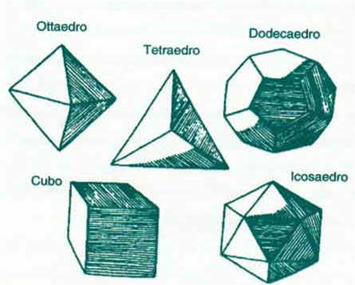
Ma da quello che si sa, fu Euclide il primo a fornire una definizione vera e propria del numero aureo di cui poi si servì per costruire i 5 solidi regolari, definiti platonici. Tali figure geometriche, oltre ad essere gli unici solidi esistenti che contengono solo facce regolari e uguali tra loro, sono state considerate per secoli dotate di eccezionali proprietà naturali ed estetiche, convinzione accresciuta dal fatto che hanno uno stretto rapporto con il numero aureo.
Ma al di là di queste considerazioni geometriche, è bello capire dove e come anche grandi artisti hanno sfruttato la sezione aurea.
Se alcuni studiosi, convinti che già il Partenone si rifacesse al rapporto aureo, sono stati screditati, è invece sicuro che artisti come Dalì e Le Corbusier si sono serviti della divina proporzione per modelli o opere.
Infatti Dalì dà al dipinto il 'Sacramento dell'Ultima Cena' delle dimensioni il cui rapporto si avvicina moltissimo a quello aureo, ma soprattutto vi inserisce la figura di un dodecaedro che domina la scena, forse ricordando il ruolo che Platone attribuiva a questa figura: cioè la forma usata dalla divinità per ricamare le costellazioni sull'insieme dei cieli.

Le Corbusier invece, alla ricerca di un'idea universale di bellezza, iniziò a cercare una proporzione standard che chiamò 'modulor', la quale doveva fornire 'una misura armonica della scala umana universalmente applicabile all'architettura e alla meccanica'.
Una figura umana alta circa 183 centimetri e con un braccio alzato fu inserita in un quadrato e ne vennero stabilite le dimensioni parziali. Risultato: il rapporto fra l'altezza dell'uomo e l'altezza del suo ombelico risulta esattamente uguale a φ e calcolando la sezione aurea dell'altezza totale (ovvero dalla mano alzata a terra) si vede che coincide esattamente con il polso dell'uomo.
In realtà sembra essere stata la natura la prima ad applicare alle sue opere proprio il rapporto aureo.
Osservando la disposizione delle foglie sui rami o dei petali di un fiore ad esempio, possiamo notare che spesso ricorre una successione numerica molto famosa: la successione di Fibonacci.
Tale semplice successione prevede che ogni suo numero sia la somma de due precedenti, supposto che i primi siano entrambi 1.
Da cui si ricava la formula: Fn = Fn-1 + Fn-2 e quindi comincia con 1 1 2 3 5 8 13 21 34 55 89..
Tale successione si può ritrovare, come accennato sopra, nella disposizione delle foglie sui rami detta fillotassi:
alle volte le foglie si dispongono da due parti opposte, avendo così un "quoziente di fillotassi" pari a ½.
In altre piante il passaggio da una foglia all'altra comporta un terzo di giro, in altre ancora tre ottavi.
Perciò tutti i rapporti si dimostrano essere frazioni di termini alternati della successione.
Di esempi a proposito della fillotassi ce ne sarebbero ancora parecchi, però quello che ora ci interessa notare è il rapporto che lega la successione al numero aureo e quindi questo alla natura.
proprio a Φ!
Quindi lim n→∞ Fn / Fn-1 = Φ.
La spiegazione di questa relazione è da ricercarsi nell'equazione in cui si può
![]() altrimenti scrivere
il rapporto aureo: x = 1+ 1
altrimenti scrivere
il rapporto aureo: x = 1+ 1
1+ 1
![]() 1+ 1
1+ 1
![]() 1+ .
1+ .
Tra l'altro, proprio da questa relazione, che possiamo scrivere come
x = 1 + 1/x oppure x2 = x + 1 , possiamo ottenere bellissimi risultati.
Innanzitutto la spirale logaritmica ha origine da un 'rettangolo aureo', ovvero un rettangolo le cui dimensioni siano in rapporto aureo.
Se si traccia un segmento parallelo al lato 'corto' del rettangolo in modo tale da ottenere un quadrato, il rettangolo che resta è ancora un rettangolo aureo, ovvero il segmento tracciato divide il lato lungo del rettangolo in due segmenti che sono in proporzione aurea e sono separati da un 'punto aureo'. Facendo la stessa operazione con questo rettangolo più piccolo si ottiene un nuovo quadrato, un nuovo rettangolo aureo e due nuovi punti aurei. Immaginiamo di andare avanti 'all'infinito' e di unire i punti aurei (seguendo ad esempio il verso orario) con un curva che sia ogni volta tangente al segmento che tocca nel punto aureo.
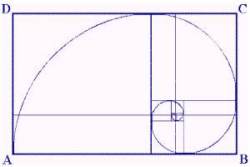
Questa figura è caratterizzata dall'auto-similitudine, nel senso che ingrandita o rimpicciolita ha sempre le medesime caratteristiche.
Ma questa è la stessa definizione che possiamo dare ai frattali: oggetti in cui lo stesso schema si riproduce in miniatura all'interno di se stesso.
I frattali sono delle strutture che si possono trovare in natura molto più frequentemente di oggetti che riportino strutture semplice che le normali figure geometriche che siamo soliti studiare.
Il primo grande studioso dei frattali fu Mandelbrot che ebbe la grande intuizione partendo dall'analisi di oggetti naturali i cui contorni via via che si rimpicciolisce la scala presentano le stesse strutture che si erano osservate con una scala maggiore.
Uno dei primi "problemi" affrontati dal matematico fu la misurazione delle coste della Gran Bretagna.
Egli espose la teoria secondo cui la lunghezza delle coste andrebbe via via aumentando con la diminuzione dello strumento di misurazione.
Da ciò quindi si otterrebbe lo strano fenomeno di una figura con perimetro infinito ma area definita e costante.
La sua teoria può essere semplificata prendendo ad esempio il triangolo di Koch:

da cui ha origine la bellissima immagine del fiocco di neve.
Per ottenerlo si parte da un triangolo equilatero, al centro di ogni lato si costruisce un triangolo più piccolo con un lato pari a 1/3 del lato di partenza. Procedendo così per ciascuna punta della stella di David ottenuta, all'infinito, si otterrà una figura sempre più complessa.
A parte la crescente complessità, è da notare come il perimetro abbia formula: 2P = 3a (4/3)n e quindi quando n tende ad infinito lo stesso perimetro tenderà ad infinito.
Al contrario invece con una più complessa formula si può ottenere la dimensione dell'area che tende a 8/5 dell'area del triangolo di partenza.
Da queste scoperte si è arrivati a determinare la diffusione in natura di queste figure frattali di cui l'insieme di Mandelbrot è uno degli esempi più noti.
Ovviamente non si esaurisce qui il discorso sulla bellezza matematica. Ci sarebbero ancora infiniti esempi che cercano di indagare nel mistero della matematica e scoprirebbero altre meraviglie.
ARTE: "l'estetica neoclassica"
Se della matematica risulta talvolta difficile accettare che si occupi della ricerca del lato estetico, ancor prima di quello utilitaristico, funzionale o teoretico; nell'arte nessuno si giustificherebbe, al contrario, la mancanza del culto della bellezza quale principale obiettivo.
Il Seicento era stato caratterizzato da un'arte che aveva l'ambizioso traguardo di persuadere eretici e dubbiosi riconducendoli alla dottrina cattolica. Per raggiungere questo scopo la Chiesa si servì di un'arte che si mostrasse in tutta la sua grandiosità: il Barocco. Soprattutto in pittura e scultura quest'arte arrivò agli estremi tanto da rasentare la sdolcinatura e la frivolezza; in architettura invece era obiettivo primario la monumentalità e la forma, cioè la decorazione, ancor prima della funzione.
Ben presto superato questo periodo di eccessi, gli artisti sentirono la necessità di tornare a forme e regole che si rifacessero ai principi classici. Questo significava tornare a seguire canoni che avrebbero portato alla definizione del BELLO IDEALE proposto due millenni prima da greci e romani.
Non era quindi concesso trasportare nelle opere le proprie emozioni, i propri ideali: era invece fondamentale rispettare e imitare la grandezza artistica degli antichi.
Il massimo teorico del movimento neoclassico fu senza dubbio Johann Joachim Winckelmann. Sebbene lontano dagli esempi dell'arte greca, di cui tra l'altro aveva potuto ammirare solo copie romane, pubblicò "Pensieri sull'imitazione dell'arte greca nella pittura e nella scultura" in cui erano presenti già tutti i temi dell'arte neoclassica.
I sui principi, sviluppati attorno all'espressione "nobile semplicità e quieta grandezza", proponevano l'imitazione della sola arte greca: questo significava non eseguire un'opera come semplice copia dell'originale, finendo per non creare nulla di nuovo; ma invece ispirarsi ad un modello che si cerca di eguagliare.
Così com'era stato nel passato, anche ora le figure rappresentate, per quanto agitate da passioni, dovevano mostrare un animo posato. Dicendo che "più tranquilla è la posizione del corpo e più in grado è di esprimere il vero carattere dell'anima", Winckelmann stabiliva la necessità di scegliere di rappresentare sempre il momento che precede o segue un'azione tragica, quando il tumulto delle passioni o non c'è ancora o si è già attenuato.
Le teorie winckemanniane vennero subito incarnate da un celebre artista che visse a cavallo del XVIII e XIX secolo: Antonio Canova.
Canova, che nacque nel 1757 nei pressi di Treviso, si trasferì a soli 22 anni nella capitale dove inizialmente frequentò l'Accademia di Francia. Salvo alcuni viaggi all'estero, o in veste di ambasciatore per ottenere la restituzione di opere sottratte da Napoleone, o per poter ammirare resti dell'antichità classica nei più grandi musei europei, rimase per tutta la vita a Roma.
La vasta produzione del Canova comprende moltissime sculture, ma soprattutto un largo numero di disegni, utili a costruire una casistica quanto più ampia possibile di atteggiamenti, posizioni ed espressioni.
Ed è già in questi numerosi bozzetti che l'artista mostra le sue grandi doti, ma in particolare i suoi studi per comprendere i rapporti proporzionali fra le parti e il tutto: una tavola pitagorica di regole e di proporzioni; tutta un insieme di rigide norme contro l'evoluzione della storia, con l'unico obiettivo di raggiungere l'armonia.
Ai lati, come era sua abitudine, sono riportate alcune cifre: misure delle proporzioni per la realizzazione della scultura.
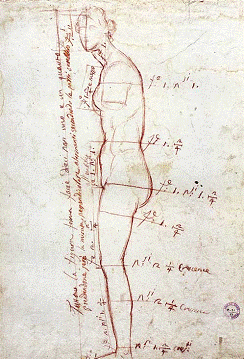

Ma è proprio la scultura che in epoca neoclassica assume un ruolo primario: perché era l'arte con cui più facilmente si poteva raggiungere l'ideale di bellezza raggiunto dai Greci. Canova esegue infatti numerose opere attenendosi alle teorie del Winckelmann con l'obiettivo di realizzare l'idea di "bello" che si forma nell'idea dell'artista visto che in natura è assente.
Quindi vengono rappresentati eroi nei momenti successivi al combattimento, amanti nell'attimo prima di un atto d'amore: i corpi dei protagonisti infatti sono sempre distesi perché non più o non ancora preda delle forti passioni.
guardata solo frontalmente, ma per
apprezzare i diversi rapporti tra i corpi nello spazio, e quindi girandovi
attorno.

Con l'obiettivo di rendere viva la scultura Canova ricoprì di una cera rosata le sue sculture. Essendo oggi andata perduta dopo un restauro, la statua sembra ancora più fredda e intenta unicamente a ottenere la perfezione.

Questa volta il momento rappresentato non precede né segue una forte passione.
Le tre figure femminili sono cinte da un velo che rafforza il senso di unione dettato dall'abbraccio della figura centrale.
Come base d'appoggio, le figure si reggono su una colonna che funge da altare. Come nelle altre opere di Canova, la sinuosità delle forme femminili, la delicatezza e la morbidezza ottenute con la ricercata levigatezza del marmo determinano un particolare gioco di luci ed ombre.
Questa volta il momento rappresentato non precede né segue una forte passione.
Le tre figure femminili sono cinte da un velo che rafforza il senso di unione dettato dall'abbraccio della figura centrale.
Come base d'appoggio, le figure si reggono su una colonna che funge da altare. Come nelle altre opere di Canova, la sinuosità delle forme femminili, la delicatezza e la morbidezza ottenute con la ricercata levigatezza del marmo determinano un particolare gioco di luci ed ombre.

Come nell'arte classica, Canova cura nel dettaglio la muscolatura , creando un corpo perfettamente proporzionato. Inoltre riprende il tipico chiasmo, facendo perciò corrispondere al braccio destro in tensione la gamba sinistra ugualmente tesa e gli arti posti sull'asse speculare in movimento.

FILOSOFIA: SCHOPENHAUER E L'ARTE COME OGGETTIVAZIONE DELLA VOLONTA'
E' proprio l'arte che all'interno del pensiero di Schopenhauer svolge un ruolo fondamentale. La sua filosofia è il risultato di una ripresa kantiana del pensiero. Essa ruota attorno al concetto di volontà, che finisce per coincidere con il noumeno. La volontà è il principio che muove il vivente ed è volta all'esclusiva affermazione di sé. Essa è sempre una in sé e differisce dal suo fenomeno. E' in questo che la volontà si dà come volontà determinata: essa è assoggettata al principio di ragion sufficiente, in quanto appare secondo le categorie di spazio e tempo. Proprio a causa di queste la volontà ci appare in modi e quantità diversi, producendo quindi le rappresentazioni. Queste sono il corrispondente dei fenomeni kantiani, che per Schopenhauer sono gli unici costituenti del mondo, che quindi è solo apparenza ed illusione. Trascendendo il fenomeno si può accedere al noumeno che si nasconde dietro il velo di Maya. Nel percorso di oggettivazione della volontà, proposto da Schopenhauer , la riflessione sull'arte costituisce il culmine. Al contrario di tutti I rami del sapere, l'arte è l'unico non soggetto al principio di ragion sufficiente, e quindi consente di trascendere l'orizzonte del fenomenico.
Dal momento che gli oggetti dell'arte sono sottratti alle relazioni di spazio e tempo, l'arte può essere definita la contemplazione delle cose.
Ma come l'arte e I suoi oggetti sono liberi da ogni oggettivazione, così deve pur essere ciò che la produce: Essendo l'arte "opera del genio" la sua essenza consiste nella "straordinaria attitudine" alla contemplazione delle idee. Il genio è la più grande forma dell'oggettività, pertanto la sua conoscenza è diretta conoscenza delle idee. così, dopo l'introduzione dell'idea dell'arte, Schopenhauer propone l'esperienza del bello e del sublime per raggiungere l'annullamento della volontà individuale. Entrambe infatti, con metodi differenti giungono allo stesso risultato.
Il sublime inteso come lo spettacolo che la natura scatena, ci pone di fronte alla "sconfitta della nostra volontà".
Davanti agli sconvolgimenti della natura e pure alla grandezza dell'universo "ci sentiamo rimpiccioliti fino all'annullamento". Ma noi, sapendo che questi eventi hanno effetto sulla nostra individualità, sebbene siano mere rappresentazioni, ci accordiamo di non dipendere dalla grandezza della natura, che al contrario dipende da noi.
L'esperienza del bello invece procede dal soggetto in cui la volontà sparisce come un libero e cosciente sollevarsi. Giudichiamo bella una cosa la cui vista ci rende obiettivi, quindi quando si annulla la volontà individuale elevandoci a puri soggetti conoscenti, liberi da ogni volontà. Nell'oggetto bello riusciamo così ad individuare l'idea e la nostra contemplazione risiede direttamente nell'oggetto stesso.
ENGLISH: OSCAR WILDE AND THE FIGURE OF THE DANDY
Oscar Wilde was born in Dublin in 1854. He was the son of a well-known surgeon, Knighted by Queen Victoria, Sir William Wilde and a literary woman, Jane Elgee.He was educated at Dublin University's Trinity College where he proved to be a brilliant student of the Classics. Oscar could see it too, for this reason he thought that a talent as rare as his should not be consigned to a provincial college. Oxford, a school that could confer the prestige he thought he deserved, seemed a better choice. In his third year at Dublin, he competed for a scholarship at Oxford's Magdalen College and won.
Oscar arrived at Oxford in 1874 and quickly fell in with a new literary movement called aestheticism that was stirring controversy amongst the English literary set. The English aesthetic movement was calculated to shock the Victorian middle class by rejecting the popular notion that a work of literature should be a sort of sermon that serves some higher spiritual purpose. Walter Pater, a leader of the movement and one of Wilde's favorite professors, replaced Victorian middle class themes like authenticity, nature, and romance with artifice, sophisticated connoisseurship, and most subversively, individual pleasure.
Wilde took to aestheticism with the enthusiasm of a new convert, but he saw that his teacher Pater was more talk than action. In spite of Pater's disquisitions on beauty and pleasure, he lived an austere life. On the contrary, Wilde would live a life devoted to beauty and pleasure, a life that was itself a work of art. He started with a makeover. At a time when men's fashion favored dark suits and inconspicuous ties, Wilde covered his hands with flashy rings, wore a huge bow for a tie. Even though his outfits made him the object of jeers and insults, his new look succeeded in putting him at the center of attention, just where he wanted to be.
With this life style, like a "work of art", as he called it, he adopted the "aeshtetical ideal" and embodied the figure of the dandy: an aristocratic man whose elegance is a simbol of the superiority of the spirit.
Wilde's celebrity came unexpectedly from a satirical magazine, "Punch", which had published cartoons that poked fun at the London's literary dandies. George Du Maurier, the cartoonist, used Punch to express his distaste for what he saw as effeminacy and superficiality among the aesthetes. This made Wilde the public emblem of the aesthetic movement before he had even published a book.
In the beautiful social life he had in London, full of parties and meetings, he began to have homosexual affairs. Even though this caused him two years of hard labor in a prison, his new sexual inclinations provided an idea for a novel he was working on:The Picture of Dorian Gray.
In spite of the violent reaction aroused by the novel, it eventually became the Manifesto of English Aestheticism.
Written by anyone else, The Picture of Dorian Gray would have been read as a warning against aestheticism, but Wilde probably gave the title character a bad end to confuse his critics. Dorian is a beautiful young man who attracts men and women alike. One day while Basil Hallward, a painter who is homoerotically enraptured with Dorian, paints his portrait, Dorian meets Lord Henry Watton and becomes his close friend. Dorian wishes that he might retain his beauty, and that his portrait should bear the marks of age in his stead.
So, even though under Henry's influence Dorian rapidly deteriorates, driven by him to a life of pleasures and sensation, he retains his youth and beauty. But the more he degenerates, the more hideous the painting becomes. As it reveals his narcissistic soul in horrible details, he locks it away in a room.
At the age of 38, Dorian shows the portrait to Hallward, but realizing that he has actually revealed his inner self, he kills the painter. The book ends when Dorian slashes the portrait in a fit of rage and then dies because the painting no longer represents, but has become his wicked soul.
BIBLIOGRAFIA:
MATEMATICA:
- "La sezione aurea" di Mario Livio; ed. Rizzoli; anno 2005.
STORIA DELL'ARTE:
- "Itinerario nell'arte" di Cricco e Di Teodoro; ed. Zanichelli; anno 2005.
FILOSOFIA:
- "Argomentare" di Boniolo e Vidali; ed. Mondadori; anno 2005.
INGLESE:
-"Witness to the times" di Mingazzini e Salmoiraghi; ed. Principato; anno 2005.
 |
| Appunti su: bellezza rapporti matematici canova, |
|
| Appunti Fisica |  |
| Tesine Geografia |  |
| Lezioni Contabilita |  |