 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3367 | Gradito: |
Leggi anche appunti:Campo e bosone di higgsCAMPO E BOSONE DI HIGGS Noi sappiamo che tutte le cose che esistono, esistono MetrologiaMETROLOGIA La metrologia è la scienza che si occupa della misurazione delle Mars ExplorationsMars Explorations Marte, il Pianeta Rosso. Quarto pianeta del |
 |
 |
Teoria della relatività ristretta
Le radici della Relatività

La fisica, ancor prima delle rivoluzioni di Einstein, agli inizi del '900, aveva raggiunto una completezza ed una organicità tale, da considerarsi incrollabile, almeno nelle sue fondamenta.
La scienza più antica del mondo fino agli inizi del XX secolo era fondata sui principi della meccanica classica, enunciati nel XVII secolo da Isaac Newton, della cui teoria, ogni singola legge era stata continuamente corroborata con successo.
Il più importante assunto della fisica classica, dovuto a Galileo Galilei, è il principio della relatività galileiana definito nel 1609, cioè che le leggi della fisica devono avere la stessa forma rispetto a qualunque sistema di riferimento rettilineo ed uniforme. Esso si basa sulla grande intuizione di Galileo che considera gli spazi rispetto allo stesso evento, in relazione alla velocità del proprio sistema di riferimento, cioè due osservatori posti in moto uno rispetto all'altro misureranno spazi differenti. Nulla tuttavia si dice sui tempi.
Il postulato di Galileo si enuncia così:
"Le leggi fisiche sono le stesse in ogni sistema di riferimento inerziale quindi non esiste un sistema di riferimento privilegiato."
 Il
modello di Galileo era la base del sapere della fisica classica perché in esso
trovavano validità tutte le leggi della dinamica e della gravitazione di
Newton.
Il
modello di Galileo era la base del sapere della fisica classica perché in esso
trovavano validità tutte le leggi della dinamica e della gravitazione di
Newton.
Ma come si scoprì poi successivamente, tale principio era insufficiente fisicamente parlando, nell'inglobare anche le equazioni dell'elettromagnetismo formulata da Maxwell, della seconda metà dell'800, cioè le leggi elettromagnetiche non trovavano l'adeguato riscontro matematico nel principio di Galileo. Le intuizioni di Maxwell infatti sollevavano problemi e contraddizioni sconcertanti che scuotevano le basi della conoscenza fisica e persino del senso comune.
Ma la novità più "pericolosa" della nuova teoria della luce di Maxwell, è la velocità con cui le onde elettromagnetiche si propagano, ovvero "c". Infatti sorgeva spontanea la domanda: velocità c relativo a che cosa??
In conseguenza alla teoria di Fresnel (' 1817), fisico francese che fece importanti studi in campo ottico, e della verifica sperimentale di alcune sue previsioni, la comunità scientifica aveva accertato che la luce consistesse in un fenomeno ondulatorio e, in analogia con tutti i fenomeni ondulatori conosciuti all'epoca, sembrava perfettamente "naturale" ammettere che esistesse un mezzo materiale le cui vibrazioni costituissero la luce.
Ma allora, se la luce è un'onda, rispetto a quale mezzo materiale si propagava? Questo era il problema.
Il concetto di etere
Molti tra i fisici più illustri affermarono che doveva esserci "qualcosa" che doveva avere certe particolari caratteristiche che chiamarono etere cosmico o "etere". L'etere permeava l'intero universo permettendo alla luce di andare ovunque. Secondo quel modello meccanico, l'etere doveva possedere proprietà insolite. In primo luogo doveva essere tenue e privo di viscosità apprezzabile, perché altrimenti non avrebbe potuto espandersi ovunque nell'universo. E non doveva offrire resistenza al moto dei corpi materiali, poiché per esempio i pianeti, nel moto di rivoluzione, avrebbero perso man mano energia fino a cadere nel Sole percorrendo traiettorie a spirale. Come se non bastasse, l'etere doveva essere molto rigido per trasportare un'onda all'elevatissima velocità della luce, infatti più un'onda si propaga velocemente e più necessita di un materiale pesante.
L'esistenza di onde elettromagnetiche che si propagano alla velocità c potrebbe essere vero soltanto in un sistema di riferimento fisso, poiché se ci muovessimo rispetto all'etere, per le trasformazioni di galileo, la velocità della luce dovrebbe essere diversa per ogni sistema di riferimento secondo la legge della composizione della velocità per la meccanica classica:
W= v + w
Dove w è la velocità del proprio sistema di riferimento rispetto al sistema di riferimento assoluto che è l'etere.
Esperimento Di Michelson Morley
 In
una serie di esperienze eseguite dal 1881 al 1887, i fisici statunitensi Michelson e Morley dichiararono l'inconsistenza fisica dell'etere.
In
una serie di esperienze eseguite dal 1881 al 1887, i fisici statunitensi Michelson e Morley dichiararono l'inconsistenza fisica dell'etere.
Essi tentarono di misurare la velocità della Terra rispetto ad esso,
infatti se l'ipotesi dell'etere era vera, allora questa sostanza doveva essere
ovunque e "farsi sentire", facendo per esempio in modo che quando
Lo strumento utilizzato dagli scienziati per l'esperimento, composto da una serie di specchi giustapposti in maniera tale da creare delle figure combinate di interferenza, non rilevò tuttavia alcun anomalia, in ogni direzione l'esperimento si facesse.
Questa conferma diede l'impulso decisivo ai fisici nell'abbandonare l'idea secolare dell'etere, aprendo però una voragine nella fisica che doveva ancora essere colmata.
I fisici della fine del XIX secolo fecero molti tentativi ingegnosi di risolvere il dilemma della luce e dell'etere, ma le loro spiegazioni o erano incompatibili con i dati sperimentali o erano prive di solide basi concettuali.
L'apparente incompatibilità fra la legge di propagazione della luce e il principio di relatività galileiana.
 Era di fondamentale importanza avere
una solida conferma sperimentale della reale velocità della luce. Questo valore
infatti trova luogo in molte delle leggi elettromagnetiche e confermare la velocità
prevista da Maxwell, era confermare l'esatta formulazione della teoria stessa. Molti
scienziati quindi si cimentarono nell'impresa, fino ad arrivare a Foucault, il quale riuscì ad approssimare meglio la velocità c. Essa è circa, c=300000 km/s.
Era di fondamentale importanza avere
una solida conferma sperimentale della reale velocità della luce. Questo valore
infatti trova luogo in molte delle leggi elettromagnetiche e confermare la velocità
prevista da Maxwell, era confermare l'esatta formulazione della teoria stessa. Molti
scienziati quindi si cimentarono nell'impresa, fino ad arrivare a Foucault, il quale riuscì ad approssimare meglio la velocità c. Essa è circa, c=300000 km/s.
 Dopo di lui, restava il problema
dell'universalità di questa legge. De
Sitter, matematico e astronomo olandese, facendo osservazioni sulle stelle doppie nel 1913, riuscì anche a dimostrare che la velocità della luce non
può dipendere dalla velocità del moto del corpo che emette la luce, infatti
considerando un sistema composto da due stelle, può succedere che nel loro moto
di rotazione una di esse si allontani da noi e l'altra si avvicini, che,
secondo il teorema già citato dell'addizione delle velocità, la velocità della
luce deve apparire differente, De Sitter mostrò però che le due velocità erano
identiche.
Dopo di lui, restava il problema
dell'universalità di questa legge. De
Sitter, matematico e astronomo olandese, facendo osservazioni sulle stelle doppie nel 1913, riuscì anche a dimostrare che la velocità della luce non
può dipendere dalla velocità del moto del corpo che emette la luce, infatti
considerando un sistema composto da due stelle, può succedere che nel loro moto
di rotazione una di esse si allontani da noi e l'altra si avvicini, che,
secondo il teorema già citato dell'addizione delle velocità, la velocità della
luce deve apparire differente, De Sitter mostrò però che le due velocità erano
identiche.

"Crollate le vecchie norme, non ancora sorte o bene stabilite le nuove..Nessuno più riesce a stabilirsi un punto di vista fermo e incrollabileAspettiamo che sorga finalmente qualcuno ad annunziarci il verbo nuovo."
Luigi Pirandello (La crisi di Fine secolo: la "relatività di ogni cosa")

1.2 Einstein e i due postulati della relatività
È opinione diffusa che la teoria della relatività sia nata per superare le difficoltà generati dall'esistenza dell'etere.
In realtà, le radici della relatività furono altre, e gli esperimenti volti a misurare l'etere svolsero un ruolo secondario nella sua nascita. Come ebbe infatti a ricordare lo stesso Einstein un anno prima di morire:
"l'esito dell'esperimento di Michelson non ebbe una grande influenza sull'evoluzione delle mie stesse idee[.]", si evince chiaramente che le motivazioni furono ben altre.
Tanto più che la memoria originale del 1905 è esplicita. Einstein enuncia sin dall'inizio quello che considera il problema da risolvere, cioè l'inconciliabilità delle equazioni di Maxwell dell'elettromagnetismo con le trasformazioni galileiane della meccanica.

Tuttavia, prima di argomentare con decisione i legami stretti della teoria della relatività con l'elettromagnetismo, si deve partire dal punto di partenza, cioè la risoluzione del problema della luce.
La risposta alla domanda "velocità c relativo a che cosa?" era ancora ignota, fino a quando nel 1905, all'età di 26 anni, un giovane impiegato all'ufficio brevetti di Berna, Albert Einstein propose una teoria rivoluzionaria nell'articolo Zur Elektrodynamik bewegter Körper (Sull'elettrodinamica dei corpi in movimento che risolveva il dilemma e al tempo stesso modificava le fondamenta proprie del pensiero fisico.
Einstein scriveva semplicemente che l'etere era un'ipotesi fittizia e la risposta di Einstein alla domanda: "rispetto a che cosa la luce si muove alla velocità c?" fu: "Rispetto a chiunque la osservi".
Egli riassunse i suoi nuovi concetti nella teoria della relatività ristretta (o speciale), ristretta in quanto valida soltanto nel caso di un sistema di riferimento in moto traslatorio rettilineo ed uniforme.
Egli cementò la sua nuova teoria su due postulati chiave:
 E'
necessario comunque ricordare che i postulati in fisica hanno un fondamento
sperimentale, infatti la loro validità non dipende solo, come nel caso dei
postulati matematici, dalla coerenza del sistema formale che ne deriva, ma
dall'accordo delle loro conseguenze empiriche con i dati. Ovvero, seguendo il
pensiero epistemologico dominante dell'epoca, il Neopositivismo, i postulati della fisica dovevano essere
verificabili sperimentalmente.
E'
necessario comunque ricordare che i postulati in fisica hanno un fondamento
sperimentale, infatti la loro validità non dipende solo, come nel caso dei
postulati matematici, dalla coerenza del sistema formale che ne deriva, ma
dall'accordo delle loro conseguenze empiriche con i dati. Ovvero, seguendo il
pensiero epistemologico dominante dell'epoca, il Neopositivismo, i postulati della fisica dovevano essere
verificabili sperimentalmente.
tutta la conoscenza rimane fallibile, congetturale..
..Noi impariamo attraverso confutazioni, cioè attraverso l''eliminazione di errori []. La scienza è fallibile perché la scienza è umana. »
Karl R. Popper, La società aperta e i suoi nemici, Vol. I, Platone totalitario, dalla IV di copertina.
Il 1° postulato decreta che nella relatività, le leggi della fisica sono uguali per tutti gli osservatori che si trovano in sistemi di riferimento inerziali.
L'argomento di inerziale in fisica è zona delicata, perché bisogna essere precisi e definire inerziale, quel sistema di riferimento che è in moto rettilineo ed uniforme nel tempo. In natura esistono luoghi approssimati a sistemi inerziali quasi perfetti come per esempio le stelle fisse visibili, le quali permangono in uno stato di quiete o di moto rettilineo ed uniforme l'una rispetto all'altra.
Questo enunciato si estende anche ai fenomeni elettromagnetici; esso include tutte le leggi della fisica e quindi va oltre il principio di relatività di Galileo-Newton che riguarda solo le leggi della meccanica classica.
Il 2° postulato stabilisce l'indipendenza della velocità della luce dallo stato di moto della sorgente che lo emette, cioè la si deve considerare come una costante universale, una specie di G gravitazionale.
Ed è proprio questo postulato il punto forte della relatività. Infatti come Einstein stesso scriveva:
«La teoria della relatività ristretta non è altro che un adeguamento del concetto di sistema inerziale alla convinzione, maturata con l'esperienza, che la velocità della luce sia costante rispetto ad ogni sistema inerziale». (Albert Einstein, Lettera a Michele Besso n◦ 22).
Dati questi postulati, la relatività spiega facilmente il risultato dell'esperienza di Michelson Morley, poiché qualunque sia la velocità della Terra rispetto a qualunque oggetto, un osservatore sulla Terra misurerà la stessa velocità della luce indipendentemente dalla posizione, esattamente ciò che i due fisici statunitensi scoprirono empiricamente.
Spazio e tempo nella Relatività
Se da una parte la relatività facilita la comprensione di alcuni dati sperimentali e ne risolve le problematiche, dall'altra, la relatività è una di quelle teorie che necessitano di una revisione totale dei fondamenti stessi della fisica.
Per intenderci, non si deve rimanere stupiti se si sente affermare che lo spazio e il tempo di come lo misuriamo noi non è altro che un caso particolare di infiniti altri spazi e tempi.
La difficoltà propria della teoria è il fatto che essa viola gran parte di quei casi o eventi che noi consideriamo come "senso comune", che basano la propria validità su principi logici evidenti che non necessitano dimostrazione, come il principio di identità e di non contraddizione. È affascinante poter scoprire come in un mondo dominato dal relativismo, l'unica verità necessariamente valida anche oggi rimane il principio di "causalità". Dovesse scomparire anche quello potremo essere in grado di affermare che il passato influenza il futuro e viceversa, fatto che si spera non possa mai accadere.
"Nessuna conclusione è certa: ogni asserto umano, quale che sia la sua struttura, è provvisorio e suscettibile di controversie. Relativismo? Certamente. Solo gli dei promulgano verità non negoziabili. Gli umani, invece, fabbricano teorie per meglio adattarsi al loro ambiente."
Enrico Bellone

Fig. 8 Dalì deforma gli orologi (lo strumento che misura il tempo per eccellenza) per invitare l'osservatore a considerare la dimensione temporale con occhio nuovo e, oltre a ciò, racchiude nello spazio onirico della tela delle vaghe forme, come se la nostra mente registrasse i nostri ricordi in modo non convenzionale, rivoluzionario, come il lo stesso Albert Einstein ci ha insegnato a fare.
Dilatazione dei tempi e contrazione delle lunghezze
 Per capire subito quali furono le
immediate implicazioni dei due postulati faccio un esempio.
Per capire subito quali furono le
immediate implicazioni dei due postulati faccio un esempio.
Questo è solo un assaggio della relatività, per quello che si può cercare di intuire, che ci racconta perché la costanza della luce, cioè il fatto che la luce si muove alla stessa velocità, incida sul passare del tempo.
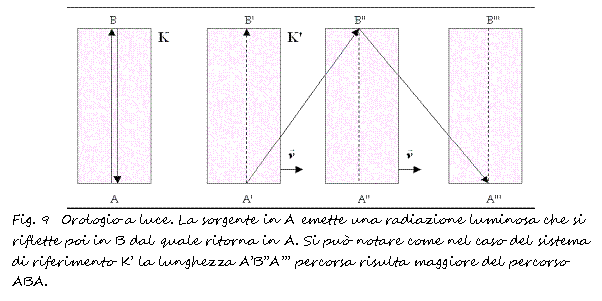
Einstein dimostrò illusorio il principio dell'assolutezza del tempo con il ragionamento dell'orologio a luce, intendendo quel dispositivo che calcola il tempo attraverso l'emissione di un fotone il quale emesso da una sorgente rimbalza fra due specchi piani e paralleli e quando torna indietro ferma l'orologio.
Quindi consideriamo questo orologio in cui un fotone che facciamo andare avanti ed indietro, rimbalza fra due specchi. Egli ha il suo rintocco ogni volta che il fotone rimbalza dallo specchio che è stato emesso.
Se facciamo muovere i due specchi di una certa velocità v possiamo notare che il fotone, per tornare al rintocco, dovrà fare un percorso più lungo ed è chiaro che se si muove alla stessa velocità, farà il rintocco più tardi.
Stessa considerazione si deve fare anche in relazione allo spazio, il quale non si modifica in rapporto alle leggi di Galileo, ma secondo le leggi formulate dalla teoria della relatività. Ogni lunghezza si contrae e questo fenomeno è tanto più evidente quanto la velocità aumenta.
La velocità della luce rimane infatti costante nel tempo e nello spazio e quindi sono il tempo e lo spazio stesso che si devono in qualche modo adattare.
E questo è un fatto che non è minimamente considerato dalla fisica classica che pensava al tempo come un'entità fisica invariante, e poneva le basi per uno spazio "assoluto", ma soprattutto questi cambiamenti relativistici trascendono del tutto il nostro senso comune.
E' questa la grande novità della relatività ristretta, in cui non sono le dimensioni spazio-temporali a rimanere costanti, ma le leggi della fisica, infatti il concetto forse più chiarificante ed importante della teoria, il concetto del sistema di riferimento, esplicita il fatto che si devono riconsiderare le dimensioni fisiche dello spazio e del tempo in funzione della velocità relativa di un sistema di riferimento rispetto ad un altro, tuttavia senza superare la velocità della luce.
Per esempio, se Io sono l'osservatore A del sistema di riferimento alfa, e B un altro osservatore posto in un altro sistema di riferimento beta, noteremo che analizzando un certo evento fisico, come il moto di un razzo o di un pianeta in un certo periodo nel tempo, i nostri calcoli saranno diversi, ma nessuno dei due dirà che i calcoli dell'altro siano giusti o meno, perché la relatività stessa impone che ogni sistema di riferimento inerziale ha una pari dignità scientifica rispetto a qualsiasi altro sistema inerziale, quindi entrambi i calcoli saranno "veri".
Un'ora, non è solo un'ora, è un vaso colmo di profumi, di suoni, di progetti, di climi
Marcel Proust, Alla ricerca del tempo perduto
Le trasformazioni di Lorentz
Sulla base del principio di costanza della velocità della luce è possibile determinare, dal puro e semplice punto di vista matematico, un insieme di nuove trasformazioni che collegano le osservazioni fatte da due osservatori solidali con due differenti sistemi inerziali. In questa sede non intendiamo dimostrare rigorosamente come si possa dedurre tali trasformazioni, ma ci limitiamo semplicemente ad enunciarle e a commentarle adeguatamente, mettendo bene in luce le conseguenze rivoluzionarie a cui portano. Le trasformazioni di coordinate tra due sistemi inerziali K e K , di cui il secondo trasli con velocità w lungo l'asse x del primo, sono le trasformazione di Lorentz dove c indica la velocità della luce.
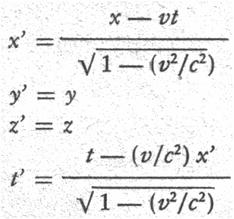

Soffermiamoci ora sulle trasformazioni e facciamo una prima importante osservazione:
Se consideriamo le coordinate y e z come ininfluenti per il moto, notiamo che la costante c è presente in tutte le formule dello spazio e del tempo; generalmente si può osservare come tutte le leggi della relatività implichino la costante c, al contrario della meccanica classica in cui le uniche costanti sono valide solo in certi sistemi di riferimento e per certe leggi. Un'altra osservazione riguarda la coordinata temporale t rispetto a K la quale dipende non solo dalla corrispondente coordinata temporale t rispetto a K, ma anche da quella spaziale x. Vi è quindi una già netta e chiara distinzione dalle trasformazioni di Galileo che considerava il tempo costante in tutti i sistemi inerziali (t = t , per qualsiasi valore di t e t ). Per questo motivo Lorentz usava dire che il tempo in K è locale, cioè dipende non solo dalla coordinata temporale in K, ma anche da quella spaziale. Il risultato matematico appena ottenuto appare, ad un'analisi superficiale, un paradosso, in quanto afferma che la simultaneità di due eventi non è un dato assoluto, come invece siamo ritenuti a credere in base al senso comune.
'quando seguo con gli
occhi sul quadrante di un orologio il movimento delle lancette non misuro una
durata, come pare si creda, mi limito a contare delle simultaneità, il che è
molto diverso'
Bergson
Verifiche sperimentali
La dilatazione dei tempi e la contrazione delle lunghezze non sono osservabili e percepibili dai nostri sensi, perché le velocità coinvolte nella nostra vita quotidiana sono molto inferiori a quella della luce. Tuttavia, la nuova teoria ha ricevuto numerose conferme sperimentali nell'ambito dello studio delle particelle elementari, in quanto esse possono viaggiare a velocità confrontabili con quelle della luce, in natura, per esempio i raggi cosmici, o per accelerazione indotta dall'uomo negli acceleratori di particelle.
La prima corroborazione storica della teoria della relatività in relazione alla dilatazione dei tempi, ha riguardato una delle più spettacolari conferme della relatività, cioè il tempo di vita medio dei muoni: si tratta di particelle subatomiche prodotte nell'alta atmosfera dallo scontro di particelle del vento solare con i nuclei degli atomi di gas rarefatti, e che decadono dopo un tempo τ, detto "vita media", il cui valore sperimentale è, per un muone in quiete,
τ0 = 2, 197 μs.
Osservando allora un fascio di muoni che viaggiano a velocità dell'ordine di quella della luce, secondo la teoria newtoniana la distanza percorsa nell'arco di tempo previsto dovrebbe essere data da
l0 = c · τ = 660m
e quindi il fascio dovrebbe sostanzialmente esaurirsi negli strati alti dell'atmosfera. Al contrario, si
riesce a rivelare un gran numero di muoni che riescono a raggiungere la bassa troposfera (il cui spessore è di circa dieci chilometri). Questo risulta spiegabile solo in termini relativistici, proprio come effetto della dilatazione dei tempi: se ad esempio la velocità dei muoni è
v = 0, 999 c si prevede che il fattore di dilatazione assuma il valore:
τ = 48, 334 μs
l = c · τ =
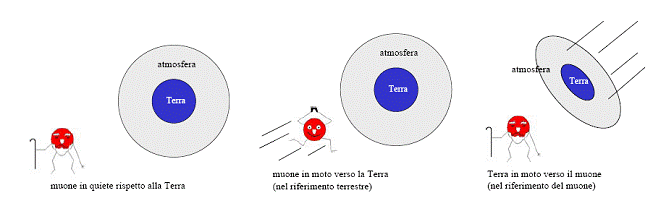
Fig. 11
a) Muone in quiete rispetto alla Terra: τ vita = 2.197 μs, ; l = 10km;
b) Muone in moto rispetto al riferimento terrestre: τ vita = 48.334 μs,; l = 10km;
c) Terra in moto rispetto al riferimento del muone: τ 0vita = 2.197 μs; l0 = 450m
 Come rappresentato simbolicamente in
figura, l'esempio del muone può anche
essere visto come una conferma della contrazione delle distanze. Se infatti
ci mettessimo nel riferimento solidale al muone, allora sarebbe
Come rappresentato simbolicamente in
figura, l'esempio del muone può anche
essere visto come una conferma della contrazione delle distanze. Se infatti
ci mettessimo nel riferimento solidale al muone, allora sarebbe
Δt =4503 · 108 = 1, 5 μs (59)
e quindi inferiore alla vita media del muone.
Cosa non è "relativo" e lo spazio di Minkowski
Nella relatività, le grandezze come lo spazio, il tempo e la massa non sono assolute, ma dipendono dal sistema di riferimento dell'osservatore. La velocità della luce c, però, rimane la stessa per tutti gli osservatori. Ne esistono altri di questi invarianti relativistici? Sì, e questi invarianti stanno alla base della descrizione oggettiva della realtà fisica nella teoria della relatività.
Un invariante è la carica elettrica. Sebbene la massa di un elettrone aumenti con la velocità la sua carica rimane invariata. Ma c'è un'altra quantità la quale rimane invariante. Questa è l'intervallo spaziotemporale, una sorta di distanza quadridimensionale, non tra due punti nello spazio ma tra due eventi nello spazio e nel tempo. Esso è dato da un'espressione che somiglia a un teorema di Pitagora modificato:
![]()
L'invarianza dell'intervallo spaziotemporale indica che dietro le sabbie mobili dello spazio e del tempo relativistici rimane qualcosa di assoluto. Questo assoluto è lo spazio-tempo o cronotopo, una "impalcatura" quadridimensionale che lega lo spazio ed il tempo. I punti dello spazio-tempo sono eventi, specificati da quattro coordinate.
Nelle trattazioni della relatività a livello più avanzato, conviene considerare vettori quadridimensionali detti quadrivettori e sebbene i valori dei singoli componenti dipendano dalla scelta del sistema di coordinate, la lunghezza del vettore no.
Altre quantità si possono combinare tra loro per costruire quadrivettori la cui lunghezza è invariante. Per esempio, l'energia e i tre componenti spaziali della quantità di moto si combinano per formare un singolo quadrivettore.
Ma il merito più grande va a Minkowski per l'aver dato una formulazione geometrica della relatività ristretta. Il matematico lituano insegnante di Einstein a Zurigo fu il primo ad intuire infatti come "il matrimonio fra lo spazio ed il tempo" fosse insito nei postulati della relatività.
In una conferenza tenuta a Colonia nel 1908, per illustrare alcuni concetti relativistici affermò fra l'altro:" .. Nessuno è mai stato in grado di osservare un dato luogo se non in un certo tempo, né osservare un tempo se non in un certo luogo."..
Fig.
12 Spazio di Minkowski, caratteristici sono i coni degli eventi, gli unici dove è possibile viaggiare nello
spazio-tempo

La massa e la quantità di moto nella relatività einsteiniana
 Se proviamo ad applicare le leggi
della relatività ristretta anche alla massa e alla quantità di moto, pietre angolari invarianti della meccanica newtoniana, poiché nei
sistemi di riferimento inerziali sono valide le trasformazioni di Lorentz,
differenti da quelle di Galileo, ne segue che anche le espressioni
relativistiche dell'energia e della quantità di moto che sono dentro questi
sistemi di riferimento, sono diverse dalle corrispondenti classiche. Necessitano
quindi di essere riviste. In particolare, Einstein, indagando sulle proprietà
della massa, scoprì un fatto impressionante. Attraverso una semplice
"esperienza mentale" (Gedankenxperiment, in tedesco) scoprì la nota relazione
che lega massa
Se proviamo ad applicare le leggi
della relatività ristretta anche alla massa e alla quantità di moto, pietre angolari invarianti della meccanica newtoniana, poiché nei
sistemi di riferimento inerziali sono valide le trasformazioni di Lorentz,
differenti da quelle di Galileo, ne segue che anche le espressioni
relativistiche dell'energia e della quantità di moto che sono dentro questi
sistemi di riferimento, sono diverse dalle corrispondenti classiche. Necessitano
quindi di essere riviste. In particolare, Einstein, indagando sulle proprietà
della massa, scoprì un fatto impressionante. Attraverso una semplice
"esperienza mentale" (Gedankenxperiment, in tedesco) scoprì la nota relazione
che lega massa
ed energia:
E=mc2
 Questo è un enunciato universale che ammette l'equivalenza e quindi la relativa trasformazione dall'una
all'altra di massa ed energia,
quindi si è scoperto un'invariante e cioè che: la massa-energia totale nell'universo si deve conservare.
Questo è un enunciato universale che ammette l'equivalenza e quindi la relativa trasformazione dall'una
all'altra di massa ed energia,
quindi si è scoperto un'invariante e cioè che: la massa-energia totale nell'universo si deve conservare.
Questa scoperta diede un impulso incredibile alla futura fisica nucleare, che basandosi proprio su questa legge, ora è in grado di indagare in maniera molto più approfondita nel mondo delle particelle, tramite i cosiddetti acceleratori di particelle.
 (La legge ha trovato immediata
applicazione, anche e soprattutto tramite i lavori di Enrico Fermi, padre della
fissione nucleare, il quale ne confermò la veridicità. Nei processi della
fissione o ancora meglio della fusione, possiamo fare esperienza come
trasformando la massa in energia, si è in grado di ricavare, da un pezzettino
minuscolo di massa, una grandissima energia.)
(La legge ha trovato immediata
applicazione, anche e soprattutto tramite i lavori di Enrico Fermi, padre della
fissione nucleare, il quale ne confermò la veridicità. Nei processi della
fissione o ancora meglio della fusione, possiamo fare esperienza come
trasformando la massa in energia, si è in grado di ricavare, da un pezzettino
minuscolo di massa, una grandissima energia.)
Fig. 13 Enrico Fermi, Nobel
per la fisica
Relatività ristretta tra di noi
Tutte le nuove scoperte sono sintetizzabili tramite le formule relativistiche, in cui si può notare che in ciascuna di esse è sempre presente il coefficiente della velocità della luce.
Ma perché noi non ci rendiamo conto di tali effetti neanche minimamente? La spiegazione sta nel fatto che normalmente noi viaggiamo a velocità non relativistiche e questo rende molto arduo la rivelazione empirica della relatività. Tuttavia è possibile ,tramite esperimenti di particelle che implicano velocità prossime a quelle della luce, notare che i tempi realmente si dilatano, mentre lo spazio si restringe. Senza tali effetti molte particelle nella natura non vivrebbero abbastanza a lungo per essere identificate dai nostri rivelatori, come quelle particelle radioattive che decadono molto rapidamente emettendo grandi quantità di energia, Risonanza.
Dieci anni dopo la teoria della relatività ristretta, comunque verrà pubblicata una teoria ancora più estesa e completa, la teoria della relatività generale con una matematica molto più difficile, alla quale hanno partecipato indirettamente anche molti matematici tra i quali anche l'italiano dell'800, Ricci Corpastro.

Fig. 14 Una raffigurazione moderna del concetto del tempo.
 |
| Appunti su: |
|
| Appunti Biologia |  |
| Tesine Chimica |  |
| Lezioni Geografia |  |