 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1734 | Gradito: |
Leggi anche appunti:Relativita'RELATIVITA' La teoria della relatività di Einstein unifica i due tradizionali Cenni di relatività generaleCenni di relatività generale Anche la relatività generale ha un ruolo fondamentale Teoria della relativitàTeoria della relatività La teoria della relatività fu formulata all'inizio del |
 |
 |
Relatività
Albert Einstein: cenni biografici.
Albert Einstein, nato nel 1875 ad Ulm, piccola ma famosa cittadina tedesca, è morto nel 1955 a Princeton nel New Jersey. Trascorse la sua prima giovinezza a Monaco educato nel rigido sistema scolastico bavarese; dopo un breve soggiorno a Milano si trasferì a Zurigo dove continuò gli studi fino al dottorato di matematica e fisica presso il Politecnico. Dopo la laurea continuò a dedicarsi intensamente ad alcuni problemi di fisica teorica anche quando, per risolvere i più gravi ed immediati problemi economici, prese la cittadinanza svizzera per assumere un modesto impiego presso l'Ufficio Brevetti di Berna. Nel 1905 pubblicò tre articoli sugli Annalen der Phisik, il primo sui quanti di luce, il secondo sul moto browniano, destinato a confermare l'atomicità della materia, il terzo sui fondamenti della relatività ristretta. Questi ormai storici lavori furono l'avvio di una lunga e brillante carriera accademica, iniziata a Zurigo e proseguita in terra tedesca fino al 1932 quando, a causa delle persecuzioni antisemitiche naziste, fu costretto ad abbandonare la Germania per essere accolto a braccia aperte negli U.S.A.. Einstein, naturalizzato cittadino americano, si stabilì a Princeton, dove insegnò presso l'Institute for Advanced Studies fino al 1945, anno del suo ritiro dall'attività accademica.
Nella storia del potere creativo del pensiero umano, Einstein rappresenta un simbolo, un personaggio che ha colpito la fantasia della gente, uno scienziato che ha dato un alto e qualificato contributo allo sviluppo della fisica moderna. Quest'uomo considerato da molti artista e quasi profeta che disprezzava la violenza e la guerra fu, suo malgrado, doppiamente coinvolto nella realizzazione della bomba atomica di cui è considerato padre putativo: in primo luogo perché uno dei risultati della teoria della relatività, riguardante la cosiddetta equivalenza massa - energia (E=mc2), doveva rappresentare il punto di partenza del successivo sviluppo dell'energia nucleare; in secondo luogo perché si deve al suo intervento (voluto da altri) se il governo degli U.S.A. mise a disposizione i capitali che portarono alla costruzione della bomba di Hiroshima. Tornando alle ricerche teoriche di Einstein, dobbiamo ricordare 'I fondamenti della teoria della relatività generale' (1916) frutto di oltre dieci anni di studio. Fino agli ultimi anni della sua vita egli tentò più volto di elaborare una teoria capace di unificare su una comune base geometrica i fondamentali campi allora meglio conosciuti: il capo gravitazionale e il campo elettromagnetico. Nonostante lo sforzo di elaborazione tecnica, i risultati non furono quelli sperati. 'La natura non si lasciò convincere a fare ciò che forse non è nella sua stessa natura'. Dopo la seconda guerra mondiale, Einstein cercò in tutti i modi di favorire la pace nel mondo, promuovendo una vasta campagna popolare contro la guerra e le persecuzioni razziste. Proprio una settimana prima di morire, insieme ad altri sette Nobel, compilò una dichiarazione pacifista contro le armi nucleari. Questo messaggio all'umanità, che rappresenta una specie di testamento spirituale dello scienziato, termina con queste parole:
'Noi rivolgiamo un appello come esseri umani a esseri umani: ricordate la vostra umanità e dimenticate il resto. Se sarete capaci di farlo è aperta la via di un nuovo paradiso, altrimenti è davanti a voi il rischio della morte universale'.
La relatività
Nel 1919 Einstein scrisse per il 'London Times' un articolo ('Che cos'è la teoria della relatività?') in cui spiegava ad un pubblico di non specialisti la sua celebre teoria.
«.la teoria della relatività»- afferma Einstein-«assomiglia ad un edificio a due piani separati: la teoria speciale e la teoria generale.
La teoria speciale [.] si applica a tutti i fenomeni fisici tranne la gravitazione. La teoria generale conduce alla legge della gravitazione e alle relazioni di essa con altre forze della natura.»
La teoria della relatività speciale o ristretta fu formalizzata per la prima volta attraverso un saggio pubblicato nel 1905. Successivamente, nel 1916, il fisico propose una nuova teoria (la teoria della relatività generale) che superava la precedente, includendola come caso limite. Tre anni dopo, nel 1919, questa teoria ebbe, ad opera di Eddington, una clamorosa conferma sperimentale.
Relatività ristretta
La relatività ristretta di Einstein si basa essenzialmente su due postulati che possono essere enunciati come segue:
Il moto assoluto uniforme non può essere rivelato;
La velocità della luce è indipendente dal moto della sorgente.
Sostanzialmente il primo postulato era già noto dal XVII secolo ed era stato formalizzato come principio di Newton: nella relatività Einstaniana, però, questo principio viene esteso non solo ai fenomeni meccanici ma include tutti i tipi di misure fisiche.
Ognuno dei due postulati sembrerebbe ragionevole: eppure dai due postulati presi insieme derivano alcune implicazioni che contraddicono il senso comune, cioè il nostro modo intuitivo di concepire la realtà. Una conseguenza immediata di questi postulati è che:
ogni osservatore misura lo stesso valore per la velocità della luce, indipendentemente dal moto relativo della sorgente e dell'osservatore
Facciamo un esempio per capire meglio quest'ultima affermazione. Consideriamo una sorgente luminosa S e due osservatori O1 e O2 uno fermo e l'altro in movimento verso S con velocità V
v O1
W
![]()
O2
S
(Figura A)
v
![]()
![]()
V O1
W O2
S
(Figura B)
dove vediamo O2 fermo, mentre S e O1 si muovono verso destra con velocità V (il moto assoluto non può essere rivelato quindi non possiamo sapere se è O2 in movimento verso S come nella figura
A oppure se S e O1 si muovono verso destra con velocità V come nella figura B).Per il secondo postulato O2 vede che la velocità della luce è uguale a c visto che questa è indipendente dal moto della sorgente. Da questo esempio si può capire come le nostre idee intuitive sulla composizione delle velocità non valgono più se si considerano velocità prossime a c.
Dilatazione dei tempi e contrazione delle lunghezze.
Einstein riuscì a dimostrare che le ampiezze degli intervalli di tempo e di spazio tra due eventi dipendono dal sistema di riferimento nel quale si osservano gli eventi.
Prendiamo ora in esame il problema della dilatazione dei tempi.

Consideriamo un sistema S1
formato da una sorgente luminosa A e da uno specchio posto ad una distanza D
dalla sorgente (fig.C)
Si consideri un raggio luminoso (velocità c) che esce dalla sorgente A vi ritorni dopo essere stato riflesso dallo specchio. Lo spazio percorso dal raggio luminoso è uguale a 2D e il tempo impiegato è: <t1 = 2D/c.
Consideriamo ora il sistema S1 (specchio-sorgente) in movimento rispetto ad un sistema S immobile (fig.D)
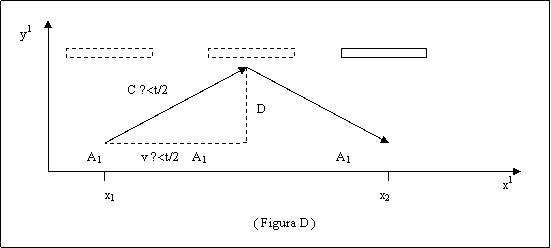
Come si può notare il raggio luminoso, visto dal sistema S, compie un tragitto più lungo rispetto a quello compiuto in S1. Calcoliamo lo spazio percorso dal raggio per arrivare allo specchio rispetto ad S. Ipotizzando la velocità di S1 uguale a v e il tempo impiegato per andare da x1 a x2 uguale a <t, questo spazio è uguale a c∙<t/2 e risulta formato da due componenti (fig.D). Applicando il teorema di Pitagora si ha:
(c∙<t/2)2 = D2 + (v∙<t/2) 2
[c2∙(<t) 2]/4 - [v2∙(<t) 2]/4 = D2
<t) 2 ∙ (c2 - v2) = 4D2
<t = 2D / (c2 - v2)
<t = (2D/c) ∙ (1 - v2/c2)
Avendo posto <t1 = 2D/c si ha:
<t = <t 1/ (1 - v2/c2) = c <t1 dove c (1 - v2/c2)
Dunque il tempo misurato in S risulta essere dilatato di un fattore c, il quale aumenta se si considerano velocità prossime a quella della luce.
Strettamente connesso alla dilatazione dei tempi è il fenomeno della contrazione della lunghezza.

Immaginiamo un regolo di lunghezza L0
= x2 - x1 visto da un osservatore in movimento con
velocità v (fig.E)
Se O1 impiega un tempo <t per passare da un'estremità all'altra del regolo allora la lunghezza del regolo sarà L0 = x2 - x1 = v ∙ <t.
Consideriamo ora il caso in cui l'osservatore sia fermo e il regolo si muova di moto relativo (fig.F)

Il regolo impiegherà, per passare davanti all'osservatore, un tempo <t1 minore di <t secondo un fattore c (1 - v2/c2).
Se il tempo è minore anche la lunghezza del regolo sarà tale:
L1 = v ∙ <t1 = v ∙ <t / c = L 0/ c = L0 (1 - v2/c2)
Una prova della dilatazione dei tempi: il decadimento dei muoni.
I muoni, o mesoni l, sono particelle create dal decadimento dei pioni (mesoni o) e si creano nell'alta atmosfera a migliaia di Km sul livello del mare. I muoni decadono seguendo la legge statistica della radioattività:
N(t) = N0 ∙ e-t/t
Dove N0 è il numero dei muoni all'istante t = 0, N(t) è il numero dei muoni all'istante t e t (tau) è la vita media di un muone (per i muoni fermi vale circa 2 ls).Supponiamo di rivelare 108 muoni ad un'altezza di 9000 Km. Sapendo che un muone tipico si muove alla velocità di 0.998 c, il tempo impiegato dalle particelle per arrivare al livello del mare è (5000 m)/0.998 c ls cioè 15 volte il valore della vita media. Ponendo N0 = 108 e t = 15t si ottiene: N = 108 ∙ e-15 = 30.6.
Dovremmo quindi aspettarci di rivelare circa 31 muoni al livello del mare. Invece, da esperimenti pratici, è risultato che il numero dei muoni rilevati è notevolmente maggiore. Questo perché la vita di un muone, misurata nel sistema di riferimento della terra aumenta del fattore 1/ (1 - v2/c2) che (per v = 0.998 c) vale, c= 15. Perciò per t ls si ha:
N = 108 ∙ e-1 = 3.68 ∙ 107
Questo dimostra che gli esperimenti pratici concordano con la teoria relativistica.
Sincronizzazione degli orologi e simultaneità.
Da una prima analisi dei postulati della relatività risulta evidente come la teoria Einstaniana contraddica spesso il 'senso comune'. Accettando la relatività, i concetti di spazio e di tempo dettati dalla fisica classica cambiano enormemente e bisogna quindi abbandonare la convinzione che certe relazioni siano assolute. In particolare ora voglio dimostrare che il concetto di simultaneità non ha più valore assoluto e che:
due orologi sincronizzati in un sistema di riferimento non sono sincronizzati in qualsiasi altro sistema che si muova rispetto al primo
e che quindi:
due eventi che sono simultanei in un sistema di riferimento non lo sono in un altro che si muova rispetto al primo
Supponiamo di avere nel sistema S due orologi nei punti A e B distanti tra loro di una lunghezza L. Se un osservatore in A guarda l'orologio in B e regola il proprio orologio in modo che segnino entrambi lo stesso tempo, gli orologi non saranno sincronizzati a causa del tempo che la luce impiega per andare da A a B. Per una corretta sincronizzazione è necessario che l'osservatore in A calcoli il tempo di ritardo. Se in A e in B si verificano eventi simultanei tutti gli osservatori in S vedranno arrivare i segnali luminosi (emessi dagli eventi) prima da A o da B a seconda della loro posizione. Solo gli osservatori posti a metà strada tra A e B vedranno i segnali luminosi contemporaneamente. Si possono definire quindi simultanei due eventi in un sistema di riferimento se i segnali luminosi emessi dagli eventi stessi raggiungono nello stesso istante l'osservatore a metà strada tra gli eventi.

Per dimostrare che due eventi che sono
simultanei in un sistema S non lo sono in un sistema SI usiamo un
esempio introdotto da Einstein: consideriamo un treno che si muova con velocità
v rispetto ad un marciapiede fermo nel sistema S; il treno è fermo nel sistema
SI (ovviamente il sistema SI è in moto relativo rispetto
ad S). Sia CI un punto a metà strada tra le estremità del treno come
mostrato nella figura G:
Immaginiamo che le estremità del treno vengano colpite da due fulmini e che gli eventi si verifichino contemporaneamente (cioè C vede arrivare insieme i segnali luminosi emessi dai fulmini) nel sistema S. Gli eventi non potranno mai essere simultanei in SI in quanto un osservatore in CI si muove incontro ad A provocando così un ritardo del segnale proveniente da B.
Da questo risultato si può dedurre che se due orologi sono sincronizzati nel sistema di riferimento in cui sono fermi, essi non saranno sincronizzati in un altro sistema.
Massa relativistica e quantità di moto relativistica.
Le scoperte di Einstein misero in crisi non solo le concezioni della cinematica classica ma anche quelle della dinamica: in particolare venne dimostrato il fatto che l'equazione per la quantità di moto di un corpo (p=mv dove p è la quantità di moto, m la massa e v la velocità) è solo un'approssimazione che vale per corpi che si muovono a velocità insignificanti rispetto a quella della luce. Mi limiterò a spiegare intuitivamente i risultati di questa dimostrazione senza entrare nel dettaglio usando calcoli complicati.
Secondo la seconda legge della dinamica di Newton, se su un corpo agisce una forza F, questa subirà un'accelerazione direttamente proporzionale alla forza; in termini matematici la seconda legge è espressa così F=ma dove m è la massa del corpo, costante di proporzionalità diretta tra F e a.
Ora, se si considera un corpo che si muova con velocità v, esso sarà sottoposto al fenomeno della dilatazione dei tempi (cioè un osservatore fermo misurerà tempi più lunghi rispetto a quelli misurati dal corpo in movimento) e l'accelerazione, cioè la velocità in rapporto al tempo (a = v / t), diminuirà di conseguenza.
Quindi dobbiamo supporre che se un corpo si muove ad una certa velocità, mentre la sua accelerazione diminuisce, la sua massa aumenta: se non fosse così la seconda legge di Newton (F=ma) perderebbe di significato.
Possiamo quindi affermare che anche la massa non è più una proprietà assoluta di un corpo ma varia a seconda delle circostanze: dobbiamo quindi parlare di massa relativistica, che, secondo le leggi della relatività, è legata alla massa d'inerzia (la massa di un corpo in quiete) tramite la seguente relazione m0 = c ∙ m dove m0 è la massa relativistica e m la massa d'inerzia e c (1- v2 / c2 ). Di conseguenza anche l'equazione per la quantità di moto cambierà:
p = m0v = c mv
Energia relativistica.
Nella meccanica classica il lavoro compiuto dalla forza risultante che agisce su una particella è uguale alla variazione dell'energia cinetica della particella. Invece nella meccanica relativistica la forza risultante che agisce su una particella viene definita come la rapidità di variazione della quantità di moto relativistica. Einstein calcolò l'energia cinetica di una particella che si muove con velocità v uguagliando il lavoro compiuto dalla forza risultante alla variazione dell'energia cinetica; di questo calcolo (assai complicato) fornisco il risultato omettendo la dimostrazione:
Ec = cmc2 - mc2
Dove Ec è l'energia cinetica della particella che si muove con velocità v e c, come al solito è dato da c (1 - v2/c2).
Nell'espressione per l'energia cinetica è presente un termine indipendente dalla velocità della particella: si tratta di mc2. Questa grandezza è chiamata energia di riposo della particella.
L'energia totale E, allora, è definita come la somma dell'energia di quiete e dell'energia cinetica
E = Ec + mc2 = cmc2
Se v è molto minore di c possiamo approssimare il fattore utilizzando la serie binomiale (1 + x) n 1 + nx (con x << 1):
c = (1 - v2/c2) -1/2 1 + (1/2) ∙ (v2/c2)
Con questo risultato per l'energia cinetica relativistica si ottiene:
Ec = mc2(c mc2[1 + (1/2) ∙ (v2/c2) - 1] = (1/2) ∙ mv2
Si è così dimostrato che per velocità irrilevanti rispetto a c, l'energia cinetica relativistica ha praticamente lo stesso valore dell'energia cinetica secondo le teorie classiche della fisica. Spesso, nelle applicazioni pratiche, si conosce la quantità di moto di una particella o l'energia, piuttosto che la sua velocità. Combinando le equazioni dell'energia relativistica totale (E = c mc2 ) e della quantità di moto relativistica (p = c mv), possiamo ricavare l'equazione dell'energia in funzione della quantità di moto:
E = c mc2 t E2 = c (mc2) 2 t E2 = (mc) 2 / (1 - v2/c2)
Ricaviamo ora il termine v2/c2 dall'equazione per la quantità di moto relativistica
p = c mv t c = p/mv t c = p2 / m2v2 t 1 - v2/c2 = m2v2 / p2
1/c2 = v2/c4 + (v2/c2)(m2/p2) t 1/c2 = (v2/c2)(1/c2 + m2/p2)
1/c2 = (v2/c2)[(p2 + m2c2)/(p2c2)] t v2/c2 = (1/c2)[(p2c2)/(p2 + m2c2)
v2/c2 = p2/(p2 + m2c2)
Si ha dunque :
E2 = [1 - p2/(p2 + m2c2)] -1 ∙ (mc2) 2
E2 = [(p2 + m2c2 - p2)/(p2 + m2c2)] -1 ∙ (m2c4) t E2 = [(m2c2 + p2)/m2c2](m2c4)
E2 = m2c4+ p2c2 = p2c2 + (mc2) 2
Se l'energia di riposo (o di quiete) di una particella è trascurabile rispetto all'energia totale possiamo operare la seguente approssimazione:
E pc per E >> mc2
Quest'ultima è una relazione esatta tra energia e quantità di moto per le particelle che non hanno massa di riposo, come i fotoni.
Cenni sulla relatività generale.
Da un punto di vista matematico, la relatività generale è molto più complicata di quella ristretta: per questo ne fornirò solo una breve trattazione qualitativa.
La base della teoria generale della relatività è il principio di equivalenza:
un campo gravitazionale omogeneo è del tutto equivalente a un sistema di riferimento uniformemente accelerato
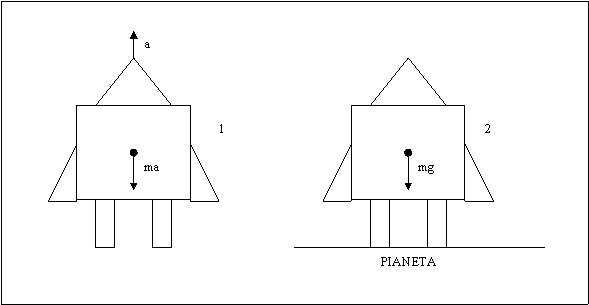
Ecco un esempio che chiarisce il
principio di equivalenza:
Se un'astronave, in assenza di campo gravitazionale, si muove con accelerazione a, un corpo al suo interno sarà sottoposto ad una forza F = m ∙ a nel verso opposto a quello del moto (figura 1).
Su un corpo all'interno dell'astronave ferma su un pianeta, agirà una forza pari a F=m∙g. Se poniamo g = -a le due forze (F=ma e F=mg) saranno uguali. Dunque si può concludere che non esiste alcun esperimento che possa distinguere un moto uniformemente accelerato dalla presenza di un campo gravitazionale.
Uno degli aspetti più interessanti della relatività generale è la nuova concezione di 'spazio curvo'. Secondo la teoria Einsteniana la materia, mediante il campo gravitazionale, agisce sullo spazio circostante alterandolo.
La relatività non si serve quindi della geometria euclidea, applicabile solamente ad uno spazio piatto. Ma che differenza c'è tra spazio curvo e spazio piatto ?
La seguente immagine dovrebbe fornire qualche chiarimento in più :

A sinistra, un cilindro è una superficie con curvatura nulla. Su di esso le linee geodetiche (si definisce geodetica l'ente più breve che unisce due punti) sono parallele, la somma degli angoli interni di un triangolo è di 180° e una sua porzione può essere distesa su un piano senza rotture. Al centro, una sfera è una superficie con curvatura positiva. Le linee geodetiche convergono fino ad avere un punto in comune, la somma degli angoli interni di un triangolo è maggiore di 180° e una sua porzione non può essere distesa su un piano, a meno di non dividerla in spicchi molto sottili. A destra, una sella è un esempio di spazio con curvatura negativa. Qui le linee geodetiche divergono, la somma degli angoli interni di un triangolo è minore di 180° e una sua porzione non può essere distesa su un piano a meno di non sovrapporre alcune sue parti. La luce ha la proprietà fisica di percorrere geodetiche dello spazio: per esempio un raggio di luce che ad un osservatore sulla Terra appare come una traiettoria rettilinea, in realtà percorre archi di circonferenza. La luce fa dunque capire che tipo di geometria segue lo spazio.
Nel 1915 le ipotesi di Einstein sul campo gravitazionale ebbero una clamorosa conferma: in quell'anno, infatti, si osservò la deflessione di un raggio di luce dovuta al campo gravitazionale solare. Tale osservazione fu resa possibile da un'eclissi solare e portò immediatamente fama internazionale a Einstein.


Un altro aspetto della relatività generale riguarda la variazione degli intervalli di tempo e quindi delle frequenze della luce in un campo gravitazionale. L'energia potenziale gravitazionale tra due masse M e m, distanti tra loro r è:
U = - GMm / r
dove G è la costante di gravitazione universale e si è posta l'energia potenziale uguale a zero quando la distanza tra le masse è infinita. L'energia potenziale riferita all'unità di massa in prossimità di una massa M è chiamata potenziale gravitazionale
= -GM / r
Secondo la teoria generale della relatività, gli orologi sono più lenti nelle regioni di basso potenziale gravitazionale (dunque in prossimità della massa). Se <t1 è un intervallo di tempo misurato da un orologio dove il potenziale gravitazionale è e <t2 è lo stesso intervallo misurato da un orologio dove il potenziale gravitazionale è la relatività generale prevede che la variazione relativa tra questi tempi sia all'incirca:
<t2 - <t1) / <t = ( ) / c2
(Visto che di solito questa variazione è molto piccola non importa per quale intervallo si divida il primo membro dell'equazione). Poiché un atomo che vibra può essere considerato come un orologio, la frequenza di vibrazione in una regione di basso potenziale, come ad esempio in prossimità del Sole, sarà minore di quella dello stesso atomo sulla Terra. Questo spostamento verso frequenze più basse e quindi lunghezze d'onda maggiori, è chiamato spostamento gravitazionale verso il rosso (gravitational red shift).
Altro fenomeno che rientra nelle previsioni della relatività è quello dei buchi neri, previsti per la prima volta da Oppenheimer e Snyder nel 1939. Secondo la teoria generale della relatività, se la densità di un corpo, come una stella, è abbastanza grande, l'attrazione gravitazionale sarà così grande che, una volta all'interno di un certo raggio critico, nulla potrà sfuggire, neanche la luce e le altre radiazioni elettromagnetiche. Nella meccanica Newtoniana, la velocità necessaria perché una particella sfugga dal campo gravitazionale di un pianeta o di una stella si trova imponendo che l'energia cinetica mv2 / 2 sia uguale all'energia potenziale GMm / r. La velocità di fuga che si ottiene :
mvf2 / 2 = GMm / 2 t vf2 = 2GM / r t vf = (2GM / r)
Se uguagliamo la velocità di fuga alla velocità della luce e risolviamo rispetto al raggio, otteniamo il raggio critico Rc , chiamato raggio di Schwarzschild :
vf = c c= (2GM / Rc ) t c2 = 2GM / Rc t Rc = 2GM / c2
Perché un corpo di massa uguale a quello del nostro Sole (1.99 ∙ 1030 Kg) sia un buco nero, il suo raggio deve essere circa 3 Km. Visto che un buco nero non emette alcuna radiazione e ci si aspetta che il suo raggio sia piccolo, la rivelazione di tale corpo non è facile e per individuarne uno l'unica possibilità è quella di studiare i suoi effetti sullo spazio circostante ad esso.
 |
| Appunti su: |
|
| Appunti Biologia |  |
| Tesine Geografia |  |
| Lezioni Chimica |  |