Relatività, Meccanica quantistica e crisi della Fisica Classica

Relatività, Meccanica quantistica e crisi della Fisica Classica

Fino agli ultimi anni del XIX secolo la comunità scientifica internazionale era convinta di possedere ormai saldamente tutte le leggi fondamentali della fisica: la meccanica di Newton e Galileo sembrava in grado di dare una spiegazione esauriente di tutti i fenomeni meccanici qualsiasi fosse la dimensione e la velocità dei corpi presi in esame, dagli oggetti della vita quotidiana fino ai costituenti ultimi della materia, passando per stelle e galassie; si riteneva, inoltre, che le equazioni di Maxwell potessero descrivere perfettamente tutti i fenomeni elettrici e magnetici. D'altra parte erano molto radicati i concetti di "causalità", di "determinismo" e di "meccanicismo": i fisici erano infatti convinti che conoscendo i parametri iniziali di un sistema (per esempio energia, quantità di moto e posizione dei suoi componenti) si potesse prevedere in modo assolutamente preciso l'evoluzione del sistema stesso, teoricamente anche dell'intero Universo; l'unico eventuale limite era costituito dagli inevitabili errori di misura, che con il tempo si sperava di ridurre il più possibile. Entità come "spazio" e "tempo" e l'idea di "simultaneità" erano ritenuti "assoluti", "eterni" e "indipendenti" da ogni tipo di fenomeno fisico: si riteneva cioè che la misura di un intervallo di tempo o di una lunghezza dovesse essere la stessa a prescindere dallo stato di moto dell'osservatore. Si può dire che la fisica classica era, in qualche modo, in pieno accordo con il "senso comune" dell'uomo, cioè con le idee e le aspettative che chiunque, anche un estraneo dal mondo della scienza, aveva ben fissate nel proprio immaginario. Tuttavia, a partire dai primi del '900, questi "pilastri" della fisica furono clamorosamente smentiti tra l'incredulità e, in alcuni casi, lo sconforto degli stessi autori delle nuove scoperte. Le due nuove teorie fondamentali che presero piede furono la Relatività (ristretta e generale) e la Meccanica Quantistica; a questi due nuovi sistemi sono indissolubilmente legati i nomi di personaggi illustri come Einstein, Planck, Heisenberg, Schrodinger, Bohr e molti altri ancora.

La Relatività Ristretta

La Teoria della Relatività Ristretta fu pubblicata da Albert Einstein nel 1905: l'argomento principale di cui si tratta è il comportamento di oggetti ed eventi osservati in sistemi di riferimento inerziali, in particolare quando vengono raggiunte velocità vicine a quella della luce (c=3*10^8 m/s). Fu proprio la luce a far nascere il dibattito in quegli anni; nelle equazioni di Maxwell il valore della sua velocità appariva come una costante: nacque il problema di determinare in quale sistema di riferimento la luce avesse quella velocità. Convinti che le radiazioni elettromagnetiche, così come le onde meccaniche, si potessero propagare solo in un mezzo, fu ipotizzata la presenza di un fluido, detto "etere", immobile nell'universo e quindi da considerare come sistema inerziale principale. Gli scienziati Michelson e Morley misurarono con un interferometro la velocità della luce sulla terra, la quale, teoricamente, si muoveva con velocità v=30 km/s rispetto all'etere. Ci si aspettava di trovare il valore c+v o c-v, ma i due fisici trovarono proprio il valore c, in contrasto con la composizione galileiana delle velocità. Einstein allora introdusse due postulati che eliminarono ogni contraddizione:

Principio di relatività: le leggi della fisica sono le stesse in tutti i sistemi di riferimento inerziali.

Costanza della velocità della luce: la velocità della luce nel vuoto è c=3*10^8 m/s in tutti i sistemi di riferimento inerziali.

Il primo postulato è simile al principio di relatività di Galileo-Newton, ma si estende anche ai fenomeni elettromagnetici e non solo a quelli meccanici. Se il secondo postulato fosse falso, inoltre, si potrebbe trovare un sistema di riferimento principale (in contraddizione col primo postulato), cosa che Michelson e Morley hanno cercato inutilmente di fare. Einstein riprese i risultati di un altro scienziato, Lorentz, e introdusse nuove "trasformazioni", ovvero relazioni che consentono di passare dalle coordinate spazio-temporali di un sistema di riferimento inerziale a quelle di un altro sistema, anch'esso inerziale. Se il sistema S' si muove di moto rettilineo uniforme rispetto a S lungo la direzione x con velocità v, e per t=t'=0 S e S' coincidono, le coordinate spazio-temporali sono legate dalle relazioni:

x-vt t-(vx/c^2)

x'= ____________ y'=y z'=z t'= _____________

√(1-v^2/c^2) √(1-v^2/c^2)

Bisogna notare come, per v molto piccole, tali trasformazioni siano simili a quelle classiche: Galileo e Newton, quindi, avevano ragione, ma solo in relazione a piccole velocità, mentre per alte velocità bisogna utilizzare un altro modello. Una prima paradossale conseguenza della relatività ristretta è la crisi dell'idea di simultaneità. Due eventi sono simultanei se un osservatore vede, orologio alla mano, che tali eventi accadono contemporaneamente. Se però l'osservatore non è equidistante dagli eventi, poiché la velocità della luce è finita, egli vede l'evento più lontano in ritardo rispetto al primo. Per esempio, se vediamo con un telescopio un'esplosione di una supernova, dobbiamo considerare che quell'evento è accaduto in realtà qualche miliardo di anni fa, perché la luce ha impiegato del tempo per raggiungere l'obbiettivo del telescopio. Si consideri ora un vagone ferroviario che viaggia con velocità costante v. Se un osservatore sul treno si posiziona sul punto medio del vagone e manda due fasci di luce verso gli estremi della carrozza, egli vedrà i fasci raggiungere contemporaneamente le due pareti. Un osservatore sulla terra, invece, poiché c non cambia, vedrà toccare prima il fascio che si oppone al moto del treno e dopo quell'altro fascio: questo perché la coda del vagone si avvicina alla luce mentre la testa se ne allontana. Si può concludere che termini come "prima", "dopo" e "contemporaneamente" sono concetti relativi in quanto dipendono dall'osservatore, e non sono valori assoluti. La relatività ristretta mina alla base anche l'idea di spazio e tempo assoluti: a velocità "relativistiche", infatti, i corpi e le distanze subiscono una contrazione lungo la direzione del moto, mentre gli intervalli di tempo risultano essere "dilatati", cioè più lunghi rispetto a quanto non siano a basse velocità. Se ∆t è l'intervallo di tempo tra due eventi misurato da un osservatore in quiete rispetto ad essi, e ∆t' è l'intervallo misurato da un altro osservatore in moto con velocità v rispetto a tali eventi, tra i due intervalli sussiste la relazione:

∆t

∆t'= ____________

√(1-v^2/c^2)

Analogamente, se l è la distanza fra due punti misurata da un osservatore in quiete rispetto ad essi, e l' è la distanza misurata da un altro osservatore in moto con velocità v rispetto ai punti stessi, tra le due misure sussiste la relazione:

l'= l*√(1-v^2/c^2)

Si può notare come per velocità elevate tempo e lunghezza subiscano modifiche consistenti, mentre a velocità "quotidiane" le variazioni sono del tutto trascurabili. Per quanto riguarda la composizione delle velocità, se un sistema S' si muove con velocità v rispetto ad un sistema S, e u' è la velocità misurata rispetto a S' lungo la direzione del moto, la velocità u misurata rispetto a S è:

u'+v

u= _________________

1+(u'v/c^2)

Ancora una volta, vediamo che se u' e v sono molto piccole, la formula si avvicina formalmente a quella enunciata da Galileo. Possiamo anche notare come c sia la massima velocità concepibile: sostituendo c al posto di u', v o ad entrambe, infatti, si ottiene proprio u=c. Ma quali sono le conseguenze di tali "stranezze"? Einstein a proposito realizzò alcuni esperimenti mentali per mettere in luce assurdità e contraddizioni della sua teoria, che comunque ebbe numerosissime conferme sperimentali. E' celeberrimo, ad esempio, il paradosso dei gemelli: se uno di loro viaggiasse nello spazio per molti anni alla velocità della luce, troverebbe al suo ritorno il fratello molto più vecchio di lui, perché a quelle velocità il tempo scorre più lentamente. Ecco trovato un modo assolutamente naturale per rimanere giovani ed evitare la chirurgia estetica! L'esperimento del garage, invece, mette in luce come in effetti non esista un'unica realtà oggettiva concreta e misurabile, ma esistono invece tante realtà quanti sono i punti di vista che la contemplano. Immaginiamo un automobile lunga 3 metri e un garage, anch'esso lungo 3 metri, munito di porte automatiche su entrambe le pareti di fondo. Se l'autista incoscientemente entrasse nel garage alla velocità della luce, vedrebbe quest'ultimo più corto e quindi l'auto sporgerebbe da entrambe le uscite con le porte aperte; un osservatore nel garage, invece, vedrebbe l'auto più corta entrare nel garage consentendo la chiusura delle porte. La cosa incredibile è che entrambi hanno ragione.

Esiste anche una misurazione "concreta" di questi effetti: i muoni, ad esempio, sono prodotti dal decadimento di altre particelle nell'alta atmosfera. Questi muoni sono rilevabili sulla terra, ma vista la loro vita media brevissima, anche se viaggiano a velocità relativistiche in teoria dovrebbero percorrere solo 600 metri circa, non facendo in tempo ad arrivare sulla superficie terrestre. Ma la dilatazione dei tempi consente invece loro di percorrere parecchi chilometri e di arrivare fino ai rilevatori posti sulla terra. La teoria della Relatività Ristretta presuppone l'esistenza di una realtà a 4 dimensioni contro le 3 "classiche": la quarta corrisponde al tempo. Spazio e tempo, quindi, non solo non sono assoluti, ma non sono neanche indipendenti l'uno dall'altro: formano, al contrario, un'unica entità che Minkovski definì "cronotopo".

La Relatività Generale

La Relatività Generale fu pubblicata nel 1916 ancora una volta da Albert Einstein; questa teoria si occupa delle osservazioni di corpi ed eventi in ogni sistema di riferimento, anche in quelli non inerziali. Si capisce, quindi, che la relatività ristretta è un caso particolare di quella generale. Ciò è reso possibile dal principio di equivalenza, in base al quale un sistema inerziale immerso in un campo gravitazionale è del tutto equivalente ad un sistema non inerziale (quindi accelerato) non permeato da alcun campo. Ne consegue che non c'è alcuna differenza qualitativa fra sistemi inerziali e non, e anche che massa inerziale e massa gravitazionale sono equivalenti. Ma quali sono gli aspetti della realtà che vengono messi in luce dalla relatività generale? Innanzitutto la massa perde la propria caratteristica di essere immutabile: Einstein dimostrò che se m è la massa di un corpo misurata quando esso è in quiete rispetto all'osservatore e m' è la massa misurata da un altro osservatore in moto con velocità v rispetto al corpo stesso, tra m e m' sussiste la relazione:

m

m'= ______________

√(1-v^2/c^2)

A basse velocità la variazione della massa è trascurabile, mentre a velocità relativistiche si ha un incremento consistente. Un'altra radicale novità si ha nel fatto che esiste un'equivalenza fra massa ed energia. La massa è quindi una forma di energia allo stato potenziale: un corpo può perdere massa trasformandola in energia, o analogamente una quantità di energia può trasformarsi in massa. La relazione che esiste fra l'energia persa (o acquistata) e la massa acquistata (o persa) è:

E=mc^2

Un'importante conseguenza del principio di equivalenza è l'inesistenza di una forza gravitazionale di tipo newtoniano: l'apparente attrazione fra due corpi in realtà è dovuta alla curvatura che ogni oggetto dotato di massa provoca sul cronotopo: la traiettoria di due corpi in questo spazio curvo è tale da farli avvicinare. Una famosa metafora è quella del telo: se su di esso si pone una massa si crea una deformazione; un altro corpo appoggiato sullo stesso telo inevitabilmente "scivola" verso l'altra massa. Il cronotopo, quindi, non è indipendente neanche dalla massa. Per descrivere correttamente questo nuovo spazio curvo, Einstein, tra l'altro, si servì della geometria di Bernhard Riemann, che negava alcuni postulati di Euclide e concepiva, appunto, uno spazio curvo: in tale geometria, ad esempio, la linea più breve fra due punti è la "geodetica", non il segmento, ed è inoltre possibile costruire triangoli con due angoli retti.

La Meccanica Quantistica

Max Planck

Il primo passo verso l'elaborazione di questa teoria si ebbe il 14 dicembre del 1900, quando Max Planck risolse un problema circa la radiazione emessa da un corpo nero. Sperimentalmente si sapeva che il grafico che rappresentava l'andamento della radianza spettrale (potenza emessa dal corpo per unità di superficie) in funzione della frequenza emessa aveva una forma a "campana". Ciò era inspiegabile con la fisica classica, secondo la quale la radianza sarebbe dovuta tendere a infinito, e non a zero, al crescere della frequenza:

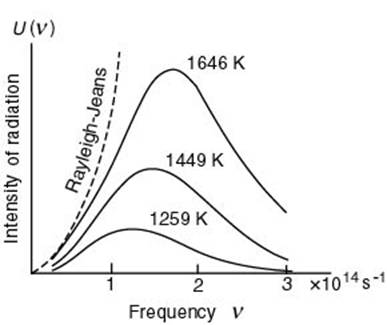
Andamento della radianza spettrale in funzione della frequenza:la linea tratteggiata è l'andamento previsto dalla fisica classica; le linee continue, invece, rappresentano l'andamento reale, che è in accordo con la formula trovata da Planck

Planck quel fatidico giorno propose una formula che legava la radianza R alla frequenza f e alla temperatura assoluta T:

hf^3

R(f,T)= ____*_____________

c^2 e^(hf/kbT)-1

Qui apparse per la prima volta una nuova costante fondamentale, chiamata costante di Planck, il cui valore è h=6,626*10^(-34). Tale formula era in perfetto accordo con l'esperienza a patto che l'energia scambiata da una particella oscillante con la radiazione fosse considerata una quantità ben definita, un "quanto" di energia. Lo scambio di energia, in altre parole, doveva essere "discreto" e non "continuo" come si credeva in precedenza: ogni quantità di energia doveva essere considerata multiplo intero di una quantità fondamentale. Il "salto" di energia è legato alla frequenza della radiazione da questa formula:

∆E=hf

Questa idea sconvolgente non fu accolta con favore fino a quando Einstein, per spiegare l'effetto fotoelettrico (emissione di elettroni da una lastra metallica in seguito all'assorbimento di una radiazione) dimostrò che un'onda elettromagnetica si può considerare come una corrente di "fotoni", ognuno con energia E=hf. Da tutto ciò deriva l'idea che ogni atomo abbia un proprio "stato quantico"; come dimostrò Bohr, infatti, gli elettroni attorno al nucleo possono trovarsi solo in particolari zone chiamate "orbitali", ognuna con un proprio livello di energia, e ogni elettrone, inoltre, non può trovarsi in uno stato intermedio, ma solo procedere per "salti". In base a questi primi risultati Bohr enunciò il "principio di corrispondenza", in base al quale non si poteva applicare la meccanica classica su scale atomiche, ma bisognava invece trovare un modello "quantistico" le cui conseguenze sconcertanti diventassero trascurabili (come in effetti sono) a livello macroscopico. Successivamente si dimostrò come non solo l'energia, ma anche spazio e tempo fossero quantità "discrete". Esistono, cioè, intervalli di tempo e lunghezze al di sotto delle quali non si può andare se non rinunciando a tutte le leggi della fisica oggi conosciute: probabilmente non è nemmeno lecito pensare che la fisica sia potenzialmente in grado di descrivere la realtà in quelle condizioni. Queste grandezze sono dette "spazio e tempo di Planck", e valgono rispettivamente 1,6*10^-35 m e 5*10^-44 s. Ma le novità non erano finite qui. Nel 1924 Luis De Broglie, vista la dualità onda-corpuscolo messa in evidenza da Einstein circa la luce, ipotizzò che ciò valesse anche per la materia. Egli calcolò che ogni particella materiale di massa m e velocità v ha anche una propria lunghezza d'onda che vale:

h

λ= ____

mv

Successivi esperimenti dimostrarono che la natura ondulatoria o corpuscolare della luce e delle particelle (in particolare gli elettroni) emerge escludendo l'altra a seconda dell'esperimento condotto: se si fanno passare elettroni o fotoni attraverso due strette fenditure si rileva su un apposito schermo una figura d'interferenza tipica di un onda, ma se si chiude una delle due fenditure per capire da dove viene quel fotone o quell'elettrone la figura d'interferenza scompare, facendo dedurre che in quest'ultimo caso è prevalsa la natura particellare su quella ondulatoria. Bohr generalizzò i risultati enunciando il "principio di complementarietà", secondo cui in un esperimento, se emerge un aspetto di un fenomeno fisico, è impossibile registrare l'altro aspetto ad esso complementare. I due aspetti in questione, quindi, si completano, ma insieme si escludono. Schrodinger formalizzò i risultati di De Broglie attraverso un'"equazione d'onda", estremamente complessa, che descrive lo stato di una particella o di un sistema e il suo evolversi nel tempo. Ma questa equazione non porta ad un risultato preciso, bensì fornisce una "densità di probabilità", cioè descrive solo la regione di spazio in cui è più probabile trovare una data particella in un dato istante. Tutte le probabilità, naturalmente, si riducono ad una sola se si riesce ad osservare la particella in questione. La conseguenza più immediata è che gli orbitali atomici non si possono considerare come orbite ben definite, ma come "nuvole" in cui è più alta la possibilità di trovare l'elettrone. Viene così a crollare il mito del determinismo tanto importante nella fisica classica. Per meglio far comprendere la portata di tale innovazione, Schrodinger propose l'esempio del "gatto": se l'animale viene chiuso in una stanza in cui un dispositivo che emette un veleno mortale può funzionare solo in seguito ad un evento quantistico non prevedibile ma assolutamente casuale (come, ad esempio, il decadimento di un nucleo radioattivo), finche una persona non entra nella stanza il gatto è contemporaneamente vivo e morto: solo se viene osservato il gatto questo è certamente vivo oppure morto. Le probabilità, quindi, si riducono in caso di osservazione: ma Heisenberg, con il suo "principio di indeterminazione", dimostrò che è impossibile effettuare una misurazione precisa e che in ogni registrazione c'è sempre un'incertezza. In particolare, questo principio afferma che se si vuole determinare simultaneamente la posizione x e la quantità di moto qx di una particella lungo una data direzione, le incertezze ∆x e ∆qx sono legate dalla relazione:

h

∆x∆qx ≥ ____

Inoltre, per misurare l'energia E di una particella in un tempo ∆t, l'incertezza ∆E è tale che:

h

∆E∆t ≥ _____

2π

Quindi, più si cerca di conoscere meglio la posizione di una particella e meno si conosce la sua quantità di moto; lo stesso vale per la sua energia e l'istante in cui la particella possiede quell'energia.. Queste coppie di grandezze si dicono "coniugate": vuol dire che per descrivere lo stato di un corpo bisogna conoscerle entrambe. Ciò viene irrimediabilmente precluso da questo principio, che stabilisce un'impossibilità di misurazione "a priori", e non per motivi tecnici, come si credeva nella fisica classica. Una conseguenza paradossale di queste scoperte è il cosiddetto "effetto tunnel". Secondo la fisica classica un corpo non può mai attraversare una "barriera di potenziale", cioè una zona in cui l'energia totale di un campo di forze supera l'energia del corpo stesso. A livello quantistico, invece, se la barriera è limitata, esiste una possibilità seppur piccola che la particella si trovi al di là della barriera: questo in base alle equazioni di Schrodinger. Può accadere, quindi, che la particella attraversi senza problemi la barriera come se la attraversasse in un tunnel. Infatti, secondo il principio di determinazione, in un tempo brevissimo l'energia può fluttuare così tanto da poter diventare maggiore di quella della barriera. L'effetto tunnel oggi trova un'applicazione diretta nei circuiti elettrici di ultima generazione. Un altro fenomeno quantistico molto interessante è quello dell'entanglement, cioè "legame". Se due particelle sono entangled, ogni modifica operata allo stato quantico di una particella si realizza istantaneamente anche allo stato dell'altra, a prescindere dalla loro distanza. Gli studiosi più pionieristici a proposito parlano di un vero e proprio "teletrasporto". Questo fenomeno è ancora per molti aspetti oscuro, ma potrebbe trovare un'applicazione efficace nel "computer quantistico", la cui velocità sarebbe molto maggiore rispetto a quella degli odierni processori.

Bisogna dire che tutte le incredibili stranezze del mondo dei quanti diventano impercettibili su scale macroscopiche, così come i paradossi della relatività svaniscono a basse velocità. C'è però una contraddizione fra le due teorie per quanto riguarda la gravità: mentre la Relatività la considera una conseguenza della distorsione dello spazio-tempo, la Meccanica Quantistica presuppone invece l'esistenza di un "mediatore" di forza, una particella chiamata "gravitone" o "bosone di Higgs", ancora sconosciuta, ma che potrebbe rivelarsi al grandioso esperimento previsto al LHC del CERN di Ginevra. Solo una "Teoria del Tutto" potrebbe giungere ad un compromesso fra queste due posizioni.

Si può concludere dicendo che, dal punto di vista fisico, il "senso comune" dell'uomo è legittimo solo se impiegato per comprendere la ristretta vita quotidiana, mentre è destinato al fallimento se si cerca di andare "oltre".