Percorsi tra due punti di una sfera
Individuati due punti, è definita rotta il
percorso che li congiunge. Possiamo definire due tipi di rotta:
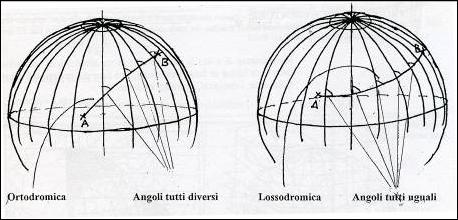La prima è un arco di circolo massimo ed è il percorso più breve che
congiunge i due punti (equivalente al segmento per due punti del piano).
Infatti sappiamo che l'intersezione tra il piano individuato tra due punti
della superficie sferica e dal centro della sfera è un circolo massimo, detto ortodromia.
Il minor arco di ortodromia tra i due punti dati costituisce il percorso
ortodromico o rotta ortodromica.
Poiché i meridiani muovendo verso i poli si
avvicinano tra loro, allora l'angolo che l'ortodromia fa con essi varia continuamente
(a meno che essa non coincida con un meridiano o con l'equatore). Da ciò segue
che per navigare lungo un percorso ortodromico si dovrebbe cambiare l'angolo di
rotta ad ogni istante.
La seconda è una spirale (concava verso i
poli) sulla superficie della sfera e non è il percorso più breve tra i due
punti. Tuttavia è molto utilizzata nella navigazione in quanto essa mantiene un
angolo costante con tutti i meridiani ad ogni latitudine.
Tutto ciò, ovviamente, non viene calcolato
direttamente sulla superficie del mare, bensì utilizzando le carte nautiche che
sono proiezioni in piano ella superficie della sfera terrestre.
Le proiezioni più usate per la navigazione
sono la gnomonica e quella detta di Mercatore.
La proiezione gnomonica serve per tracciare rotte ortodromiche, unendo
con una linea retta i due estremi del percorso. Viene perciò utilizzata per le
grandi distanze come quelle di navigazione oceanica o per zone molto ridotte,
come l'interno dei porti, od ancora per le zone polari che non possono essere
rappresentate altrimenti.
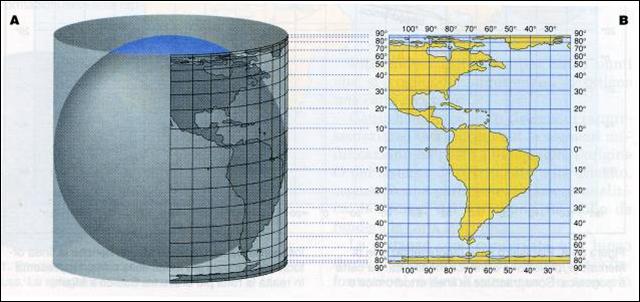
La proiezione di mercatore è una proiezione
cilindrica modificata, già costruita nel XVI secolo dall'olandese Mercator, in
cui i meridiani sono rette parallele mentre i paralleli sono disegnati a
intervalli sempre maggiori via via che si procede verso i poli. I poli,
infatti, non sono rappresentabili in quanto si sono dilatati fino alla
dimensione dell'equatore. Le regioni rappresentate in queste carte sono
notevolmente deformate, specie quelle vicino ai poli, ma questo tipo di carte
consente di tracciare le rotte lossodromiche come segmenti congiungenti due
punti, il che è molto vantaggioso se la navigazione non è effettuata per
distanze eccessive. Per meglio comprendere come si crea la proiezione di
Mercatore si può immaginare di avvolgere un cilindro attorno alla terra e poi
svolgerlo. Naturalmente le carte di Mercatore che si trovano all'Istituto
Idrografico sono ottenute mediante modelli matematici.
[ Picolo appunti ]
