 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2693 | Gradito: |
Leggi anche appunti:La fusione - "quando l'uomo creo il sole"La Fusione "Quando L'uomo creo IL sole" All'inizio del ventesimo secolo Felix Christian Klein (1849-1925)Felix Christian Klein (1849-1925) Di origine tedesca, studiò matematica L'esperimento di MillikanL'esperimento di Millikan Il diagramma mostra una versione semplificata dell'apparato |
 |
 |
Le trasformazioni di Lorentz-Einstein
Si considerino due sistemi di riferimento inerziali K e K', vedi fig(10-a), in moto relativo con velocità v e tali per cui all'istante t=0 si ha O=O' ed inoltre gli assi x ed x' siano coincidenti e paralleli al vettore velocità. Non è riduttivo porre queste condizioni che serviranno a facilitare il calcolo in quanto lo Spazio-Tempo è omogeneo e continuo e non vi è nessuna direzione o istante di tempo privilegiato. I risultati trovati, dunque, avranno valore generale. Per derivare le trasformazioni di Lorentz utilizzeremo un metodo che prevede l'eliminazione di alcuni coefficienti mediante l'applicazione di alcune leggi fondamentali della Fisica. Partendo dall'omogeneità dello Spazio-Tempo la prima condizione da porre è che le equazioni che descrivono il passaggio da un sistema di coordinate ad un altro siano lineari, ossia di primo grado. Se per ipotesi, x' dipendesse dal quadrato di x, non vi sarebbe un valore univoco che descriva il cambiamento di coordinate.
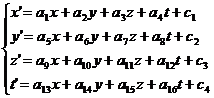
Possiamo porre ![]() senza perdere in
generalità. Ciò equivale ad assumere che all'istante
senza perdere in
generalità. Ciò equivale ad assumere che all'istante![]()
![]() . Essendo in uno Spazio-Tempo con tensore di curvatura di
Riemann pari a 0 deduciamo che il parallelismo si mantiene e siccome abbiamo
stabilito che il moto avvenga parallelo agli assi x ed x' se y=0 e z=0 (per semplicità) allora anche y'=0 e z'=0, quindi per
sostituzione nella 37) si ha:
. Essendo in uno Spazio-Tempo con tensore di curvatura di
Riemann pari a 0 deduciamo che il parallelismo si mantiene e siccome abbiamo
stabilito che il moto avvenga parallelo agli assi x ed x' se y=0 e z=0 (per semplicità) allora anche y'=0 e z'=0, quindi per
sostituzione nella 37) si ha:
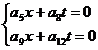
Siccome queste
equazioni devono essere valide ![]() è ovvio che i
coefficienti
è ovvio che i
coefficienti ![]() saranno tutti sempre
uguali a 0, quindi otteniamo:
saranno tutti sempre
uguali a 0, quindi otteniamo:

Il parallelismo si mantiene, oltre che per le rette, anche per i piani, in particolare xy e xz dovranno coincidere con x'y' e x'z', di conseguenza ancora una volta si ha che y=0 e z=0; y'=0 e z'=0:

segue:

Determiniamo
![]() utilizzando il
principio di relatività. Poniamo in K
un'asta rigida di lunghezza 1. Un osservatore posto in K' misura l'asta che ha per lui lunghezza:
utilizzando il
principio di relatività. Poniamo in K
un'asta rigida di lunghezza 1. Un osservatore posto in K' misura l'asta che ha per lui lunghezza:![]() . Ipotizziamo di porre una seconda asta della stessa
lunghezza in K' e chiediamo ad un
osservatore posto in K di misurarla:
. Ipotizziamo di porre una seconda asta della stessa
lunghezza in K' e chiediamo ad un
osservatore posto in K di misurarla: ![]() . Siccome per l'enunciato di Einstein le lunghezze ortogonali
al moto non subiscono contrazioni, si ottiene:
. Siccome per l'enunciato di Einstein le lunghezze ortogonali
al moto non subiscono contrazioni, si ottiene:
![]()
Utilizzando la stessa dimostrazione per z e z' si giunge ad affermare:
![]()
quindi sostituendo nel sistema:
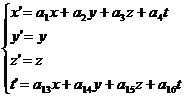
Determiniamo i coefficienti di t'. Per l'isotropia dello Spazio-Tempo supponiamo che t' non dipenda né da y né da z, altrimenti t' sarebbe in funzione di due direzioni traverse quando noi sappiamo essere la direzione parallela al moto relativo l'unica direzione fisicamente rilevante, dunque:
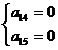
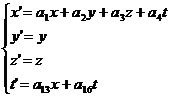
Consideriamo
l'equazione per x'. Sappiamo che
l'origine O' si muove rispetto ad O con velocità v, quindi in un tempo t
percorre una distanza pari a vt.
Immaginiamo che l'evento coincida con l'origine, allora ad ![]() dovrà corrispondere
dovrà corrispondere ![]() , il che implica:
, il che implica:

ma anche:
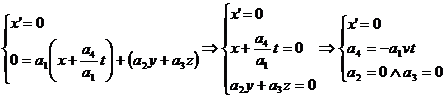
quindi infine:
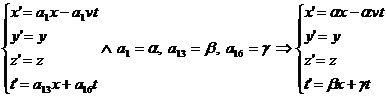
Queste equazioni devono ora rispettare un'importantissima condizione: devono mantenere invariato l'intervallo spaziotemporale per cui:
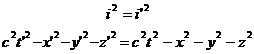
Proponiamo qui di seguito i dettagli dei calcoli:

In virtù della condizioni poste dalla 50):
![]()
Affinché questa uguaglianza venga verificata si dovrà porre:
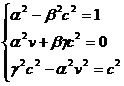
risolviamo il sistema:
(segue nella pagina successiva)
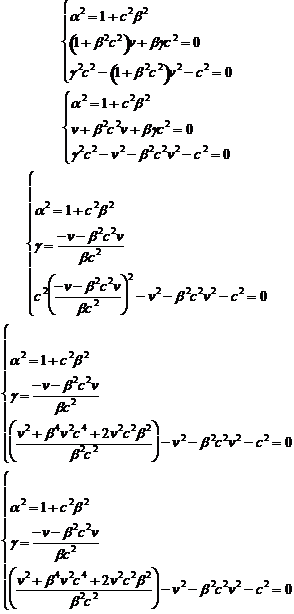
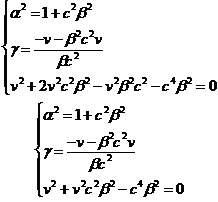

Sostituendo infine nella 49 otteniamo le trasformazioni di Lorentz-Einstein:

Oppure le stesse trasformazioni in forma matriciale:
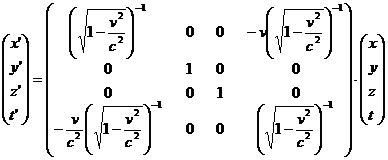
 |
| Appunti su: trasformazioni di lorentz dimostrazione, cambiamento di coordinate trasformazioni fondamentali, |
|
| Appunti Geografia |  |
| Tesine Chimica |  |
| Lezioni Biologia |  |