 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2229 | Gradito: |
Leggi anche appunti:Marie Curie (1867-1934)Marie Curie (1867-1934) Marie Sklodowska con suo marito Pierre Curie, Il principio di indeterminazioneIl principio di indeterminazione Par. 1) I problemi della misurazione In Teoria della relatività ristrettaTeoria della relatività ristretta 1.1 Le |
 |
 |
La teoria della relatività ristretta
Par. 1) I postulati
Nel 1905 Albert Einstein pubblicò la sua teoria della relatività speciale o ristretta, valida per i sistemi in moto rettilineo uniforme l'uno rispetto all'altro. La teoria di Einstein è basata su due postulati:
PRIMO POSTULATO: il principio di relatività
Le leggi della fisica sono le stesse in tutti i sistemi di riferimento inerziali.
SECONDO POSTULATO: la costanza della velocità della luce
La velocità della luce nel vuoto è c=![]() m/s in tutti i sistemi di riferimento inerziali,
indipendentemente dal moto della sorgente rispetto all'osservatore.
m/s in tutti i sistemi di riferimento inerziali,
indipendentemente dal moto della sorgente rispetto all'osservatore.
Par. 2) Lo spazio e il tempo
Nella fisica classica lo spazio ed il tempo sono considerate grandezze fondamentali e non hanno particolari relazioni. Nella teoria della relatività invece, spazio e tempo sono strettamente legati e costituiscono le coordinate di un evento in uno "spazio" quadridimensionale. Grazie all'aiuto del suo professore di matematica, Einstein riuscì a esprimere con leggi numeriche le relazioni tra spazio e tempo che aveva teorizzato. Per rappresentare gli eventi nello spazio-tempo (o cronotopo) egli usava un diagramma cartesiano ortogonale in cui
a) in ascissa sta una delle coordinate spaziali x
b) in ordinata sta il tempo t, espresso in metri grazie alla relazione z=ct dove z è lo spazio
Nel diagramma spazio-tempo una sequenza può essere espressa mediante una linea, chiama linea di universo, i cui punti visualizzano istante per istante la posizione nello spazio dell'entità considerata. In ►fig.1 è rappresentato un diagramma spazio-tempo con le linee di universo di un oggetto fermo (azzurro), di un raggio di luce (rosso) e di un oggetto in moto con velocità v tale che v<c (verde).
figura 2

Come si può osservare, l'oggetto fermo non muta la sua coordinata spaziale x al trascorrere del tempo, mentre il raggio di luce percorre ogni secondo una distanza Δx=c Δt: la sua linea di universo è allora ovviamente la bisettrice del quadrante. Infine l'oggetto in moto percorre una distanza minore rispetto a quella del raggio di luce, a parità di tempo trascorso.
Par. 3) La simultaneità
In generale, due eventi si dicono simultanei quando accadono nello stesso istante. La registrazione di un evento può però avvenire soltanto quando quest'ultimo viene percepito, e quindi quando la luce ha percorso la distanza che separa evento ed osservatore. Il concetto pare eccessivo se pensato sulla Terra, ma non lo è se consideriamo le stelle visibili nell'universo: un fenomeno relativo ad un astro che viene osservato si è in realtà verificato t=d/c secondi prima della sua manifestazione (dove d è la distanza stella-osservatore). Per sincronizzare due orologi, dunque, bisogna tener conto della distanza che li separa dal luogo in cui accade l'evento.
Due eventi, inoltre, possono essere giudicati simultanei da un osservatore, e possono essere invece giudicati non simultanei da un altro osservatore in moto uniforme rispetto al primo. Per spiegare tali concetti, Einstein ricorreva a degli "esperimenti mentali", uno dei quali è qui di seguito riportato.
Supponiamo di predisporre un vagone ferroviario che si muove di velocità v costante rispetto al suolo e fornito di due orologi sincronizzati (posizionati alle estremità interne del vano) per un osservatore O' al centro del vagone. Nello stesso luogo dell'osservatore è posta una sorgente luminosa; se l'osservatore O' accende la sorgente, la luce andrà a colpire i due orologi e se questi ultimi sono in grado di registrare in che istante vengono raggiunti dal fascio luminoso, segneranno il medesimo momento grazie alla loro sincronizzazione (►fig.3a).
Un osservatore O, esterno al vagone e solidale col terreno, osserva lo stesso evento ma registra l'esperienza mediante due orologi sincronizzati per il suo sistema di riferimento. Anche per O la luce si muove in tutte le direzioni ma la testa del vagone si allontana con velocità v dal fronte d'onda della luce, mentre la coda si avvicina ad esso con la stessa velocità. Conseguentemente l'orologio di coda sarà colpito prima dalla luce e segnerà un tempo diverso da quello di testa (►fig.3b).
figura 3 b) a)

L'esperienza vuole dimostrare che anche il tempo è un concetto relativo, e dipende dal sistema di riferimento dal quale si osserva un evento.
Par. 4) La dilatazione del tempo
Secondo la teoria della relatività può
mutare, oltre all'istante in cui avviene, anche la durata di un evento, a
seconda delle condizioni dell'osservatore. Ricorriamo ad un altro esperimento
mentale riportato in ►fig.4 . Supponiamo
che un'astronave A sia in moto con
velocità v rispetto alla Terra, sulla
superficie della quale è posto un osservatore O; nell'astronave c'è invece un osservatore O', ed è allestito un esperimento: una sorgente luminosa L emette un rag
![]()
Poiché per l'osservatore terrestre l'astronave è in movimento, per raggiungere lo specchio e per tornare indietro la luce dovrà compiere un tragitto più lungo (►fig.4b). Nel tempo Δt (impiegato dalla luce per andare e tornare) infatti, l'astronave compie uno spostamento pari a 2l=v Δt e la luce percorre uno spazio s dato da
![]()
a)
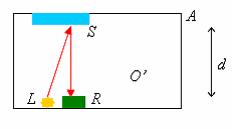
figura 4 b)

Elevando al quadrato membro a membro la , tenendo conto della e risolvendo rispetto a Δt si ottiene la seguente proprietà:
RELAZIONE FRA INTERVALLI DI TEMPO MISURATI DA OSSERVATORI IN MOTO RELATIVO
Se Δt' è l'intervallo di tempo fra due eventi, misurato da un osservatore per il quale essi accadono nello stesso punto dello spazio, l'intervallo di tempo Δt fra gli stessi eventi, misurato in un secondo sistema in moto rettilineo uniforme con velocità di modulo v rispetto al primo è:
![]()
In tale relazione Δt' è detto anche tempo proprio. La precedente proprietà rappresenta la dilatazione del tempo, in contrasto con la concezione assoluta dello stesso postulata dalla fisica classica.
Par. 5) La contrazione delle lunghezze
Per mostrare che anche lo spazio è una grandezza relativa, Einstein ricorreva ad un altro esperimento mentale. Supponiamo che un'astronave A viaggi con velocità v dalla Terra verso Plutone (►fig.5). L'osservatore O' che sta sull'astronave assegnerà al viaggio un tempo di durata Δt', mentre un osservatore O situato sulla Terra registrerà, per quanto visto nel paragrafo precedente, un tempo Δt più lungo. Per la i due intervalli di tempo sono legati dalla seguente relazione:
![]()
figura 5
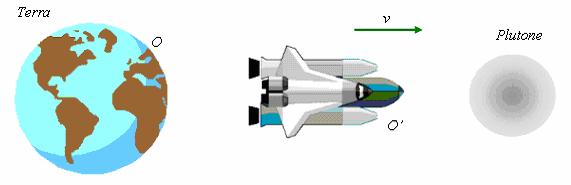
Se indichiamo con l e l' la distanza Terra-Plutone rispettivamente per O e O' si ha che:
l'=vΔt'
l=vΔt
Dividendo membro a membro e risolvendo rispetto a l' si ottiene la seguente proprietà:
RELAZIONE FRA DISTANZE MISURATE DA OSSERVATORI IN MOTO RELATIVO
Se l è la distanza tra due punti misurata da un osservatore in quiete rispetto ad essi, la distanza l' fra gli stessi punti, valutata da un secondo osservatore in moto rettilineo uniforme con velocità di modulo v rispetto al primo, è:
![]()
In tale relazione l è detta anche lunghezza propria. La precedente proprietà rappresenta la contrazione delle lunghezze, che si verifica solo nella direzione del moto e non riguarda dunque le dimensioni trasversali di un oggetto.
Par. 6) La composizione delle velocità
Nella fisica classica, se un'astronave in
moto rispetto alla Terra con velocità ![]() contiene un corpo il
quale si muove rispetto all'astronave con velocità
contiene un corpo il
quale si muove rispetto all'astronave con velocità ![]() nella stessa direzione
dell'astronave stessa, la velocità effettiva del corpo rispetto alla Terra è
nella stessa direzione
dell'astronave stessa, la velocità effettiva del corpo rispetto alla Terra è ![]() . Se la velocità dell'astronave fosse però
. Se la velocità dell'astronave fosse però ![]() e quella del corpo
fosse
e quella del corpo
fosse ![]() , quest'ultimo si muoverebbe con velocità
, quest'ultimo si muoverebbe con velocità ![]() superiore a quella
della luce (assurdo). Inoltre, se il corpo all'interno dell'astronave fosse una
sorgente luminosa, la luce emessa avrebbe una propria velocità rispetto
all'astronave pari a
superiore a quella
della luce (assurdo). Inoltre, se il corpo all'interno dell'astronave fosse una
sorgente luminosa, la luce emessa avrebbe una propria velocità rispetto
all'astronave pari a ![]() e una velocità finale
rispetto alla Terra pari a
e una velocità finale
rispetto alla Terra pari a ![]() . Questo risultato è però in contraddizione con i postulati
della relatività.
. Questo risultato è però in contraddizione con i postulati
della relatività.
La composizione delle velocità non può allora avvenire mediante le trasformate di Galileo, ma tramite le trasformazioni di Lorentz. Da queste ultime infatti, con opportune considerazioni, è possibile ricavare la seguente proprietà:
ADDIZIONE DELLE VELOCITA'
Se in un sistema inerziale S' si
muove rispetto ad un altro sistema S con velocità costante di modulo v e se ![]() è la velocità di un
corpo che si sposta nella direzione del moto relativo dei due sistemi, misurata
in S', la velocità dello stesso corpo, misurata in S, è:
è la velocità di un
corpo che si sposta nella direzione del moto relativo dei due sistemi, misurata
in S', la velocità dello stesso corpo, misurata in S, è:
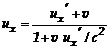
E' interessante notare che se nella v e ![]() sono grandezze
piccole, il quoziente
sono grandezze
piccole, il quoziente ![]() tende a zero e il
denominatore tende ad 1. Pertanto la
relazione assume la forma delle trasformate di Galileo, valide dunque per
piccole velocità.
tende a zero e il
denominatore tende ad 1. Pertanto la
relazione assume la forma delle trasformate di Galileo, valide dunque per
piccole velocità.
Par. 7) Conseguenze della relatività ristretta
Una delle conseguenze più famose della relatività è il paradosso dei gemelli. Presi due individui nati nello stesso momento, infatti, imbarcatone uno su un'astronave capace di viaggiare a velocità prossime a quelle della luce e lasciato l'altro a terra, per l'individuo in viaggio il tempo si dilata e scorre più lentamente, lasciando l'essere vivente in moto più giovane rispetto al suo coetaneo sulla Terra. La veridicità di questo fenomeno è stata dimostrata nel 1971 da J. C. Hafele e R. E. Keating: utilizzando orologi atomici al cesio, portati in volo attorno al mondo con un aereo e confrontati con uguali orologi a terra, i due ricercatori scoprirono che gli orologi in volo erano restati in anticipo rispetto a quelli rimasti a terra.
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Chimica |  |
| Lezioni Biologia |  |