 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2728 | Gradito: |
Leggi anche appunti:La fisica particellareLa fisica particellare Par. 1) La struttura ultima della materia Una Cenni sull'ellissoideCenni sull'ellissoide Finora abbiamo considerato la Terra come un corpo ProprietÀ magnetiche dei materialiPROPRIETÀ MAGNETICHE DEI MATERIALI Esistono diverse classificazioni dei |
 |
 |
IL BARICENTRO

Ricordiamo che qualunque corpo dotato di massa, in presenza della gravitazione terrestre, è anche "dotato" di una forza peso diretta verticalmente verso il basso; se la massa del corpo è m, allora la forza peso cui è sottoposto è
P = m 9,8 N (2.7.1)
oppure
P = m Kgp (2.7.2)
ESEMPIO: qual è la forza peso cui è sottoposto un corpo con la massa di 100 Kg?
P = 100 Kg 9,8 m/s2 = 980 N
oppure
P = 100 Kgp.
Se il corpo da 100 Kg è piccolo e sferico siamo portati a dire che la forza peso da 980 N è applicata al centro della sfera; e se il corpo non è rappresentabile da un punto materiale?
Possiamo supporre qualunque corpo fisico esteso come formato da tante piccole masse rappresentabili da sferette o da punti "pesanti"; su ciascuna di queste sferette elementari agirà un vettore forza peso diretto verticalmente verso il basso (fig. 2.7.1).
Cercare la posizione del punto di applicazione della forza peso totale di un corpo equivale dunque a cercare la posizione della risultante di tanti vettori paralleli e concordi agenti su un corpo.
Chiameremo questa posizione baricentro (centro dei pesi) del corpo:
un corpo esteso e pesante si comporta (ai fini della forza di gravità) come se tutta la sua massa fosse concentrata in quel punto.
Nel caso le forze peso agenti sul sistema siano solo due, il problema della determinazione del baricentro lo sappiamo già risolvere grazie all'equazione (2.6.1).
ESEMPIO: un corpo è formato da due masse m1=10 Kg e m2=100 Kg poste agli estremi di una asta di legno di lunghezza 10 metri e peso trascurabile. Quanto vale la risultante delle due forze peso? Dove si posiziona?
Alla massa m1 è associato un peso di 10 9,8 = 98 N; alla massa m2 un peso di 100 9,8= 980 N.
La risultante R varrà 980+98= 1078 Newton e sarà più vicina alla massa da 100 Kg. Se x è la distanza dai 100 Kg allora (10-x) è la distanza dai 10 Kg.
(10-x) = 980 x 980 - 98 x = 980 x 980 = 1078 x x = 980/1078 = 0,9 m
Il baricentro si collocherà dunque a 0,9 metri dalla massa da 100 Kg e l'asta con le due masse agli estremi si comporterà (ai fini del peso) come un solo punto materiale lì posizionato e "pesante" 1078 N.
Se i "punti" di cui è fatto il corpo sono più di due bisogna applicare il metodo dei due punti più volte:
si determina il baricentro di due punti trovando un primo baricentro parziale, e poi si trova il baricentro tra questo baricentro parziale ed un terzo punto...
 A parte un eventuale
problema di calcoli basta comunque sapere che qualunque corpo pesante è dotato
di un baricentro e che, ai fini della gravità, il corpo si comporta come se
tutta la massa fosse lì concentrata.
A parte un eventuale
problema di calcoli basta comunque sapere che qualunque corpo pesante è dotato
di un baricentro e che, ai fini della gravità, il corpo si comporta come se
tutta la massa fosse lì concentrata.
Problema: determinare il baricentro del grappolo d'uva di fig. 2.7.1.
Svolgimento: sarebbe un utile esercizio in vista del compito..
Il baricentro soddisfa le seguenti regole pratiche:
si colloca sugli assi di simmetria
si colloca più vicino alle masse più grandi.
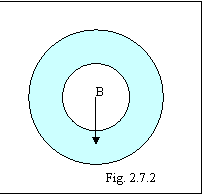
NOTA BENE: il baricentro di un corpo può essere collocato anche esternamente al corpo. Il baricentro di un anello, per esempio, è collocato al centro dell'anello essendo questo un centro di simmetria.
 |
| Appunti su: riassunto ome ai determina il baricentro, |
|
| Appunti Chimica |  |
| Tesine Biologia |  |
| Lezioni Geografia |  |