 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 6511 | Gradito: |
Leggi anche appunti:Individuazione dei sali in un miscuglioINDIVIDUAZIONE DEI SALI IN UN MISCUGLIO OBIETTIVO: individuare Modulo di Metodi Fisici in Chimica OrganicaCorso di Metodi Fisici in Chimica Organica e Chimica Analitica Per Biotecnologie I Composti InorganiciI Composti Inorganici Ossidi : Metallo + Ossigeno = |
 |
 |
L'ipotesi di De Broglie fu generalizzata e formalizzata dal fisico austriaco E. Schrödinger, che nel 1926 ottenne un'equazione valida per il moto di una qualsiasi particella in un campo di forza, detta equazione d'onda Ψ (la lettera greca psi) o equazione di Schrödinger.
L'equazione d'onda, che descrive l'elettrone ha caratteristiche analoghe a quelle che descrivono le onde stazionarie nella meccanica classica. In entrambi i casi l'onda modifica la sua ampiezza passando alternativamente da valori positivi a negativi. I punti in cui il segno dell'onda cambia (da positivo a negativo o viceversa) e l'onda presenta ampiezza nulla si chiamano nodi.

L'equazione d'onda di Schrödinger può essere applicata anche ad atomi diversi da quello dell'Idrogeno e risolta (anche se attraverso approssimazioni) con risultati in buon accordo con i dati sperimentali.
Quando si risolve l'equazione d'onda per un atomo particolare si ottiene una equazione parametrica, detta funzione d'onda Y, che presenta come parametri i primi tre numeri quantici, n, l, m.
Una funzione d'onda alla quale vengano attribuiti opportuni valori numerici ai numeri quantici individua lo stato di un particolare elettrone e prende il nome di funzione orbitalica o funzione orbitale..
Ogni funzione orbitale corrisponde ad uno stato stazionario dell'elettrone-onda.
Schrödinger arrivò alla conclusione che l'equazione d'onda che descrive un oscillatore meccanico poteva essere applicata anche all'atomo. Ora in acustica se la frequenza fondamentale è x la frequenza della seconda, terza, quartaennesima armonica sarà 2x, 3x, 4xnx. In altre parole sarà sufficiente un solo parametro ( il numero intero positivo n = 1,2,3..) per individuare qualsiasi armonica.
Nel caso delle onde di Schrödinger il problema è più complesso poiché le onde in questione sono tridimensionali e sono necessari tre parametri per determinare una qualsiasi armonica. Tali parametri saranno anche in questo caso necessariamente quantizzati visto che l'onda in questione è un'onda vincolata e quindi stazionaria.
La natura ondulatoria dell'elettrone, 'vincolato' dal nucleo che lo attrae, rende l'atomo molto simile ad uno strumento musicale.
Tuttavia la meccanica che descrive le proprietà ondulatorie delle particelle quali l'elettrone differisce in modo sostanziale dalla meccanica classica ed è nota come meccanica quantistica.
La meccanica quantistica ci permette di ottenere informazioni su di una particella risolvendo l'equazione d'onda. L'informazione che si ottiene non è la posizione e la velocità della particella, ma la probabilità di trovarla in una determinata regione di spazio.
Dati certi valori ai numeri quantici n. l ed m, le soluzioni dell'equazione di Schrödinger non forniscono le coordinate del punto P in cui si dovrebbe trovare l'elettrone rispetto al nucleo posto idealmente all'origine degli assi, ma il valore che in quel punto assume la funzione d'onda
Ciò costringe ad abbandonare il concetto di traiettoria definita e quindi di orbita, per introdurre quello di orbitale, inteso come regione di spazio intorno al nucleo alla quale associare una certa probabilità di trovarvi l'elettrone.
Si può dunque descrivere il comportamento di un elettrone attorno ad un nucleo mediante la risoluzione dell'equazione di Schrödinger dove l'energia potenziale è quella esercitata da una carica positiva localizzata sull'origine (nucleo). Il sistema più semplice è l'atomo di idrogeno che contiene un solo elettrone ed è l'unico sistema per cui l'equazione di Schrödinger può essere risolta esattamente.
Come abbiamo già detto in precedenza, l'equazione d'onda che descrive il comportamento degli elettroni all'interno di un atomo presenta diverse soluzioni possibili, dette funzioni d'onda Ψ o funzioni orbitaliche o, semplicemente, orbitali. Gli orbitali s, p, d, f sono descritti da altrettante funzioni orbitaliche. Lo stato di un elettrone è descritto dalla funzione d'onda Ψ.
Tuttavia la funzione d'onda Ψ non ha significato fisico diretto. Si può invece dimostrare che la funzione Ψ2, nota come densità di probabilità fornisce la probabilità di trovare l'elettrone nell'unità di volume, in un determinata posizione dello spazio ad una data distanza dal nucleo ed è quindi proporzionale alla densità di carica presente.
Si noti l'analogia con la radiazione elettromagnetica, nel caso in cui si applichino grandezze caratteristiche del modello ondulatorio ad un singolo fotone. In un'onda elettromagnetica l'energia per unità di volume è proporzionale al quadrato dell'ampiezza dell'onda A2, dove l'ampiezza è data dall'intensità del campo elettrico o del campo magnetico ad esso concatenato. Se ora passiamo dal continuo al discreto e consideriamo la radiazione come un insieme di fotoni, A2 diventa una misura del numero di fotoni presenti nell'unità di volume e, per un singolo fotone, della probabilità di trovarlo nell'unità di volume.
Mentre Ψ può assumere anche valori negativi (l'ampiezza di un'onda può essere sia positiva che negativa), Ψ2 assume solo valori positivi (il quadrato di un valore negativo è sempre positivo ed una probabilità negativa non ha senso)
Le funzioni d'onda più semplici sono quelle che descrivono gli orbitali s.
Le funzioni d'onda Ψ(s) sono sfericamente simmetriche. La probabilità di trovare l'elettrone è la stessa in tutte le direzioni, variando solo con la distanza dal nucleo.
La rappresentazione di un'orbitale può essere fatta in modi diversi. Possiamo vederli esemplificati utilizzando una funzione orbitale particolarmente semplice, quella che descrive l'orbitale s del primo livello energetico (orbitale 1s) dell'atomo di Idrogeno.
Il modo più diretto di rappresentare un'orbitale è di tracciare la funzione orbitalica Y in dipendenza dal raggio. Per l'orbitale 1s dell'atomo di idrogeno essa vale
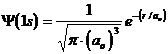
Si osserva facilmente che per r 0 il valore della funzione tende a ![]() , mentre per r la funzione tende a zero. Il suo
valore decresce dunque in modo esponenziale man mano che ci allontaniamo dal
nucleo. L'orbitale 1s è infinitamente
esteso (tutti gli orbitali lo sono).
, mentre per r la funzione tende a zero. Il suo
valore decresce dunque in modo esponenziale man mano che ci allontaniamo dal
nucleo. L'orbitale 1s è infinitamente
esteso (tutti gli orbitali lo sono).

Poiché tuttavia la funzione
orbitalica Y non presenta un significato fisico diretto
si preferisce rappresentare l'orbitale
riportando l'andamento della funzione
densità di probabilità Y Si
osserva facilmente che, per l'orbitale 1s, essa presenta lo stesso andamento
della funzione orbitalica. La probabilità Y di trovare
l'elettrone nell'unità di volume è massima e pari a ![]() in corrispondenza del nucleo (r = 0), mentre diminuisce
progressivamente allontanandoci da esso (r
in corrispondenza del nucleo (r = 0), mentre diminuisce
progressivamente allontanandoci da esso (r
L'andamento di tale funzione viene spesso rappresentato in tre dimensioni attraverso la cosiddetta nuvola di carica o nuvola elettronica. Idealmente si può immaginare di osservare l'elettrone ad intervalli di tempo regolari e di riportare le sue posizioni come punti intorno al nucleo. Si ottiene una nebbia di punti che sfuma radialmente, detta appunto nuvola elettronica. Essa rappresenta una mappatura della funzione Y . Nelle regioni dove la nuvola è più concentrata e la densità di punti è maggiore, risulta anche maggiore la probabilità di trovarvi l'elettrone.La probabilità Y di trovare l'elettrone nell'unità di volume è massima in corrispondenza del nucleo (r = 0), mentre diminuisce progressivamente allontanandoci da esso (r ). Ma in realtà il massimo di densità di probabilità non implica il massimo di probabilità.
Possiamo rendercene conto ricorrendo alla funzione di distribuzione radiale della probabilità, un modo alternativo di rappresentazione dell'orbitale che presenta il pregio di descriverlo in modo più intuitivo. Dividiamo lo spazio intorno al nucleo in gusci sferici concentrici di spessore infinitesimo dr. Il volume di un generico guscio di superficie 4pr2, che si trovi a distanza r, sarà pari a 4pr2dr e la probabilità di trovarvi l'elettrone si otterrà ovviamente come prodotto della probabilità di trovare l'elettrone nell'unità di volume Y ed il volume del guscio stesso.
dP = Ψ2 4πr2dr.
Il rapporto dP/dr rappresenta la variazione della probabilità al variare della distanza dal nucleo ed è quindi una funzione di distribuzione della probabilità in funzione del raggio (radiale)
dP/dr = Ψ2 4πr2
Tale funzione vale zero in corrispondenza del nucleo (r = 0) in quanto un punto possiede volume nullo, presenta un massimo in corrispondenza di ao (che per l'atomo di Idrogeno è pari 0.53Å e corrisponde al raggio della prima orbita di Bohr) e si annulla all'infinito.
Se sommiamo le probabilità di trovare l'elettrone in ciascun guscio fino ad una certa distanza r, otteniamo la probabilità totale di trovare l'elettrone nel volume compreso tra 0 ed r. (ciò equivale a calcolare l'integrale della funzione da 0 ad r). Tale probabilità complessiva è pari all'area sottesa dalla curva di distribuzione della probabilità. Poiché la funzione si annulla all'infinito, per ottenere una probabilità del 100% è necessario considerare un volume infinitamente grande intorno al nucleo.

Se tuttavia ci accontentiamo di una probabilità inferiore, ad esempio del 95% o del 98%, possiamo individuare una superficie tale che la probabilità di trovarvi l'elettrone all'interno sia quella desiderata ed assumere il volume così individuato come rappresentativo dell'orbitale in questione. Tale superficie, detta superficie di contorno (boundary surface) o superficie di inviluppo o superficie limite, è sferica per gli orbitali s.

Anche l'orbitale 2s (orbitale s del secondo livello energetico) è sfericamente simmetrico, ma ad una certa distanza dal nucleo la funzione d'onda Ψ si annulla e da positiva diventa negativa (nodo). All'interno della superficie di controrno è pertanto presente una superficie nodale che separa la regione interna in cui la funzione d'onda è positiva dalla regione più esterna in cui la funzione d'onda è negativa. La superficie nodale, a probabilità nulla, separa due massimi, uno più vicino al nucleo ed un massimo principale più lontano.

Per l'orbitale 3s la funzione di distribuzione radiale di probabilità presenta tre massimi (due secondari e un massimo principale) e due punti nodali. La superficie di inviluppo contiene quindi due superfici nodali.

Gli orbitali ns dei livelli superiori mantengono la simmetria sferica e presentano n massimi di densità elettronica ed n-1 superfici nodali (con n = livello energetico di appartenenza).

Gli orbitali p hanno simmetria cilindrica, possiedono cioè un asse preferenziale e non cambiano segno per rotazione attorno ad esso. Sono costituiti da due lobi ad elevata densità elettronica (in cui la funzione d'onda Ψ assume segno opposto) ed un piano nodale nell'origine (nucleo). Spesso le superfici di contorno vengono rappresentate con un colore diverso per i due lobi ad indicare il diverso segno (positivo e negativo) della funzione d'onda.

Gli orbitali p sono tre per livello energetico (tranne il primo livello energetico) ed essendo orientati uno perpendicolarmente all'altro nella direzione dei tre assi cartesiani, vengono indicati con la notazione: px, py, pz.

Gli orbitali 2p presentano un piano nodale passante per il nucleo che separa due lobi in cui la funzione d'onda Ψ presenta segni opposti senza alcuna altra superficie nodale al loro interno.

Gli orbitali 3p presentano un piano nodale passante per il nucleo che separa due lobi ad elevata densità elettronica. Ciascun lobo è diviso da una superficie nodale in due regioni in cui la funzione d'onda Ψ presenta segni opposti. La superficie nodale, a probabilità nulla, suddivide ciascun lobo in due massimi di probabilità, uno secondario più vicino al nucleo ed uno principale più lontano.

Gli orbitali 4p presentano ciascun lobo suddiviso in 3 regioni (in cui la funzione d'onda Ψ presenta segni alternativamente opposti) da due superfici nodali.

Gli orbitali np dei livelli superiori mantengono la simmetria cilindrica e presentano ciascun lobo suddiviso in n-1 regioni a massima densità elettronica separate da n-2 superfici nodali (con n = livello energetico di appartenenza).
Gli orbitali d sono 5 per livello energetico (tranne i primi due livelli energetici). Quattro di essi sono tetralobati con i 4 lobi in cui la funzione d'onda Ψ assume segno alternativamente opposto. Il quinto orbitale d è bilobato con una regione anulare (in cui la funzione d'onda ssume segno opposto) ad alta densità elettronica che circonda il nucleo.

Gli orbitali d tetralobali presentano due piani nodali. Ad esempio l'orbitale dxy presenta due piani nodali perpendicolari che si intersecano sull'asse z

Gli orbitali f sono 7 per livello energetico (tranne i primi tre livelli energetici).

Il significato generale dei numeri quantici n, l ed m rimane inalterato anche se è necessario fare le seguenti precisazioni:
a) Il valore assunto da 'n' determina l'energia dell'orbitale ed individua i 7 livelli energetici possibili, detti anche strati o gusci.
b) il valore assunto da 'l' è associabile al tipo ed alla forma dell'orbitale. Esistono 4 tipi di orbitali. Gli orbitali 's' presentano simmetria sferica, gli orbitali 'p' presentano una forma a otto di rotazione, gli orbitali 'd' ed 'f' forme complesse.
c) il valore assunto da 'm' è associabile al numero di orbitali per tipo presenti in ciascun livello energetico.
d) Naturalmente anche il modello di Schrödinger prevede l'esistenza del quarto numero quantico di spin e non possono essere presenti più di due elettroni per orbitale
1° Livello energetico
1 orbitale s (1s) capienza max: 2 elettroni
2° Livello energetico
1 orbitale s (2s) capienza max: 2 elettroni
3 orbitali p (2p) capienza max: 6 elettroni
3° Livello energetico
1 orbitale s (3s) capienza max: 2 elettroni
3 orbitali p (3p) capienza max: 6 elettroni
5 orbitali d (3d) capienza max: 10 elettroni
4° Livello energetico
1 orbitale s (4s) capienza max: 2 elettroni
3 orbitali p (4p) capienza max: 6 elettroni
5 orbitali d (4d) capienza max: 10 elettroni
7 orbitali f (4f) capienza max: 14 elettroni
I livelli successivi presentano al massimo la struttura orbitalica del quarto livello. Gli atomi più pesanti, come l'Uranio, hanno elettroni a sufficienza per occupare 7 livelli energetici, senza tuttavia riuscire a riempirli completamente.
Anche se, in teoria, i livelli energetici più esterni possono presentare tutti i tipi di orbitali, in pratica un atomo non possiede mai un numero di elettroni sufficiente a riempire tutti i possibili orbitali esterni. Così la struttura orbitalica di un atomo è, in pratica, la seguente
|
Livello |
Orbitali consentiti |
Campienza elettronica |
|||
|
|
1s |
|
|
|
|
|
|
2s |
2p |
|
|
|
|
|
3s |
3p |
3d |
|
|
|
|
4s |
4p |
4d |
4f |
|
|
|
5s |
5p |
5d |
5f |
|
|
|
6s |
6p |
6d |
|
|
|
|
7s |
|
|
|
|
I tre orbitali p di un medesimo livello energetico presentano lo stesso contenuto energetico e si dicono pertanto isoenergetici o degeneri. Questo accade anche per i cinque orbitali d di un medesimo livello energetico e per i sette orbitali f di un medesimo livello energetico.
 |
|
| Appunti Ingegneria tecnico |  |
| Tesine Geografia |  |
| Lezioni Biologia |  |