 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 6546 | Gradito: |
Leggi anche appunti:Le sostanzeLE SOSTANZE 1. LE SOSTANZE PURE I metodi per separare i componenti Il CarbonioIl Carbonio Carbonio Elemento chimico di simbolo C e numero atomico 6, appartenente Repulsione di van der Waals a corto raggio e potenziale di Lennard-JonesRepulsione di van der Waals a corto raggio e potenziale di Lennard-Jones In |
 |
 |
Un elettrolita anfotero o anfolita è un elettrolita che può comportarsi sia come acido (cedendo protoni) che come base (acquistando protoni). Il suo comportamento risulta quindi analogo a quello di un sale formato da un acido debole ed una base debole (vedi paragrafo precedente).
Consideriamo ad esempio una soluzione di Idrogeno Carbonato di Sodio NaHCO3 di concentrazione C = 10-2 M. In soluzione è completamente dissociato in C ioni Na+ e C ioni HCO3-. L'acido carbonico H2CO3, essendo un acido debole biprotico, presenta due costanti di dissociazione pari a ka1 = 4.3 10-7 e ka2 = 5.6 10-11.
NaHCO3 → Na+ + HCO3-
-C +C +C
L'anione bicarbonato HCO3- in soluzione si comporta sia come un acido, dando l'equilibrio di seconda dissociazione, con ka2 = 5.6 10-11
HCO3- ![]() H+ + CO32-
H+ + CO32-
sia come una base, dando idrolisi basica, con kh = kw/ ka1 = 10-14/4.3 10-7= 2.36 10-8 (come abbiamo visto in precedenza la reazione può anche essere considerata una reazione acido-base con HCO3- che rappresenta la base coniugata (kbc = kw/ ka1 = 10-14/4.3 10-7= 2.36 10-8) dell'acido carbonico)
HCO3- + H2O ![]() H2CO3 + OH-
H2CO3 + OH-
Per calcolare il pH di tale soluzione sarebbe necessario tener conto simultaneamente dei precedenti due equilibri e dell'equilibrio di dissociazione dell'acqua.
Poiché la costante di seconda dissociazione dell'acido carbonico (ka2 = 5.6 10-11) è inferiore alla sua costante di idrolisi (kh = kw/ ka1 = 2.36 10-8) possiamo prevedere che l'anione bicarbonato si riassoci in percentuale maggiore (idrolisi basica) rispetto a quanto si dissoci (dissociazione acida). La soluzione sarà pertanto basica.
La soluzione esatta del problema richiederebbe naturalmente la risoluzione di un sistema di equazioni in cui compaiano tutte le condizioni relative ai tre equilibri.
|
Soluzione esatta Nei tre equilibri compaiono le seguenti 5 incognite. 1) [H+] 2) [OH-] 3) [H2CO3] 4) [HCO3-] 5) [CO32-] Dobbiamo pertanto scrivere 5 equazioni indipendenti nelle 5 incognite. Le prime tre equazione si ricavano dalle equazioni di equilibrio rispettivamente di prima e seconda dissociazione dell'acido e di dissociazione dell'acqua 1) la quarta si ottiene dal bilancio delle cariche (la somma di tutte le cariche positive deve essere uguale alla somma di tutte le cariche negative)
e, ricordando che il sale è completamente dissociato e quindi che [Na+] = C la quinta si ricava infine dal bilancio di massa. utilizzando le 5 equazioni ed effettuando le opportune sostituzioni in funzione della concentrazione di ioni H+ si ottiene
con x = [H+] un'equazione di quarto grado che ci permette di calcolare il valore esatto della concentrazione totale di ioni H+ per una soluzione di un anfolita. |
Per un calcolo approssimato sottraiamo membro a membro il bilancio di carica ed il bilancio di massa, ottenendo
![]()
dalla 1) esplicitiamo la concentrazione dell'acido indissociato H2CO3 e sostituiamola nella 5)
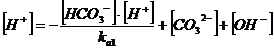
dalla 2) ricaviamo la concentrazione dell'anione carbonato CO32- e sostituiamola nella 6)
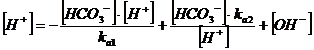
dal prodotto ionico dell'acqua ricaviamo la concentrazione degli ioni OH- e sostituiamo nella 7)

Se ora assumiamo che, sia l'equilibrio di idrolisi che quello di dissociazione acida, avendo in genere costanti piccole, siano molto spostati verso sinistra, la concentrazione di HCO3- sarà prevalente rispetto a quelle di CO32- e H2CO3
[HCO3-] >> [CO32-] + [H2CO3]
e quindi
[HCO3-] + [CO32-] + [H2CO3] ≈ [HCO3-]
ciò significa che la concentrazione di equilibrio di HCO3- è praticamente uguale alla sua concentrazione iniziale. Dal bilancio di massa si avrà infatti
![]()
che, sostituita nella 7), ci dà
![]()
![]()
8) 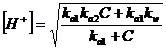
Sostituendo i valori otteniamo
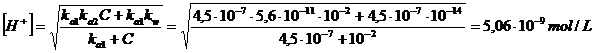
La 8) può essere ulteriormente semplificata, dividendo numeratore e denominatore per C otteniamo
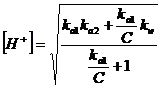
se ora, come spesso avviene, sono verificate le seguenti condizioni
C >> ka1 e ![]()
e quindi
![]() e
e ![]()
la 9) diventa
![]()
Eseguendo il logaritmo decimale negativo di entrambi i membri si ha
pH = ½ (pka1 + pka2)
La 10) equivale a prendere in considerazione il seguente equilibrio, in cui si assume che l'equilibrio di seconda dissociazione dell'acido sia sincronizzato con l'equilibrio di idrolisi
HCO3- + HCO3- ![]() H2CO3 + CO32-
H2CO3 + CO32-
C - x C - x x x
In altre parole, per ogni ione HCO3- che si dissocia in CO32- e H+, un altro ione HCO3- si riassocia con uno ione H+ per dare . H2CO3
Come si può osservare, nell'approssimazione considerata si assume che all'equilibrio sia
[H2CO3] = [CO32-]
ora esplicitiamo la concentrazione di HCO3- dalla relazione di equilibrio della prima dissociazione acida
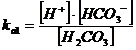 →
→ ![]()
e lo sostituiamo nella relazione di equilibrio della seconda dissociazione acida
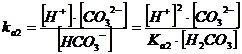
ricordando infine che [H2CO3] = [CO32-], otteniamo
![]()
e quindi
![]() mol/L
mol/L
che corrisponde ad un pH = 8.31 (basico).
Si noti come, anche in questo caso come nel paragrafo precedente, la concentrazione degli ioni H+, e quindi anche il pH, risulti indipendente (almeno nell'approssimazione che stiamo considerando) dalla concentrazione C del sale.
Si noti infine che la formula semplificata per il calcolo del pH di una soluzione contenente un elettrolita anfotero è analoga a quella trovata nel paragrafo precedente per un sale formato da un acido debole ed una base debole.
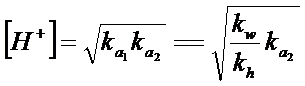
con
ka1 = costante di prima dissociazione acida
ka2 = costante di seconda dissociazione acida
kh = costante di idrolisi
Se il sale deriva da un acido debole triprotico H3A (ad esempio l'acido fosforico H3PO4), le formule per il calcolo del pH saranno
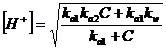 oppure
oppure ![]()
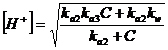 oppure
oppure ![]()
 |
| Appunti su: calcolo ph acidi anfoliti, 616E666F6C697461, https:wwwappuntimaniacomscientifichechimicaidrolisi-di-elettroliti-anfote73php, anfoliti, anfolita, |
|
| Appunti Ingegneria tecnico |  |
| Tesine Biologia |  |
| Lezioni Geografia |  |