 |
|
| Appunti tecniche |
|
 |
|
| Appunti tecniche |
|
| Visite: 956 | Gradito: |
Leggi anche appunti:Preamplificatore non reazionatoPreamplificatore non reazionato · Premesse DiodoDIODO Componente di un circuito elettrico che permette il passaggio Motori endotermici alternativiMotori endotermici alternativi Caratteristiche: - Sono |
 |
 |
Stabilità delle reazioni
In generale, dato un sistema che presenta una funzione di trasferimento F(s), dove s=s+jw, condizione necessaria affinché il sistema sia stabile è che i poli di F(s) non compaiono nel semipiano positivo (zero compreso) delle s (fig 1).
Limitando il
discorso agli amplificatori, vediamo ora un criterio per determinare la
loro stabilità.

Il sistema che prendiamo in analisi presenta dunque un anello di reazione e una funzione di trasferimento con questa forma:
![]()
Facciamo l'ipotesi che i blocchi G e H siano in partenza stabili, in altre parole non abbiano poli per s
Questo significa che neanche il denominatore di GF
![]()
presenta dei poli.
Immaginando di scomporre M(s) in numeratore N(s) e denominatore D(s), abbiamo che, per le ipotesi fatte, D(s) non presenta poli per s 0. Quindi non resta che stabilire se N(s) presenta degli zeri, oppure, equivalentemente, se M(s) presenta degli zeri.
In conclusione si ha stabilità quando 1+GH non presenta zeri (né poli per ipotesi) per s
Per determinare il numero e la posizione dei poli possiamo utilizzare un risultato della teoria delle funzioni analitiche che mette in relazione il comportamento di F(s) con il numero dei suoi zeri e dei suoi poli.
poli zeri
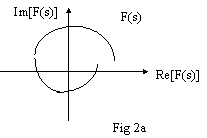

Con riferimento alle fig. 2a e 2b, la
quantità ![]() è uguale al numero di inviluppi di F(s) intorno all'origine
(il verso di rotazione dipende da quale delle due quantità è maggiore). Se il
dominio D scelto non comprende poli e zeri, oppure se il numero dei poli è
uguale al numero degli zeri, F(s) non inviluppa l'origine (inviluppare l'origine=compiere un giro completo intorno
all'origine).
è uguale al numero di inviluppi di F(s) intorno all'origine
(il verso di rotazione dipende da quale delle due quantità è maggiore). Se il
dominio D scelto non comprende poli e zeri, oppure se il numero dei poli è
uguale al numero degli zeri, F(s) non inviluppa l'origine (inviluppare l'origine=compiere un giro completo intorno
all'origine).
Per le considerazioni precedenti, sappiamo che la nostra F(s) non presenta poli per s 0; di conseguenza, qualunque contorno contenuto nel semipiano s 0 noi consideriamo, la nostra F(s) non dovrebbe inviluppare l'origine. Se ciò accade significa che esiste almeno uno zero nel semipiano s 0 e quindi il sistema è instabile. Il contorno più grande che possiamo considerare è quello che contiene tutto il semipiano s 0, quindi:
![]()
In definitiva, noi dobbiamo studiare la quantità 1+G(s)H(s) nell'intorno dell'origine; se questa funzione contorna l'origine il sistema è instabile, altrimenti è stabile.
Equivalentemente, ed è quello che faremo, possiamo studiare la funzione G(s)H(s) nell'intorno di 1. Inoltre, siccome G(s)H(s) è a coefficienti reali, è simmetrica rispetto all'asse reale, quindi possiamo limitare lo studio all'intervallo [0,+
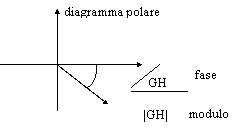
Per fare questo utilizziamo un diagramma polare (fig 3b), su cui disegniamo, al variare di jw da 0 a + , il modulo e la fase di GH.
Fig 3b

In figura 3a compaiono due forme tipiche di GH(jw) per gli amplificatori. Vediamo che la curva che passa tra 0 e 1 (non contorna l'1) indica un sistema stabile, mentre la curva che passa oltre l'1 indica un sistema instabile.
Il criterio che abbiamo visto è teorico. Nella pratica occorre avere un margine maggiore per decidere se un sistema è stabile oppure no.
Consideriamo la
fase di GH quando |GH|=1; nell'esempio di
fig 4, la curva che passa internamente a 1 interseca la circonferenza di
raggio 1 nel punto A, e qui la fase a vale circa 225°; la curva che passa esternamente a 1 interseca la
circonferenza nel punto B, e qui la fase a vale circa 135°.
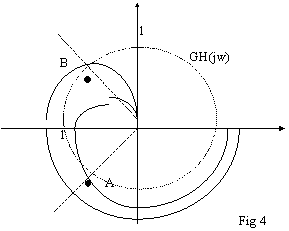
Definizione: Margine di fase = fase di GH (quando |GH|=1) - 180°
Nell'esempio il margine di fase della prima curva è 225°-180°=45°, il margine di fase della seconda curva è 135°-180°=-45°.
Il criterio teorico, tradotto secondo il margine di fase, dice:
se margine di fase > 0 T sistema stabile
se margine di fase < 0 T sistema instabile
Il criterio pratico dice:
se margine di fase T sistema "ingegneristicamente" stabile
se margine di fase < 45° T sistema "ingegneristicamente" instabile
Definizione: Margine di guadagno (in dB) = |GH| quando fase di GH=180°
Nell'esempio, quando la fase è 180°, la prima curva ha modulo <1, quindi il margine di guadagno è >0, la seconda ha modulo >1, quindi il margine di guadagno è <0.
Il criterio teorico, tradotto secondo il margine di guadagno, dice:
se margine di guadagno > 0 T sistema stabile
se margine di guadagno < 0 T sistema instabile
Il criterio di Bode discende da quello di Nyquist ma è più semplicistico. Nonostante questo, per noi va benissimo, perché limitiamo il nostro studio agli amplificatori.
-90° Fig 4b Fig 4a

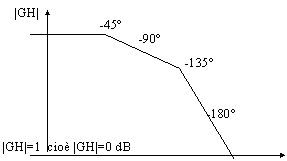
Esiste una precisa corrispondenza tra il grafico di fig 4a e quello di fig. 4b. A destra abbiamo il comportamento modulo/fase di GH al variare di jw, tracciato su un diagramma polare, a sinistra abbiamo il comportamento del modulo di GH, tracciato su un diagramma di Bode. Al diminuire della fase (da -45° a -180°) il modulo diminuisce fino a diventare minore di 1: questo accade a destra quando la curva interseca la circonferenza unitaria, a sinistra quando la curva passa al di sotto dell'asse X (0 dB).
Il criterio di Nyquist ci dice che una curva di questo tipo (fig 4b) indica instabilità del sistema. A sinistra (fig 4a) osserviamo che la curva taglie l'asse X con una pendenza di -40dB/decade.
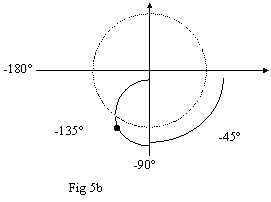

In questo secondo caso il criterio di Nyquist ci dice che il sistema è stabile, perché la curva non contorna l'1. In fig 5a osserviamo che la curva taglia l'asse X (cioè |GH| diventa minore di 1, o minore di 0dB) quando la sua pendenza è pari a -20dB/decade. In fig. 5b notiamo che la curva taglia la circonferenza unitaria con un margine di fase maggiore di 45°, viene quindi rispettato la condizione "pratica" di stabilità.
Da queste considerazioni si può dedurre che la curva del modulo di GH non deve tagliare l'asse X con un'inclinazione superiore a -20 dB/decade, altrimenti il sistema è (praticamente) instabile. Il caso estremo si ha quando il margine di fase è proprio 45°, cioè quando la curva a destra taglia la circonferenza unitaria proprio a -135° (cioè a 225°). Questo caso è rappresentato dai grafici di fig 6 a e 6b; a sinistra abbiamo che l'inclinazione della curva cambia proprio nel punto di intersezione con l'asse X.

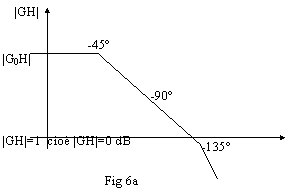
Chiamando a il polo a sinistra e b il polo a destra, quando si verifica questa condizione abbiamo che la seguente relazione è vera:
![]()
Infatti il segmento di curva che unisce i due poli ha un'inclinazione di -20dB/decade, cioè è inclinata di 45 gradi, quindi la distanza che separa i due poli sull'asse X è pari alla distanza che li separa sull'asse Y, distanza pari a G0H.
Abbiamo visto in precedenza che quando questa relazione è soddisfatta il sistema presenta i seguenti valori:
Q=1, k=1/2 e w a
Consideriamo uno dei quattro amplificatori, per esempio l'amplificatore di tensione, rappresentato in fig. 7.
Come sappiamo,
per calcolare il guadagno di anello dobbiamo eliminare il generatore
esterno ed esprimere vi in funzione di (a seconda di quale definizione di Ga
si utilizza)
![]() :
:
![]()
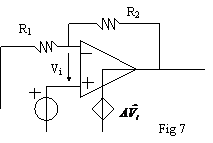
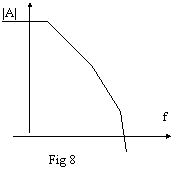
La curva di risposta in frequenza di un amplificatore operazionale ha il tipico andamento raffigurato in fig. 8.
Questo è
l'andamento tipico della curva di risposta di un amplificatore operazionale
non compensato; essa presenta 3
poli naturali. Ora vogliamo
disegnare la curva di risposta dell'amplificatore di tensione, considerando
quindi l'effetto della reazione. In altre parole vogliamo disegnare
l'andamento di |Ga|.
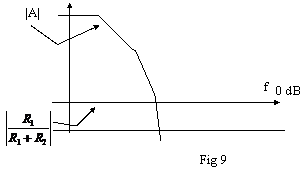
Guardando la formula che ci fornisce Ga, possiamo vedere che
l'andamento di |Ga| è graficamente pari alla somma degli andamenti
di |A| e di  . In fig 9 sono rappresentati separatamente i grafici
relativi a queste due quantità.
. In fig 9 sono rappresentati separatamente i grafici
relativi a queste due quantità.
Nota che:
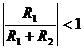 , quindi la retta oizzontale che rappresenta questa
quantità rimane sotto l'asse a 0 dB.
, quindi la retta oizzontale che rappresenta questa
quantità rimane sotto l'asse a 0 dB.
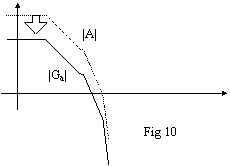
Sommando i due
grafici otteniamo il grafico di fig 10, che è uguale al grafico di |A|
ribassato di una quantità pari al partitore delle resistenze. Se il
partitore valesse 1 (=0dB), non ci sarebbe nessuna modifica all'andamento;
più il partitore ha un valore vicino a zero, maggiore è l'abbassamento. Se
l'abbassamento è sufficientemente grande, il sistema diventa stabile,
perché la curva taglia l'asse 0dB con un'inclinazione di -20dB/decade; se
l'abbassamento è insufficiente, il sistema è instabile. |G a|
Un modo per stabilizzare l'anello è quello del polo dominante. In generale occorre inserire un blocco di compensazione C all'interno dell'anello di reazione (fig 11)

Come
rappresentato in fig 12, si tratta di inserire un polo ad una frequenza
molto bassa, in modo da ridurre la pendenza della curva. f1 : primo polo naturale fc : polo di compensazione In questo modo
la curva taglia l'asse 0dB con una pendenza di -20dB/decade e il sistema è
stabile.
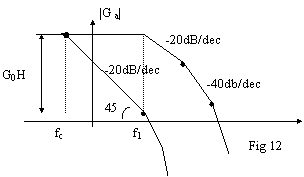
Nota che vale la seguente relazione:
![]()
Infatti, visto che un'inclinazione di 20dB/decade significa un'inclinazione di 45°, la distanza che separa i due poli è pari all'altezza massima della curva.
Inserendo il polo di compensazione otteniamo un sistema con 4 poli, ma i due poli naturali più a destra si trovano molto sotto all'asse 0 dB e quindi sono trascurabili (ricorda che a 0dB il guadagno è pari a 1).
Riassumendo: l'abbassamento dovuto al partitore e il polo di compensazione sono due fattori concomitanti che portano il sistema alla stabilità. Se l'abbassamento è grande, il polo di compensazione può essere messo a una frequenza più grande; se l'abbassamento è piccolo, al limite nullo, il polo di compensazione deve essere messo a una frequenza molto bassa.
La curva dell'amplificatore compensato risultante è rappresentata in fig 13.
Indicativamente,
il polo di compensazione cade a una frequenza intorno a 1 Hz, mentre il
polo naturale si trova generalmente intorno ai 50-100 kHz. Per inserire il
polo di compensazione occorre mettere un condensatore in parallelo al segnale;
negli amplificatori operazionali il condensatore utilizzato ha un valore di
circa 10 pF sfrutta l'effetto Miller
(vedi su slide il valore C0).
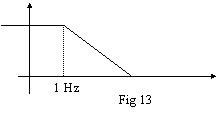
Un polo a così bassa frequenza apparentemente non comporta nessun problema. In realtà il guadagno di anello inizia ad abbassarsi già a basse frequenze, e tutti vantaggi legati all'avere un alto guadagno subiscono una diminuzione: il comportamento dell'anello non è più efficace come prima (insensibilità ai rumori, valore preciso nel guadagno di anello).
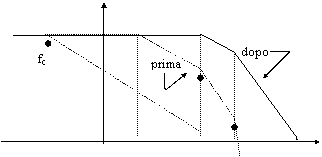
Un'altra soluzione consiste nell'introduzione di una coppia polo-zero. Immaginiamo di avere un sistema instabile avente la curva di risposta rappresentata in fig. 14.
Sul grafico
compare anche l'eventuale polo di compensazione, ad una frequenza molto bassa. Proviamo ora ad
inserire uno zero alla stessa frequenza del primo polo naturale (quello a
frequenza minore), annullo quel polo e la curva si modifica come descritto
in fig. 15.

|Ga|
Otteniamo una
curva traslata a destra, dove quello
che era il secondo polo è diventato il primo polo. Se a questo punto
vogliamo inserire il polo di compensazione, possiamo metterlo più a destra
rispetto alla situazione precedente, in modo che il guadagno rimanga alto
per un campo di frequenze più ampio. Fig 15
![]()
Abbiamo già visto in precedenza che per piazzare una coppia polo-zero occorre inserire in parallelo al segnale una coppia resistenza - condensatore; la posizione dello zero dipende dai valori di R e C, quindi posso piazzare lo zero con grande precisione.
Quelle che abbiamo visto sono le uniche due tecniche applicate agli amplificatori operazionali.
Consideriamo il circuito integratore di
fig. 16 e calcoliamo il guadagno di anello Ga con la solita
procedura:

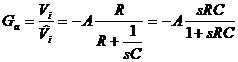
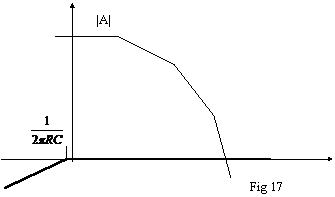
Disegniamo sul diagramma di Bode il grafico
dell'andamento di |A| (classica curva a tre poli dell'amplificatore
operazionale) e dell'andamento di ![]() (fig. 17).
(fig. 17).
La curva a
tratto sottile rappresenta l'andamento di |A|, mentre la curva a tratto
spesso rappresenta l'andamento di Come si può
vedere, quando s , la seconda curva tende a 0dB (cioè a 1). Se adesso
sommiamo graficamente le due curve, otteniamo il grafico di fig. 18.
![]() .
.
Si vede
chiaramente (criterio di Bode) che il sistema è instabile. Se applichiamo
ora il metodo del polo dominante, otteniamo il risultato presentato in fig.
1
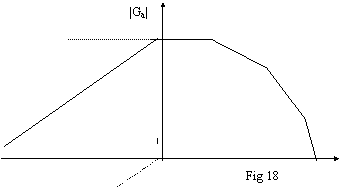
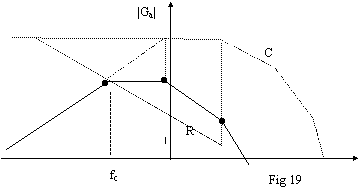
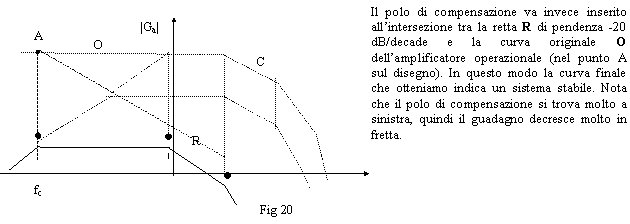
Nonostante
l'introduzione del polo di compensazione, il sistema è ancora instabile.
Infatti, in questo caso, il punto da prendere come polo di compensazione
non è l'intersezione tra la curva di
risposta C e la retta R con pendenza 20dB/decade che parte dal primo polo naturale.
![]()
Consideriamo il
circuito derivatore di fig 21 e immaginiamo che l'amplificatore
operazionale impiegato sia compensato internamente (quindi ha un polo
dominante). Calcoliamo il
guadagno di anello: Disegniamo
separatamente la curva di |A| e di Questa curva
indica un sistema instabile. Una regola
pratica da seguire è la seguente: l'amplificatore
operazionale compensato internamente va bene se la rete in cui è inserito è
solo passiva. In caso contrario bisogna
mettere un amplificatore da compensare e lo adatto alla rete.
![]()
![]() (fig 22). Componendo i due grafici otteniamo la curva di
fig 23.
(fig 22). Componendo i due grafici otteniamo la curva di
fig 23.

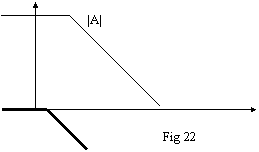
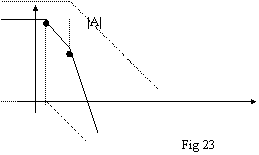
Prendiamo in
esame il circuito di fig 24. L'idea (sbagliata) è quella di inserire un
condensatore con l'intenzione di eliminare un po' di rumore sull'uscita. Nota:
l'amplificatore operaz. In questione è compensato internamente. In questo caso
teniamo conto anche di Ro che, anche se piccola, fa sentire la
sua influenza. Calcoliamo
dunque Ga:

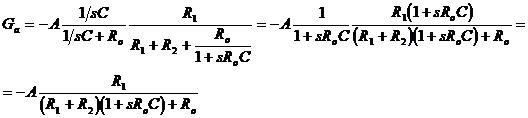
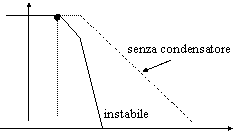
Il guadagno di anello presenta un polo, quindi la curva del sistema (che senza condensatore è stabile) si trasforma nel modo descritto in fig. 25.
Con
l'introduzione del nuovo polo, dovuto alla presenza del condensatore, il
sistema diventa instabile. polo introdotto Fig 25
Quando un sistema non è stabile, lo si chiama generalmente "sistema oscillante", ma qual è la causa di tale oscillazione? La rotazione di fase introdotta nell'anello (dovuta a poli e zeri) può modificare il verso della reazione; in particolare, se la rotazione è di 180°, la reazione cambia di segno ad ogni ciclo (da positiva diventa negativa e viceversa).
Esisterà una frequenza particolare alla quale la rotazione di fase è tale da invertire il verso della reazione; se il guadagno di anello è maggiore di 1, a quella frequenza l'uscita aumenta (in modulo) ad ogni giro; se invece il guadagno è uguale a 1, l'ampiezza del segnale non viene modificata mentre il verso si inverte ad ogni giro. Siccome questo fenomeno avviene ad una sola e ben precisa frequenza, in ingresso e in uscita devo una sinusoide.
Le condizioni alle quali avviene questo fenomeno sono dette condizioni di Barkhausen:
rotazione di fase complessiva = 0
modulo del guadagno di anello = 1
Se il guadagno è maggiore di 1, la
sinusoide in uscita avrà un'ampiezza crescente. Ma siccome la dinamica non
è infinita (fig 26), la tensione di uscita Vu non può crescere
all'infinito. Ad un certo punto il sistema esce dalla
zona di linearità e si ottiene un'oscillazione "sporca" (fig 27).

Per ottenere un'oscillazione "pulita" devo
fare in modo che il sistema rimanga in linearità.

Fig 27
Ma il problema è un altro; abbiamo visto che per attivare l'oscillazione occorre avere una precisa frequenza che soddisfi le condizioni di Barkhausen; ma questo significa avere in ingresso una sinusoide pulita, che è quella che non abbiamo e che vogliamo ottenere in uscita.
Nei circuiti reali c'è sempre del rumore, composto da un gradissimo numero di frequenze, e tra queste ci saraà quella particolare frequenza che innesca l'ocillazione. Però inizialmente il guadagno dovrà essere maggiore di 1, in modo da raggiungere una certa ampiezza; una volta che la sinusoide si è creata, occorre rimettere il guadagno a 1, in modo da stabilizzare la reazione e fissare l'ampiezza della sinusoide. Questa operazione di controllo è svolta da un circuito che si chiama appunto: circuito di controllo dell'ampiezza.
 |
| Appunti su: |
|
| Appunti costruzione |  |
| Tesine Gestione |  |
| Lezioni Ingegneria tecnico |  |