 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1961 | Gradito: |
Leggi anche appunti:Funzioni a due variabiliFUNZIONI A DUE VARIABILI DEFINIZIONE Una funzione reale di due variabili La forza di LorentzLa forza di Lorentz La forza di Lorentz è una forza originata dal campo Le geometrie non euclideeLe geometrie non euclidee Il problema delle geometrie non euclidee e la rivoluzione |
 |
 |
LE TASSELLAZIONI regolari
Una tassellazione
regolare è un ricoprimento del piano con poligoni regolari in modo che ad ogni
vertice venga a contatto lo stesso numero di poligoni. Le tassellazioni del
piano euclideo sono: nella quale per ogni vertice si incontrano 6
triangoli equilateri; nella quale per ogni vertice si incontrano 4
quadrati; e nella quale per ogni vertice si incontrano tre esagoni.La
notazione è denominata un simbolo di Schläfli e
significa che ci sono q poligoni regolari di p lati che si
incontrano per ogni vertice.
Esistono molte tassellazioni regolari del piano iperbolico.
E' possibile determinare se è una tassellazione del piano
euclideo, del piano iperbolico, o del piano ellittico guardando la somma 1/N
+ 1/K .
Se la somma è uguale 1/2, come accade per le tre tassellazioni citate precedentemente, allora è una tassellazione euclidea.
Se la somma è minore di 1/2, allora la
tassellazione è iperbolica.
- Se la somma è maggiore di 1/2,
allora la tassellazione è ellittica.
Ci si potrebbe chiedere perché per un tassellazione , ci sono K poligoni regolari di N lati ad ogni vertice.
Così l'angolo ad ogni vertice è 360°/K.
Poiché un poligono
regolare di N lati ha N angoli uguali, ciascuno di 360°/K
, allora la somma degli angoli di un poligono è N 360°/K .
Ora, nel piano euclideo un triangolo ha esattamente la somma degli angoli
interni pari a 180°; nel piano iperbolico minore; e nel piano ellittico
maggiore.
Dividendo un
poligono in triangoli si può immediatamente vedere che la somma degli angoli di
un poligono regolare di N lati è esattamente pari a (N -
2)180° nel piano euclideo; minore in quello iperbolico; maggiore in quello
ellittico. Di conseguenza, se N 360°/K è uguale a (N
- 2)180°, allora
può soltanto essere euclidea; se è minore, iperbolica; e se
è maggiore, ellittica.
N 360°/K
= (N - 2)180° dividiamo per 360°
N/K = (N - 2)/2
N/K = N/2 - 1 moltiplichiamo per 1/N
1/K = 1/2 - 1/N
ovvero 1/N + 1/K = 1/2
Ecco perché se 1/N + 1/K è uguale 1/2, allora può soltanto essere euclideo; se minore, iperbolica; e se maggiore, ellittica.
Alcuni esempi di tassellazioni del piano iperbolico:


Tassellazione regolare del piano
iperbolico Tassellazione
del piano iperbolico
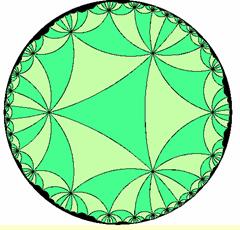

Tassellazione regolare Tassellazione regolare


Tassellazione
Tassellazione
 |
| Appunti su: |
|
| Appunti Contabilita |  |
| Tesine Fisica |  |
| Lezioni Statistica |  |