 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1523 | Gradito: |
Leggi anche appunti:UN’ABITUDINE di pensiero radicata a fondoUN’ABITUDINE di pensiero radicata a fondo Come si spiega dunque il fatto Definizione di algebra di BooleDefinizione di algebra di Boole Si dice che un insieme K è munito della struttura Le funzioni goniometriche seno e cosenoLe funzioni goniometriche seno e coseno La circonferenza goniometrica è una |
 |
 |
Le unità statistiche presentano intensità diverse dei caratteri quantitativi (e modalità diverse dei caratteri qualitativi), ad esempio la statura di 123 iscritti di leva varia tra cm 140 e cm 195; il loro perimetro toracico, tra 60 e 100 cm; il colore degli occhi e dei loro capelli muta, passando dalle tinte chiare a quelle nere; la produzione del frumento in Italia durante un dato periodo presenta notevoli differenze di anno in anno, passando da un minimo di 63,3 milioni di quintali nell'anno 1977 a un massimo di 99,9 milioni di quintali nel 1971.
È questo un fenomeno di carattere generale. Prendiamo un Annuario statistico ed apriamolo a caso: constateremo facilmente che l'ammontare della popolazione varia attraverso il tempo; che varia il numero mensile dei nati, dei matrimoni e dei morti; che, per certe malattie, si muore di più in certe stagioni che in altre; che varia nel corso dell'anno il volume dell'attività economica e, conseguentemente, quello della disoccupazione e dell'occupazione operaia, ecc.
Anche senza moltiplicare gli esempi ci si può convincere di un fatto fondamentale: in ogni campo, si ha che le intensità dei caratteri quantitativi non sono affatto costanti, e così le modalità dei caratteri qualitativi presentano sempre delle differenziazioni.
Si presenta cioè il fenomeno (che è fondamentale per la Statistica) della variabilità
Più precisamente si parla di variabilità, quando si tratta di caratteri quantitativi (con diverse intensità), di mutabilità, quando si tratta di caratteri qualitativi (con diverse modalità).
Ora, le medie, di cui abbiamo parlato precedentemente, ci danno un'idea sintetica del fenomeno studiato, ma non dicono assolutamente nulla sulla variabilità.
È quindi molto interessante trovare un modo per dare un'idea, per misurare questa variabilità.
Così, se in un'azienda il salario medio giornaliero degli operai è € 40,00, può darsi che tutti abbiano lo stesso salario di € 40,00, ovvero che ci siano divergenze più o meno notevoli. Ed è noto il detto, secondo cui, in Statistica, «se io ho due polli e tu non ne hai nessuno, è come se ne avessimo uno per ciascuno»!
Noi studieremo i principali indici elaborati dalla metodologia statistica per la misura della variabilità (ci limiteremo ai caratteri quantitativi).
Il problema della variabilità (e della sua misura) ha importanza notevole anche perché, come abbiamo detto, spesso si ricorre a rilevazioni parziali, campionarie.
Se il fenomeno in esame fosse costante, la rilevazione parziale sarebbe senz'altro sufficiente per avere dei dati globali; invece, data la variabilità, c'è il rischio che il campione considerato presenti caratteristiche diverse da quelle dell'universo.
Così, se tutti gli individui avessero la stessa statura, basterebbe misurarne uno per conoscere quella di tutti; data la variabilità delle stature, se ci si limita ad un campione non è affatto certo che la statura trovata nel campione sia la stessa che si troverebbe nell'universo; e la probabilità di commettere un errore in questa stima è tanto maggiore quanto maggiore è la variabilità.
Una prima semplice misura della variabilità è il campo di variazione (o ampiezza del campo di variazione);
esso è la differenza fra il valore massimo e il valore minimo osservati.
Se lo indichiamo con R si ha:
R =Xmax-Xmin
Così, nel caso delle stature, il campo di variazione è di cm 55, nel caso dei perimetri toracici è di cm 40, nel caso delle produzioni di frumento è di 36,6 milioni di q.
Ma evidentemente si tratta di una misura del tutto grossolana e insufficiente della variabilità, in quanto su di essa non influiscono affatto i valori intermedi.
Se, per es., la produzione del frumento fosse stata di 63,3 milioni di q nel 1977 e di 98,1 in tutti gli altri anni del periodo considerato, il campo di variazione sarebbe risultato ancora lo stesso, mentre molto diversa sarebbe stata la sostanza del fenomeno.
La variabilità si misura più adeguatamente considerando:
a) o le differenze fra ogni termine e un valore medio (cioè gli scostamenti o scarti);
b) o le differenze fra ciascun termine e tutti gli altri.
Di tali scarti o differenze si prende poi una media (per avere una sola misura sintetica della variabilità); bisogna però sempre trascurare i segni (altrimenti si avrebbe una compensazione fra differenze positive e negative); perciò si ricorre o ai valori assoluti o ai quadrati.
Noi studieremo precisamente:
a) lo scarto semplice medio (dalla media aritmetica o dalla mediana);
b) lo scarto quadratico medio s ( =sigma)
c) la differenza media assoluta.
E’ la media aritmetica degli scarti fra i singoli termini e la media aritmetica, presi in valore assoluto.
Se:
x1, x2, x3, …, xn
sono i dati (nel caso di una serie) e M è la loro media aritmetica, lo scarto semplice medio, che indicheremo con S, è dato da:
S= |x1 –M| +|x2 –M| + | x3–M| + …+ | xn–M|
n
Dati i numeri 3, 5, 10, 12, 15, lo scarto semplice medio è:
S= 6+4+1+3+6 =4
Tab. 1 Esempio di calcolo di S e s nel caso di una serie

Nel caso di una seriazione, bisogna fare naturalmente la media ponderata degli scarti.
Nella Tab. 1 è esposto il calcolo di S per la serie delle produzioni di frumento e nella Tab. 2 quello per la seriazione delle stature. Qui i singoli scarti sono moltiplicati per i relativi pesi (frequenze) e la somma dei prodotti va divisa per la somma dei pesi (popolazione).
Tab. 2 Esempio di calcolo di S nel caso di una seriazione

Un indice analogo è lo scarto semplice medio dalla mediana. Si tratta di fare la media aritmetica dei valori assoluti degli scarti dei singoli termini dalla mediana (anziché dalla media aritmetica).
Se Me è la mediana, si ha, sempre nel caso di una serie:
S’= |x1 –Me| +|x2 –Me| + …+ | xn–Me|
n
Nell'esempio della produzione di frumento, essendo Me = 94,10, si trova:
S’= 12,80 + 8,20 + 3,70 + + 2,80 = 93,3 = 4,665
20 20
Lo scarto semplice medio dalla mediana S' risulta non maggiore di quello S calcolato dalla media aritmetica, perché, come abbiamo detto parlando della mediana, questa ha la proprietà di rendere minima la somma (e quindi anche la media) dei valori assoluti degli scarti.
Per lo stesso motivo, se si calcolassero gli scarti rispetto a un altro valore qualunque, si otterrebbe sempre (come media degli scarti) un valore maggiore di S'.
Così lo scarto semplice medio rispetto a 85,9 (produzione del 1964), risulta:
= 173,9 =8,695 > 4,665
20
Si ottiene calcolando la media quadratica degli scarti s fra i termini e la loro media aritmetica; si fa cioè la media dei quadrati di tali scarti (*) e poi si estrae la radice quadrata. Lo scarto quadratico medio si indica di solito con la lettera greca s (sigma).
(*) La media dei quadrati degli scarti si dice varianza (s
Nel caso di una serie si ha dunque:

Per esempio, facendo riferimento ai soliti dati: 3, 5, 10, 12, 15 e tenendo presente che M= 9, si ha subito:
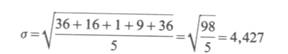
e nel caso di una seriazione, tenendo conto dei pesi:
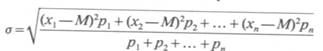
Nella Tab. 1 della lezione precedente è esposto il calcolo dello scarto quadratico medio per la serie delle produzioni di frumento; nella Tab. 3 che segue lo stesso calcolo è fatto per la seriazione delle stature.
Tab. 3 Esempio di calcolo s in una seriazione
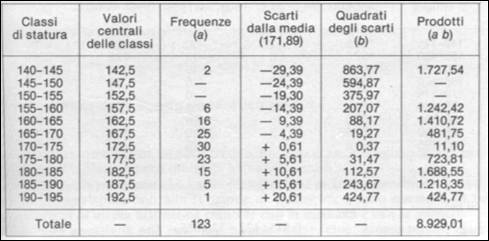
Le prime tre colonne riproducono la solita tabella. Dopo aver calcolato la media aritmetica, che è 171,89 si calcolano (col. 4) gli scarti fra i valori centrali delle classi e la media e nella colonna 5 i quadrati di essi.
Infine, per fare la media di tali quadrati,
nella col. 6 si calcolano i prodotti del quadrati per le frequenze. La somma di tali prodotti va divisa per la somma dei pesi.
Si ha:
Si deve infine estrarre la radice quadrata e si ha: s
Lo scarto quadratico medio riveste un'importanza fondamentale nella Statistica. Dobbiamo però limitarci a qualche cenno.
Abbiamo già ricordato che molte distribuzioni di frequenze danno luogo a curve che corrispondono alla funzione di Gauss; cioè sono normali.
In tali distribuzioni la media aritmetica coincide con la mediana e con la moda.
La curva gaussiana può però avere varie forme, cioè, grosso modo, essere più larga o più stretta. Ebbene, si può dimostrare che il valore di s determina la forma della curva e precisamente che M-s a e M+s o sono le ascisse dei due punti di flesso cioè di quei punti nei quali la curva cambia concavità.
Inoltre, si dimostra che, quando il carattere ha distribuzione normale, circa il 95% dei dati è compreso entro i limiti M-2s e M+2s e la quasi totalità dei dati è compresa entro i limiti M-3s e M+3s sicché solo eccezionalmente si hanno dati il cui scarto dalla media supera, in valore assoluto, s
Così, con i dati della tabella 3, abbiamo trovato M= 171,89, Q=8,52. Dato che ]a distribuzione è approssimativamente gaussiana, deve accadere che la quasi totalità degli iscritti abbia statura compresa fra:
171,89-3*8,52 e 171,89+3*8,52
cioè fra 146,33 e 197,45.
Di fatto, 2 soli (su 123) fanno eccezione, avendo statura inferiore a 145.
Le considerazioni precedenti (che dimostrano l'importanza dello scarto quadratico medio per quei fenomeni che hanno distribuzione normale) trovano una notevole applicazione per 1'interpretazione dei risultati di una rilevazione campionaria.
Se interessa determinare la media di un certo carattere in una popolazione (per es., in un'impresa che fabbrica dei pezzi in serie, il peso medio dei pezzi) e, per ragioni di economia, si limita l'indagine a un campione (scelto a caso), è ovvio che la media del campione non sarà necessariamente uguale a quella (che a noi interessa) dell'universo.
Infatti, dall'universo si possono estrarre moltissimi campioni diversi, relativamente ai quali la media può risultare diversa. Ora, si dimostra che, se noi considerassimo tutti i possibili campioni (per es. di 25 pezzi) che si possono estrarre dall'universo, e calcolassimo per ciascuno la media, avremmo con tali medie una distribuzione gaussiana (nell'ipotesi che la distribuzione dell'universo sia gaussiana), la cui media coincide con la media dell'universo, e il cui scarto quadratico medio (che indichiamo con vm, cioè v delle medie) si ottiene dallo scarto quadratico medio dell'universo con la relazione:
s M s
![]() [1]
[1]
dove n è il numero degli elementi del campione
(nel nostro esempio n = 25).
Esattamente si avrebbe:
s M s ![]()
![]() [1 bis]
[1 bis]
dove N è il numero degli elementi dell'universo. Se N è molto grande, il fattore sotto la seconda radice è molto prossimo a 1 e viene spesso trascurato. Ciò è poi necessario quando, come spesso avviene, N non è noto. Si usa allora senz'altro la prima formula su riportata.

La figura mostra (schematicamente) due distribuzioni gaussiane. La prima riguarda le intensità del carattere (peso) nei singoli individui (pezzi) dell'universo: la media è M e lo scarto quadratico medio è s La seconda riguarda l’intensità media nei singoli campioni di 25 elementi: la media è ancora M e lo scarto quadratico medio è:
s M s:![]() = s
= s
In pratica non è possibile costruire la seconda distribuzione, perché il numero dei campioni che teoricamente si potrebbero fare è grandissimo; anche la prima, del resto è, di solito, ignota. In pratica si ha soltanto un campione (di 25 elementi), di cui si calcola la media (sia per es. 34,81) e lo scarto quadratico medio (sia per es. 8,15). Si sostituisce questo valore di v a quello, ignoto, dell'universo, cioè della prima distribuzione, e con la formula [1] se ne deduce s M (cioè lo scarto quadratico medio della seconda distribuzione), che risulta:
s M ![]()
Ora, la media del campione (34,81) è uno dei valori della seconda distribuzione. Siccome sappiamo che in una distribuzione gaussiana solo eccezionalmente si hanno scarti maggiori in valore assoluto di 3s, possiamo essere quasi certi che il valore trovato (34,81) differisce dalla media (incognita) dell'universo per meno di 3 * 1,63 = 4,89, e che la media dell'universo è quindi compresa fra 34,81-4,89 e 34,81 +4,89, cioè fra 29,92 e 39,70.
Facciamo un secondo esempio, riferendoci alle stature già note della tabella 3. Mediante sorteggio abbiamo estratto, dall'universo di N=123 unità, un campione di n = 50 iscritti. Calcolandone la statura media , si trova il valore di cm 171,48. Poiché il valore di s M in base alla [1 bis], è di 0,9320, abbiamo teoricamente la quasi certezza che la statura media dell'universo sia compresa fra:
171,48 - 3 * 0,9320 e 171,48 + 3* 0,9320, cioè fra 168,68 e 174,276
Possiamo anche dire che c'è una probabilità del 95% che la statura media dell'universo cada nell'intervallo da 171,48-2*0,9320 a 171,48+2*0,9320 (cioè da 169,62 a 174,28 cm)
In realtà, la media per la statura è 171,89 , come abbiamo visto,.
E’ la media aritmetica di tutte le possibili differenze fra ogni termine e tutti gli altri, prese sempre in valore assoluto. Essa si indica con Δ (delta) ed è un indice assoluto di variabilità.
Se si hanno n termini, per calcolare le differenze bisogna considerare tutte le coppie, cioè tutte le disposizioni di n oggetti di classe 2.
Il loro numero è, come è noto:
Ma tali ultime differenze sono nulle, e quindi non aggiungono nulla alla somma delle differenze; contano soltanto come numero (e quindi al denominatore, nel calcolo della differenza media).
Indicando con D la somma di tutte le differenze (prese in valore assoluto) si hanno quindi due differenze medie:
a) la differenza media semplice che è:
D
n(n -
b) la differenza media con ripetizione che è:
R D
n2
[2]
e naturalmente risulta minore di Δ
Il calcolo diretto della differenza media è agevole solo se i dati sono pochi
Così, per i soliti 5 numeri 3, 5, 10, 12, 15, si ha il seguente quadro di differenze:
|
|
|
|
|
|
|
|
|
|
|
|
|
-12 |
|
|
|
|
|
|
|
|
|
|
|
I cui valori assoluti sono: 2, 7, 9, 12, 2, 5, 7, 10, 7, 5, 2, 5, 9, 7, 2, 3, 12, 10, 5, 3.
La somma delle differenze è: D= 124. Quindi la differenza media semplice e quella con ripetizione sono rispettivamente pari a:
Δ
52
Ma quando i dati sono numerosi o si ha una seriazione, il calcolo stesso diventa molto faticoso. Vi sono, però, dei procedimenti semplificativi, di cui (omettendo la dimostrazione) mostreremo il pratico uso nel caso di una serie e nel caso di una seriazione.
Premettiamo che
si dice distanza graduale il numero degli intervalli che separa due termini.
Ora, per calcolare la somma D delle differenze, nel caso di una serie, si trascrivono i dati prima in ordine crescente, poi in ordine decrescente; si fa la differenza in valore assoluto fra i termini corrispondenti delle due successioni e la si moltiplica per la distanza graduale dei due termini stessi; la somma di tali prodotti, dà D
Nella seguente Tab. 5 è esposto il procedimento di calcolo della differenza media per i dati della Tab. 4.
Tab. 4 Produzione del frumento in Italia dal 1963 al 1982 (milioni di quintali)

Tab. 5 Esempio di calcolo della differenza media, nel caso di una serie

Ecco come si è proceduto al calcolo delle distanze graduali (4a colonna): nella prima riga, sono considerati il 1° termine e l'ultimo, cioè il 20°: il numero degli intervalli che li separano è perciò 19; così nella seconda riga si considerano il 2° termine e il 19° e la distanza graduale è 17; e così via.
La somma dei prodotti è:
D
e, poiché n = 20:
Δ
20*19
ΔR=
202
Sostanzialmente analogo, anche se un po' più complicato, è il calcolo nel caso di una seriazione.
Facciamo vedere (Tab. 6) come si dispongono praticamente i calcoli per ottenere la differenza media nel caso di una seriazione relativa alla distribuzione di un gruppo di redditieri secondo il reddito posseduto. I dati sui quali dobbiamo effettuare il calcolo sono quelli delle prime due colonne. Gli altri indicano ordinatamente le operazioni da eseguire.
Tab. 6 Esempio di calcolo della differenza media, nel caso di una seriazione

Nelle colonne 5 e 6 sono sommate dall'alto al basso e dal basso all'alto le frequenze della col. 2. Nella col. 7 figurano le differenze fra le col. 5 e 6 (con segno). Infine nella col. 8 vi sono i prodotti dei valori delle col. 4 e 7.
La somma dei prodotti, raddoppiata, dà D; per calcolare le differenze medie nelle [1] e [2] bisogna prendere naturalmente n =100 (somma delle frequenze).
Si ha:
Δ = 13,228 (milioni)
ΔR = 13,096 (milioni)
Osservazione - Il prodotto della frequenza per il valore centrale dà, in ogni classe (in via approssimata), il reddito totale delle persone comprese in quella classe. Talvolta la rilevazione dà già l'importo esatto di questi redditi totali, basta allora moltiplicare questo importo per le differenze della col. 7 (e non servono i valori centrali).
Tutti gli indici di cui abbiamo sinora parlato si dicono assoluti di variabilità: la loro caratteristica è di essere espressi nella stessa unità di misura in cui sono espressi i dati.
Così, nel caso delle stature (che sono espresse in cm), sia il campo di variazione, che gli scarti medi (semplice e quadratico) e la differenza media sono espressi in cm.
Ora questi indici sono facilmente interpretabili, ma non sono molto adatti per confrontare la diversa variabilità di fenomeni diversi.
Così, se si calcola lo scarto quadratico medio per le stature degli iscritti di leva e per i perimetri toracici degli stessi, si trova che il primo è cm 8,52 e il secondo cm 7,27; ma non si potrebbe senz'altro dire che le stature presentano una variabilità maggiore dei perimetri toracici, perché le stature si aggirano sui 170 cm e i perimetri toracici su 80.
Se poi si calcolasse lo stesso indice, per es., per il peso corporeo degli iscritti, si avrebbe un indice in kg assolutamente non confrontabile coi precedenti.
Sorge perciò l'idea di calcolare degli indici di variabilità relativi, che siano numeri puri (senza unità di misura), e che permettano il confronto della variabilità anche fra fenomeni diversi.
Essi si ottengono dividendo gli indici di variabilità assoluti per un'intensità; di solito per una media delle intensità.
Si ha così un rapporto fra due grandezze omogenee, che è un numero puro.
Di regola si divide l'indice assoluto per la media aritmetica, e si hanno così principalmente:
a) lo scarto medio relativo dalla media aritmetica
S
M
b) lo scarto quadratico medio relativo
s
M
Tab. 7 Distribuzione secondo la statura di un gruppo di iscritti di leva

Così, per i dati delle Tab. 4 (produzione frumento) e 7 (stature), si ha:
Produz. frumento Stature
M 91,68 (milioni di q) 171,89 (cm)
S 4,962 (milioni di q) 6,59 (cm)
s (milioni di q) 8,52 (cm)
S 0,0551 0,0383
M
s 0,0835 0,0496
M
Dagli indici relativi risulta che la variabilità della produzione del frumento è maggiore di quella delle stature, mentre nessun confronto era possibile mediante gli indici assoluti.
Altri indici relativi di variabilità si ottengono dividendo un indice assoluto per il massimo valore che esso può assumere.
L'indice relativo è allora certamente non maggiore di 1, ed è più agevole interpretarlo anche da solo (per ES. valore 0,2 indicherà poca variabilità e il valore 0,9 molta variabilità).
Così, si può dimostrare che:
a) lo scarto quadratico medio è sempre minore (o al più uguale) della media quadratica;
b) lo scarto semplice medio dalla mediana è sempre minore (o al più uguale) della mediana;
c) la differenza media semplice è sempre minore del doppio della media aritmetica.
Pertanto si possono proporre i seguenti indici relativi di variabilità (che non superano mai il valore 1):
a) il rapporto fra scarto quadratico medio e media quadratica;
b) il rapporto fra scarto semplice medio dalla mediana e mediana;
c) il rapporto fra la differenza media semplice e il doppio della media aritmetica
In pratica solo quest'ultimo è usato e prende il nome di rapporto di concentrazione; ne parleremo diffusamente nella prossima lezione.
 |
| Appunti su: |
|
| Appunti Fisica |  |
| Tesine Contabilita |  |
| Lezioni Geografia |  |